В статье описана процедура создания новой компонентной технологии математического моделирования в электронных таблицах.
Ключевые слова: компонентная модель, формальная логика, макрос.
Технология компонентного табличного моделирования основана на алгоритме решения исходной задачи и включает ряд процедур [1]:
− анализ предметной области, включающий операции структуризации словесного описания проблемы, постановки задачи, формулировки целей моделирования;
− процедура формализации задачи моделирования, содержит операции задания входов, выходов и показателей эффективности; построения причинно-следственных диаграмм; объявление переменных модели; разработки алгоритма решения задачи;
− процедура создания компонентной табличной модели, включает операции выбора из библиотеки компонентов, необходимых для решения задачи; задания информационных связей между компонентами, настройку параметров компонентов;
− процедура интерпретации результатов моделирования, содержащая операции планирования модельного эксперимента, анализа модели и интерпретации полученных результатов.
Для создания компонентных табличных моделей, прежде всего, необходимо открыть рабочую книгу Microsoft Excel на основе шаблона, содержащего библиотеку компонентов формальной логики. Затем нужно открыть библиотеку компонентов и, выделив область необходимого компонента, скопировать его в буфер обмена (Ctrl+C) (рис. 1).
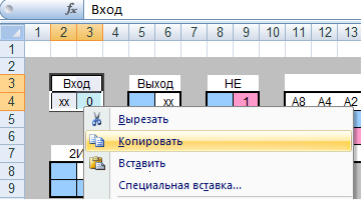
Рис. 1. Копирование блока библиотеки в буфер обмена
На лист рабочей книги Excel вставляем скопированный блок (Ctrl+V). Аналогичным образом добавляются остальные блоки создаваемой модели. Затем позиционируем компоненты на рабочем поле и устанавливаем связи между блоками согласно реализуемой комбинационной схеме (модели).
Так, например, для установки связи между компонентами логической схемы «Вход» и «НЕ», в входной ячейке блока «НЕ» вводим знак равенства «=» и выделяем выходную ячейку блока «Вход» (рис. 2), затем нажимаем клавишу Enter.
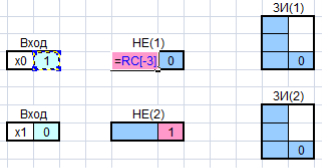
Рис. 2. Установление связей между ячейками
Теперь входная ячейка блока инверсии будет равна значению выбранного входного значения схемы.
По завершению установления связей, в последнем блоке отображается окончательный результат. Теперь, при смене входных значений, можно наблюдать изменение выходной ячейки.
Для компонентов формальной логики технология создания модели аналогична: блоки библиотеки копируются, добавляются на лист рабочей книги, позиционируются и устанавливаются связи между блоками (рис. 3).
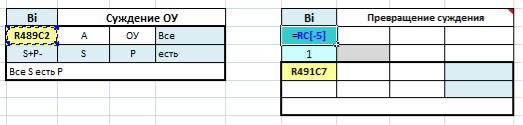
Рис. 3. Пример создания модели формальной логики
Далее в блоках формальной логики при необходимости изменяются имена терминов суждений и значения субъекта и предиката, а также распределенности терминов при помощи ниспадающих списков блоков.
Для визуализации связей между ячейками создадим макрос, отображающий эти связи при помощи графических стрелок. Для этого при помощи графических инструментов создаем три кнопки, выполняющие отображение зависимостей между зависимыми ячейками, а также кнопку по удалению стрелок, отображающих данные зависимости (рис. 4).

Рис. 4. Кнопки визуализации связей между ячейками
Для каждой кнопки создаем макрос. Для этого в редактор Visual Basic для кнопки «Влияющие ячейки» задаем код:
Sub Precendents()
Dim i As Integer
Dim n As Integer
n = 10
For i = 1 To n
Selection.ShowPrecedents
Next
End Sub
Для кнопки «Зависимые ячейки» используем код:
Sub Dependents()
Dim i As Integer
Dim n As Integer
n = 10
For i = 1 To n
Selection.ShowDependents
Next
End Sub
Для кнопки удаление стрелок связей присваиваем код:
Sub ArrowsDelete()
ActiveSheet.ClearArrows
End Sub
Теперь, когда выделяется любая ячейка на листе Excel, при нажатии кнопки «Влияющие ячейки» и «Зависимые ячейки» (рис. 5), отобразятся стрелки связи, а при нажатии кнопки «Убрать стрелки» стрелки соответственно удалятся.
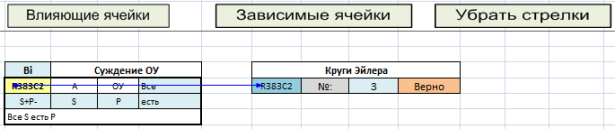
Рис. 5. Использование кнопки «Влияющие ячейки»
Таким образом, в настоящей публикации представлена разработанная технология компонентного табличного моделирования.
Литература:
1. Игошин В. И. Математическая логика и теория алгоритмов [Текст]: учеб. пособие для студентов высш. учеб. заведений. — М.: Академия, 2008. — 448 с.

