В статье рассматривается разработка математической модели многомерного объекта управления в условиях нестационарности. Предложена компактная векторно-матричная форма записи модели, позволяющая автоматизировать этап дискретного динамического описания объекта независимо от количества технологических параметров.
Ключевые слова: многомерный объект управления, система управления, дискретная математическая модель, разностные уравнения.
Создание адекватной математической модели технологических объектов во многом определяет эффективность их последующего управления не только на стадии создания систем управления, но и на стадии последующей эксплуатации. Традиционные методы классической теории управления основываются на предположении, что математическая модель объекта является известной и абсолютно точно описывает его поведение [1]. Однако использование таких методов для реальных промышленных многомерных объектов управления в условиях существенной неопределенности дают плохие результаты, поскольку их некоторые характеристики заранее неизвестны или существенным образом изменяются в процессе функционирования [2].
Структурная схема, отражающая топологию физических связей многомерного объекта управления (ОУ), содержащего r входов и выходов при наличии w внешних возмущений, представлена на рисунке 1.
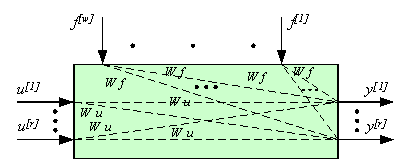
Рис. 1. Структурная схема r -мерного ОУ при наличии w внешних возмущений
Математическое представление дискретной модели может быть представлено [2]:
— в переменных вход-выход;
— в переменных состояния;
— в виде структурных схем;
— в виде разностных уравнений.
Описание методом «вход-выход» используется только для линейных детерминированных систем. Метод в переменных состояния применим для многомерных линейных систем, и заключается в описании модели в виде матрицы величин. Для многомерных динамических ОУ наиболее полной и наглядной является запись модели с помощью системы разностных уравнений:
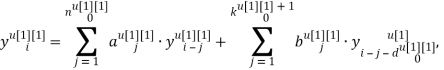

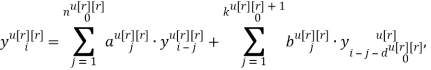
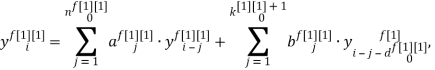

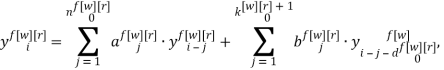
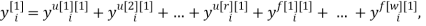

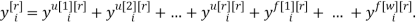
Универсальную запись разностного уравнения для дискретной модели объекта на основе переменной индексации можно представить следующим образом:
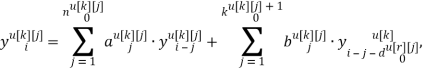
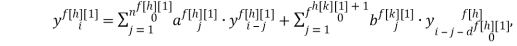
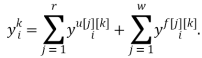
Применим прямое преобразование, используя оператор сдвига z для системы разностных уравнений (2) [3]. Тогда модель ОУ с использованием дискретных передаточных функций запишется в виде:
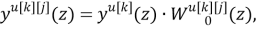
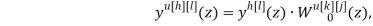
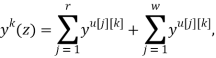
где
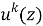
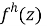
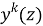
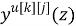
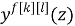
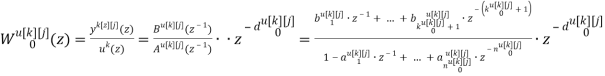
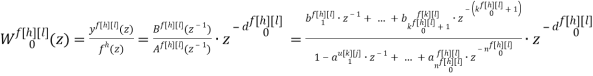
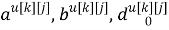
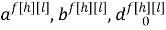
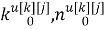
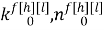
k
,
j
,
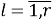
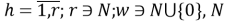
Скалярные формы записи модели, представленные системами уравнений (1)-(3), ввиду их громоздкости вызывают существенные трудности при последующем этапе синтеза многосвязной оптимальной цифровой системы управления. Поэтому воспользуемся более компактной векторно-матричной формой:
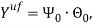
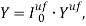
где
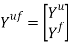
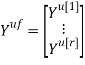
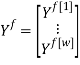
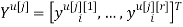
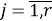
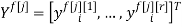
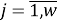
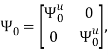
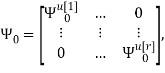
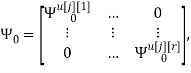
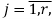
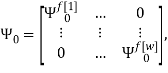
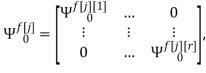
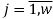
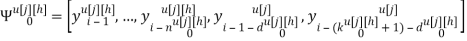
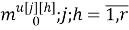
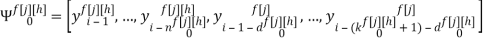
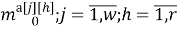
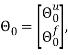
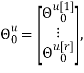
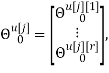
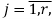
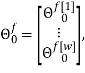
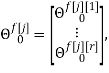
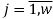
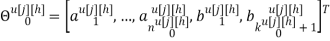
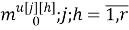
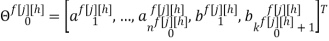
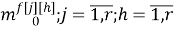
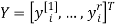
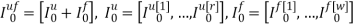
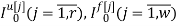
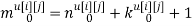
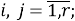
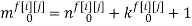
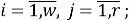
r — размерность ОУ, т.е. число управляемых величин;
w — число внешних контролируемых возмущающих воздействий.
Использование разработанной модели многомерного ОУ (4), учитывающей наличие r входов и выходов и w возмущающих воздействий, позволяет автоматизировать этап составления его дискретного динамического описания независимо от количества и структуры взаимосвязей технологических параметров. При этом разработчику необходимо лишь указать размерность объекта по входам, выходам и возмущениям, в результате чего будет получена его математическая модель, в которой останется определить в ходе идентификации только порядки и параметры разностных уравнений, описывающих отдельные каналы.
Литература:
- Никифоров В. О., Слита О. В., Ушаков А. В. Интеллектуальное управление в условиях неопределенности: учебное пособие. — СПб: СПбГУ ИТМО, 2011. — 226 с.
- Дилигенская А. Н. Идентификация объектов управления: учебное пособие. — Самара: СГТУ, 2009. — 135 с.
- Масленников А. Дискретные системы автоматического управления: конспект лекций. — Москва, 2019. — 257 с.

