В статье описан процесс разработки и создания собственного логического калькулятора, позволяющего решать типовые задачи математической логики.
Ключевые слова: логический калькулятор, математическая логика, таблица истинности, логическая формула, равносильность формул, логическое следствие.
Ценность изучения математической логики студентами математических направлений вузов не подвергается сомнению. Глубина изучения такого курса может варьироваться, но существует ряд типовых задач, без знания которых невозможно решать более серьезные проблемы. К таковым отнесем построение таблицы истинности, определение класса формулы, приведение логических выражений к совершенной дизъюнктивной нормальной форме (СДНФ) и совершенной конъюнктивной нормальной форме (СКНФ), проверку равносильности двух формул и правильности логического следования [1].
Логические калькуляторы — важнейшие инструменты для обработки логических выражений и решения сложных задач, связанных с логикой. Они широко применяются в различных областях, включая математику, философию, информатику, электронику и другие.
По условию, задание предполагает создание приложение и написание программного кода, который будет обрабатывать введенное пользователем логическое выражение и выводить соответствующий результат в зависимости от требований.
Определив основные задачи математической логики, заметим, что все они могут быть решены с помощью анализа таблицы истинности заданной формулы, а значит, эта задача хорошо поддается алгоритмизации. Следовательно, разработка логического калькулятора является удачной возможностью для студента продемонстрировать свои знания в области математики и умения в программировании. Создание логического калькулятора — задача не новая [2], но каждый исполнитель может решить ее по-своему, найдя иные подходы к определению круга рассматриваемых математических задач или используя другие средства программирования и возможности выбранных платформ.
На первом этапе исследований необходимо определить все используемые параметры для анализа формулы и искать возможности их перевода в программный код. Сразу же возникает вопрос о формате хранения и обработки указанного пользователем выражения.
Полученное выражение хранится в переменной строкового типа string. Таблица истинности для введенного логического выражения должна строиться универсальной, вне зависимости от сложности выражения и количества операций и операндов в нем. Для этого данная строка изучается с помощью вложенных условных операторов, откуда становится известно о количестве операндов и операций, входящих в данную логическую формулу.
Одной из ключевых проблем при вычислении значения логической формулы стал приоритет логических операций и необходимость правильного использования скобок. Например, когда пользователь видит логическое или математическое выражение с разными уровнями вложенных скобок, он интуитивно понимает, что нужно начинать вычисления с самых «глубоких» скобок. Однако написание такой программы, которая эффективно вычисляет подобное выражение с точки зрения затрачиваемых времени и памяти, задача не из легких. Для этого был реализован метод обратной польской нотации.
Обратная польская нотация (ОПН), также известная как постфиксная нотация, — это способ записи математических и логических выражений, в котором операнды предшествуют своим операторам [3].
В ОПН порядок выполнения операций однозначно определяется последовательностью элементов, без необходимости использования скобок. Это устраняет возможность неправильного интерпретирования выражений и повышает четкость их выполнения. Выражения в ОПН легче вычислять, так как операции выполняются сразу над операндами, без необходимости учитывать приоритеты операций или расставлять скобки. Это упрощает алгоритмы обработки выражений и ускоряет процесс вычислений.
Для перевода выражения в ОПН для хранения информации используется стек. Рассматриваемая логическая формула состоит из
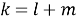
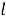
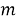
Изначально формула записывается в инфиксной форме (двуместная операция находится между операндами
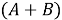
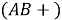
Применение ОПН удобно для компьютерных программ, поскольку не требует использования дополнительного стека для хранения операций и операндов при расстановке скобок. Это позволяет снизить нагрузку на память и упрощает реализацию алгоритмов вычисления.
Написание программы было решено осуществить в свободной среде разработки (IDE) Qt Creator, так как в ней есть возможность создания удобного для пользователя интерфейса приложения логического калькулятора с различными кнопками и виджетами [4].
Код программы организован посредством связанных между собой функций. Каждая функция имеет особую роль и отвечает за определенную опцию в программе. Главной функцией является функция main для получения от пользователя логической формулы, её преобразования, а также для построения таблицы истинности. Остальные функции основываются на результате работы функции main.
Программа содержит 3 основные функции для определения равносильности двух формул, проверки на верность логического следования и различные вычисления по таблице истинности (тип формулы, построение СКНФ, СДНФ). Основная задача каждой из этих функций — формирование таблицы истинности. Но, в зависимости от условия задачи, таблица истинности формируется по-разному.
Например, для различных вычислений по таблице истинности для логической формулы, содержащей n пропозициональных переменных, таблица строится стандартным образом: первые n столбцов — все уникальные переменные, входящие во введенную логическую формулу, затем добавляется еще один столбец, содержащий итоговое значение формулы для каждого набора всевозможных значений логических переменных.
Для определения равносильности двух формул таблица истинности строится аналогичным образом: первые n столбцов — уникальные переменные, затем добавляется еще два столбца в таблицу для итоговых значений двух формул, равносильность которых подлежит проверке.
Таблица истинности для проверки на правильность логического следования некоторого заключения из k посылок строится несколько иначе. Неизменными остаются первые n столбцов, содержащие уникальные переменные. После этого добавляется еще k+ 1 столбец, в котором находятся значения k посылок и значение одного заключения.
В программе имеются десять дополнительных функций, каждая из которых отвечает за определенное действие (проверка на корректность введенной формулы, вычисление таблицы истинности, определения типа формулы и другие). Также код программы содержит четыре вспомогательные функции для задания приоритета логических операций и проверки символа на принадлежность к латинскому алфавиту, которые вызываются в основных программах.
При запуске программы в QT Creator открывается главное окно — приложение логического калькулятора. Оно включает в себя все необходимые кнопки, к которым подключены описанные выше функции (обработчики событий, активирующиеся при нажатии на соответствующую кнопку). Интерфейс программы интуитивно понятен, поэтому не требует детального описания. Внешний вид главного окна программы логического калькулятора продемонстрирован на рис. 1.
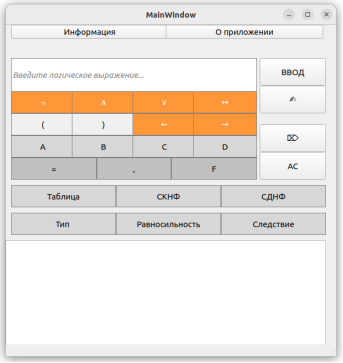
Рис. 1. Интерфейс приложения
При запуске программы автоматически подсвечивается окно для ввода логической формулы. Пользователю предлагается ввести формулу, содержащую до четырех переменных, с помощью кнопок в приложении. Однако есть возможность ввода формулы с клавиатуры, что увеличивает максимальное количество используемых переменных до 52 букв латинского алфавита (латинские буквы верхнего и нижнего регистра). Также логическую формулу можно ввести с помощью текстового файла, записав в него формулу согласно инструкции, или же скопировать и вставить нажатием правой кнопкой мыши по окну ввода.
Программа может обрабатывать шесть логических операций (инверсия, конъюнкция, дизъюнкция, импликация, репликация, эквивалентность) причем их приоритетность соответствует порядку следования операций в формате чтения (слева направо). Следует отметить, что пользователь имеет возможность изменять приоритетность при необходимости, используя скобки.
Для отладки программы были разработаны примеры, тестирующие ее в тех ситуациях, в которых предполагается наличие ошибок. При обнаружении сбоев были внесены необходимые корректировки в код программы, после чего производилось повторное тестирование. Результаты тестирования подтвердили, что алгоритмы программы устойчивы к различным входным данным и правильно решают логические задачи в соответствии с заданными условиями. Рассмотрим некоторые примеры работы программы.
Для функции, отвечающей за построение таблицы истинности примером проверки корректной работы является введенная логическая формула, в которой находятся переменные без каких-либо логических операций. В данном случае при попытке нажатия на кнопку «Ввести» отобразиться новое окно с предупреждением, показанное на рис. 2.
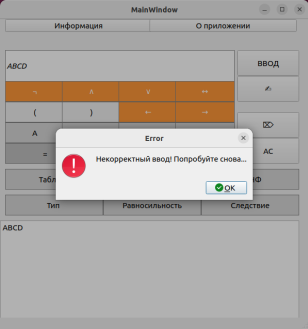
Рис. 2. Демонстрация некорректного вода формулы
Рис. 3. Демонстрация корректного вода формулы
При тестировании функции проверки равносильности двух логических формул для выявления конфликтных ситуаций было принято решение использовать для проверки на равносильность две похожие логические формулы, различающихся в одной логической операции.
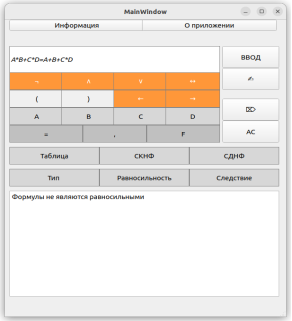
Рис. 4. Демонстрация проверки равносильности формул
Как и ожидалось, программа выдает корректный результат, так как то, что для человеческого взгляда может показаться похожим и, в случае ошибки, идентичным, для запрограммированного алгоритма является абсолютно разным.
Пример работы программы для равносильных формул продемонстрирован на рис. 5.
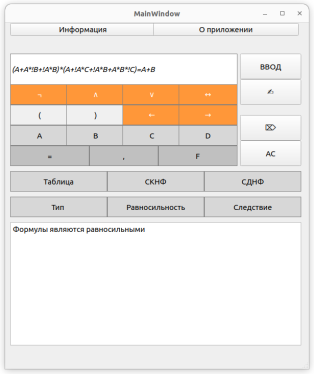
Рис. 5. Демонстрация проверки равносильности формул
Тестирование функции проверки верности логического следования представлено на рис. 6.
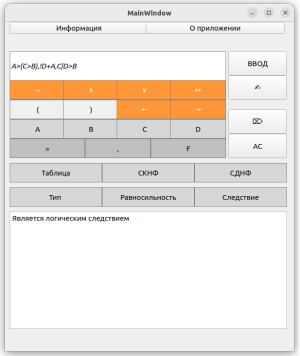
Рис. 6. Демонстрация верного логического следования
Определение типа формулы представлено на рис. 7.
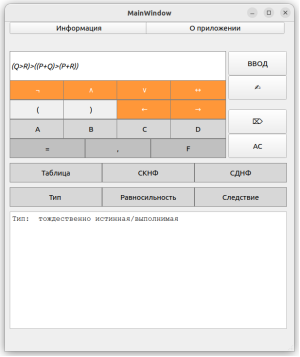
Рис. 7. Демонстрация определения типа формулы на примере тавтологии
Тестирование функции построения СДНФ было принято осуществить на двух примерах: в случае, когда СДНФ существует и когда её не существует для данной логической формулы.
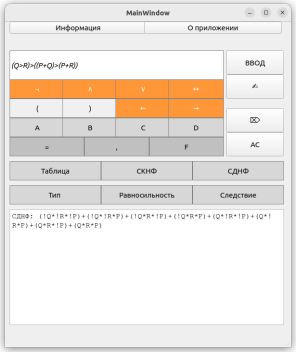
Рис. 8. Демонстрация построения СДНФ для тавтологии
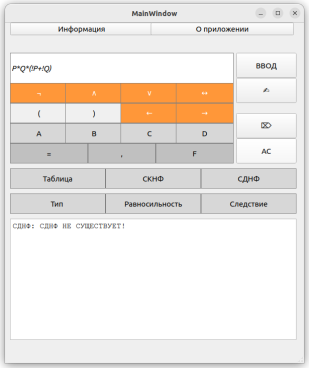
Рис. 9. Демонстрация построения СДНФ для противоречия
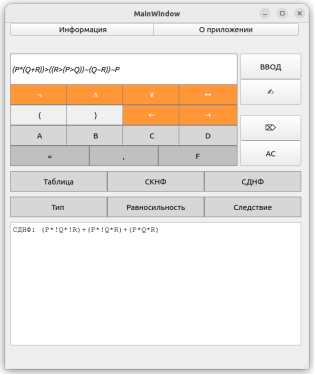
Рис. 10. Демонстрация построения СДНФ для выполнимой/опровержимой формулы
Аналогичным образом была протестирована функция, результатом которой является вычисленная СКНФ для введенной логической формулы.
Для анализа быстродействия программы логического калькулятора была проведена серия экспериментов с различным количеством уникальных переменных. В каждом эксперименте измерялось время вычисления в программе на примере построении таблицы истинности конъюнкции всех уникальных переменных. Результаты измерений приведены в таблице 1.
Таблица 1
Время работы программы

Из таблицы видно, что время выполнения программы увеличивается с ростом количества уникальных переменных. Это ожидаемое поведение, так как большее количество переменных требует дополнительных вычислений.
Таким образом, программа работает для выражения любой сложности. Нет ограничения на количество операций и повторения операндов. Скорость вычисления программы напрямую зависит от количество уникальных операндов, так как количество строк в таблице истинности (т. е. вычислений в таблице) вычисляется по формуле
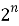
Для учебных целей, как правило, достаточно 3–5 уникальных операндов. Для такого количества вычислений таблицы истинности программа работает достаточно быстро, поэтому является удобной в использовании. Более того, даже при увеличении количества уникальных операндов, использование эффективных алгоритмов программы позволяют поддерживать приемлемую производительность. Это делает её подходящей не только для учебных, но и для исследовательских целей, где требуется обработка более сложных логических выражений.
Литература:
1. Иванисова, О. В. Дискретная математика и математическая логика: учебное пособие / О. В. Иванисова, И. В. Сухан — М.; Берлин: Директ-Медиа, 2020.
2. Чалыкина, Е. Г. Разработка и конструирование логического калькулятора / Е. Г. Чалыкина, И. В. Сухан. — Текст: непосредственный // Молодой ученый. — 2018. — № 20 (206). — С. 39–44.
3. Обратная польская нотация: простое объяснение и практическое применение. — Текст: электронный: [сайт]. — URL: https://nauchniestati.ru/spravka/obratnaya-polskaya-notacziya/ (дата обращения: 09.02.2024).
4. Алексеев, Е. Р. Программирование на языке С++ в среде Qt Creator: учебное пособие / Е. Р. Алексеев, Г. Г. Злобин, Д. А. Костюк [и др.]. — М.: ALT Linux, 2015.

