Существуют различные методы решения задач теории вероятностей. Решение задач при помощи стандартных формул теории вероятностей (формулы сложения/умножения вероятностей/условной вероятности/ Байеса/ полной или не полной вероятности), решение методом перебора (при решении простых базовых задач), при помощи формул комбинаторики (сочетание, размещение, перестановки и т. д.), а также при помощи математического аппарата теории графов. Есть ряд задач, которые можно решить, используя разные подходы по отдельности либо их комбинацию.
Ключевые слова: математический аппарат теории графов, решение задач теории вероятности, комбинаторика.
There are various methods for solving problems of the theory of probability. Solving problems using standard formulas of the theory of probability (formulas for adding / multiplying probabilities, conditional probability, Bayesian, total or incomplete probability), solving by brute force (when solving simple basic problems), using combinatorial formulas (combination, placement, permutations, etc.) and also with the help of the mathematical apparatus of graph theory. There are a number of problems that can be solved using different approaches individually or a combination of them.
Основной целью данной работы является построение и анализ алгоритма обучения школьников решению задач теории вероятностей с использованием теории графов.
Для достижения поставленной цели необходимо разработать алгоритм обучения школьников представлению задач теории вероятности в виде графа.
С каждым годом идет ужесточение правил проведения различных проверочных тестов, таких как ГИА, ЕГЭ, ВПР, ВКР для школьников. Используются все более сложные задачи (в том числе и по теории вероятностей), работы пишутся под камерами, что создает дополнительное давление на моральное состояние учеников. Кроме того, проверочные работы пишутся не по одному предмету. Даже способные ученики иногда не выдерживают давления и на экзаменах теряются, не могут вспомнить необходимые формулы. В связи с чем важно научить школьников решать задачи разными методами, что может пригодиться в сложной ситуации на экзамене. При решении задач по теории вероятностей наиболее запоминающимся для школьников является математический аппарат теории графов. Он не требует особых знаний и навыков, интуитивно понятен и позволяет решить некоторые сложные задачи по теории вероятностей.
Для решения задач теории вероятностей с использованием математического аппарата теории графов необходимо обладание базовым уровнем знаний в области теорий графов [1] и теории вероятностей [2–3] (навыки представления условий задачи в виде графа, понимание и навыки применения теорем сложения и умножения вероятностей, определение зависимости или независимости событий и т. д.). При большом количестве возможных исходов необходимо внимательно учесть все возможные варианты и правильно применить навыки сложения, умножения вероятностей.
Рассмотрим алгоритм обучения школьников на примере задачи про ковбоя Джона, стреляющего в муху (одна из задач, встречающихся в ЕГЭ).
Задача 1. Ковбой Джон попадает в муху на стене с вероятностью 0.9, если стреляет из пристрелянного револьвера. Если револьвер Джона не пристрелян, то он попадает в муху с вероятностью 0.2.
На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Алгоритм решения задачи 1 при помощи применения теории графов:
1 шаг: Выделить исходные данные, необходимые для решения поставленной задачи.
2 шаг: Обозначить базовыми формулами теории вероятности исходные данные, что нужно найти в итоге.
3 шаг: Схематически отобразить возможные варианты развития событий в виде графа.
4 шаг: Провести расчеты для получения недостающих данных
5 шаг: Решить задачу используя тривиальные формулы теории вероятностей.
Решение задачи:
1 шаг: в данной задаче все указанные данные будут использованы для решения.
2 шаг: Дано по условиям задачи:
Гипотеза Н 1 ‒ Джон стреляет из пристрелянного револьвера.
Гипотеза Н 2 ‒ Джон стреляет из непристрелянного револьвера.
Событие А: Попал в муху.
Событие В: Не попал в муху.
Условная вероятность Р(А|Н 1 ) ‒ Если револьвер пристрелянный, то Джон попадает в муху с вероятностью 0,9.
Условная вероятность Р(А|Н 2 ) ‒ Если револьвер непристрелянный, то Джон попадает в муху с вероятностью 0,2.
Необходимо найти: Р(В).
3 шаг: схематическое отображение возможных вариантов развития событий представлено на рисунке 1.
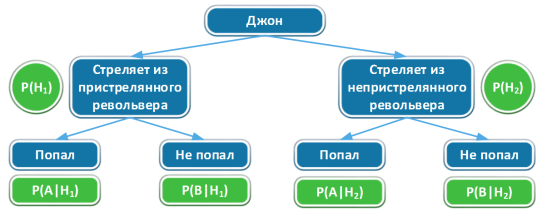
Рис. 1. Схематическое отображение возможных вариантов развития событий Задачи 1
4 шаг: из указанных исходных данных, можно найти вероятности реализации гипотез H 1 и H 2 , значения условных вероятностей Р(В|H 1 ), Р(В|H 2 ) [2–3].
P (H 1 ) = 0,4 (4 пристрелянных из всего 10 револьверов);
P (H 2 ) = 0,6 (6 непристрелянных из всего 10 револьверов);
Р(В|H 1 ) = 0,1 (Поскольку сумма вероятностей противоположных событий равна 1, а вероятность события Р(А|H 1 ) = 0,9, значит, Р(В|H 1 ) = 1–0,9 = 0,1);
Р(В|H 2 ) = 0,8 (По аналогии с Р(В|H 1 )).
5 шаг: схематическое отображение возможных вариантов развития событий с рассчитанными вероятностями представлено на рисунке 2.
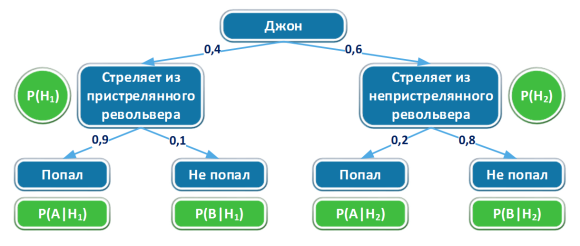
Рис. 2. Схематическое отображение возможных вариантов развития событий Задачи 1 с рассчитанными вероятностями
Для решения данной задачи достаточно знания формул сложения и умножения вероятностей, понимания зависимые события или нет, совместные или нет.
Решение задачи интуитивно понятно даже для школьника: для того, чтобы Джон не попал в муху из пристрелянного револьвера ему необходимо было взять пристрелянный револьвер, значит данные события зависимы, аналогично для непристрелянного револьвера. Джон мог не попасть как из пристрелянного ружья, так и из непристрелянного (наступление одного события исключает наступление другого, поскольку он стрелял либо из пристрелянного, либо из непристрелянного — события несовместные), следовательно, полная вероятность события В, что Джон не попал в муху вычисляется следующим образом:
Р(В) = P (H 1 ) *Р(В|H 1 ) + P (H 2 ) * Р(В|H 2 ) =0,4*0,1+0,6*0,8 = 0,52.
Таким образом, разбирая задачу теории вероятностей используя представление данной задачи в виде графа, школьник при помощи базовых знаний сможет решить задачу на априорную и апостериорную вероятность, делая очевидные логические заключения, что может пригодиться школьнику в критической ситуации на экзамене (если забудет формулу Байеса).
Разумеется, существует еще много различных задач теории вероятностей, которые встречаются в тестовых заданиях ЕГЭ или на олимпиадах. Однако нельзя рассмотреть их все в рамках одной статьи. Разработанный алгоритм является универсальным — применим для решения различных видов задач теории вероятностей.
Литература:
1 Оре О. Графы и их применение: Пер. с англ. 1965. 176 с.
2 В. С. Зарубин, А. П. Крищенко Теория вероятностей: Учебник. Изд. 4-е. Москва МГТУ им Н.Э Баумана, 2006.- 455с.
3 Гнеденко Б. В. Курс теории вероятностей: Учебник. Изд. 8-е, испр. и доп. — М.: Едиториал УРСС, 2005. — 448 с.

