Визуализация комбинаторных задач теории вероятностей



Визуализация комбинаторных задач теории вероятностей

Комбинаторные способы рассуждения занимают особое место в общей структуре научного мышления, поэтому требования к уровню комбинаторно-вероятностного мышления учащихся значительно выше, чем было ранее.

Эмпирическое исследование показало, что становление комбинаторного мышления у младших школьников и подростков в трех типах условий: стихийное развитие, школьное обучение, целенаправленное формирование, раннее визуальное стимулирование комбинаторного мышления благотворно сказывается как на умственном развитии детей в целом, так и в формировании образного мышления и даже развитии способностей к самостоятельной работе [1, с. 1], независящих от общей успеваемости в школе при традиционном обучении. Однако попытки включения комбинаторики в школьный курс математики в нашей стране не привели к успеху [2, с. 1]. Математики и педагоги столкнулись с трудноразрешимым противоречием: в начальной школе вводить комбинаторно-вероятностные понятия рано из-за недостатка необходимой «логической базы», а также соответствующего математического аппарата (дроби), а в старших классах вводить их оказывается уже поздно, потому что в этом возрасте математику преподают с обязательным использованием формализации знаний — материал сразу подается в виде сжатых математических формул, что не способствует улучшению понимания у школьников. По мнению многих детских психологов, это препятствие может быть преодолено при помощи введения дополнительного графического материала, упрощающего понимание математических формул младшими школьниками.

Значимость комбинаторики не ограничивается математическим знанием, потому что в ее основе лежит способность обучаемого определять, рассматривать и учитывать все возможные варианты сочетания каких-либо признаков или событий, являющейся предпосылкой логически полноценного рассуждения. По мнению Ж. Пиаже и Б. Инельдер [3, с. 263], специфика логики на этой стадии состоит не столько в том, что, освобождаясь от необходимости в конкретной предметной опоре, она реализуется как вербальная логика, а в том, что она начинает учитывать все возможные мыслимые комбинации. Экспериментально было выявлено, что способность детей комбинировать факторы и анализировать результаты их взаимодействия возникает достаточно поздно — лишь в подростковом возрасте и даже позднее. При этом самостоятельно приобретаемые подростками комбинаторно-вероятностные представления не совершенны и носят интуитивный характер.

Исследования показали, что и при специальном обучении только небольшая часть учеников средних общеобразовательных школ овладевает умением проводить комбинаторные рассуждения [4, с. 9], остальные учащиеся не могут построить рассуждения при решении комбинаторных задач, найдя все возможные варианты без повторов. Причины этого были обнаружены в ходе психологического анализа практикуемых методов преподавания комбинаторики. Например, даже в наиболее удачных учебниках математики для средней и старшей школы объяснение комбинаторики часто начинается прямо с формулы. При этом предполагается, что действия по реальному построению наборов (комбинаций) элементов изучаемых соединений школьникам уже известны, а соотношение исходного множества с получаемыми на его основе наборами элементов носит очевидный характер.

Это означает, что, решая комбинаторные задачи, дети сами должны научиться выделять и соотносить между собой исходное множество и ряд свойств составляемых наборов. На практике большинство учеников с этим не справляется. Одним из способов повысить уровень усвоения комбинаторных знаний школьниками, по мнению детских психологов и педагогов, является визуализация изучаемого материала.

Проблемами визуализации при обучении математике занимался еще в 1957 г. Пьер Ван Хиель, впервые представивший модель обучения геометрии с опорой на развитие визуального мышления учащихся [5, с. 6].

Обычно выделяют следующие уровни взаимодействия визуального и других способов представления информации:

1. Динамическое визуальное представление, например наглядная генерация множества исходов в зависимости от случайно генерируемого количества объектов множества [6, c. 12].
2. Статическое визуальное представление, рисунок.
3. Абстрактное визуальное представление, граф.
4. Символическое/вербальное представление, определение/описание; название/ярлык; класс/род.

Концептуальное знание во многих случаях связано с визуальным представлением знаний, в то время как процедурное — с числовым, абстрактным и символическим представлением учебной информации. Для обучения математике важны оба типа знания: и концептуальное, и процедурное. Игнорирование одного из этих знаний (обычно это относится к первому типу) приводит к существенным пробелам в математической подготовке школьников, что и происходит зачастую при недостаточной обеспеченности графическим наглядным материалом.

Проблема соотношения визуального и других способов представления информации подробно рассмотрена В. А. Крутецким [7, с. 238] на примере аналитического, геометрического и гармонического типов склада математического ума школьников. Ученики с преобладающим аналитическим типом математического мышления имеют сильно развитые словесно-логические способности и не нуждаются в использовании наглядно-образных опор в процессе решения математических задач и доказательства теорем. Дети с геометрическим типом мышления имеют слабые словесно-логические, но очень сильно развитые наглядно-образные способности, что располагает их использовать визуальные опоры в решении задач. У учащихся гармонического типа, которых в экспериментах В. А. Крутецкого оказалось большинство, наблюдается равновесие в развитии словесно-логической и наглядно-образной составляющих математического мышления.

Фундаментальной работой по теме роли визуализации при обучении математике явилась книга «Визуализация в обучении математике», изданная в 1990 г. Математической ассоциацией Америки (МАА), в которой экспериментально доказано, что проблемы в обучении математике связаны с недостаточной визуальной поддержкой абстрактных научных понятий. Так, всего 50 обучающихся из 937 после прохождения курса математики могли вычислить простейшие интегралы.

Одной из причин такого низкого результата является оторванность аналитических процедур от визуальных.

Согласно опыту большинства школьных учителей самая большая проблема при решении комбинаторных задач заключается в формализации, переходе от вербальной формы к математической. В данном случае, это

1) опознание вида задачи (комбинаторная);

2) выбор комбинаторной схемы для решения;

3) применение формулы комбинаторики с конкретными числовыми данными.

Опознать комбинаторную задачу можно по трем признакам:

1. Все объекты задачи состоят из отдельных дискретных элементов;
2. Множества этих элементов конечны.
3. Используется два вида операций: отбор подмножеств и упорядочению элементов множества.

Комбинаторные задачи с точки зрения теории множеств — это задачи на определение числа возможных конечных множеств или кортежей с определенными свойствами, которые можно составить из данных элементов; или числа — соответствия, которые можно установить между элементами конечных множеств. К комбинаторным задачам теории вероятностей относят задачи, в которых подсчет какой-либо вероятности связан с комбинаторным подсчетом общего числа исходов и числа благоприятных исходов.

Способы решения комбинаторных задач обычно делят на две группы: «формальные» и «неформальные». При «формальном» пути решения нужно определить характер выборки, выбрать соответствующую формулу или комбинаторный принцип подставить числа и вычислить результат.

«Неформальный» способ решения на первый план выводит сам процесс составления различных комбинаторных конфигураций и часто связан с визуальными способами решения. И главная его задача быстро и правильно найти все возможные варианты.

К неформальным способам решения комбинаторных задач относят непосредственный перебор. Это самый элементарный способ, не требующий знания определений и формул. Поэтому именно его целесообразно использовать в основном общем образовании. При этом важен сам процесс перебора, так как, если действовать случайным, хаотичным образом, то не будет уверенности, что найдены все возможные комбинации. Чтобы избежать этого, нужно выполнять перебор по определенной системе.

Для этого используются такие способы визуализации решения задач как красочные рисунки, используемые при малом количестве объектов, и комбинаторные матрицы, таблицы, и графы, используемые при увеличении числа объектов. К сожалению, использование динамических визуальных представлений ограничивается техническими средствами, используемыми при обучении математики, но может с успехом использоваться, например при дистанционном обучении [8, с. 80] [9, с. 26].

Анализ особенностей комбинаторных задач и способов их решения позволяет сделать следующие выводы:

1. При составлении комбинаторных задач для учащихся начальных классов нужно использовать различные виды соединений, которые связаны размещениями, расстановками, сочетаниями.
2. Для решения комбинаторных задач в начальной школе должен использоваться неформальный метод, так как он учитывает особенности мышления этого возраста и не требует введения в программу дополнительных теоретических разделов.
3. Для решения комбинаторных задач младшим школьникам можно предложить способ перебора, составление таблиц и построение графов.
4. Для улучшения понимания комбинаторных знаний формальные методы решения должны быть заменены или дополнены визуальными.

Для упрощения формализации условия задачи и правильного выбора вида, а значит и формулы, комбинаторной задачи теории вероятностей ученикам можно предложить следующий вспомогательный графический материал (рис. 1), визуализирующий основную проблему при решении комбинаторных задач — выбор комбинаторной схемы:

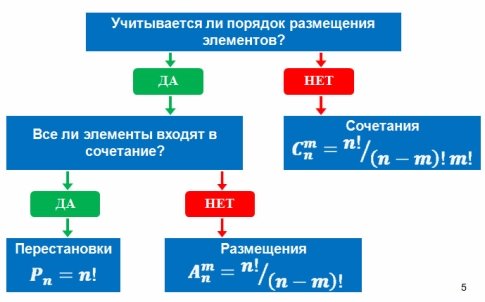
Рис. 1. Схема выбора комбинаторной формулы

Рассмотрим различные виды визуализации комбинаторных задач.

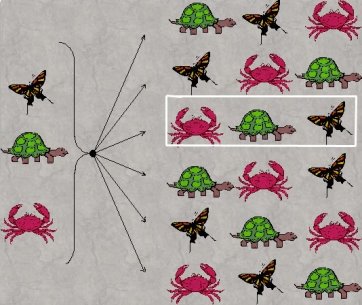
Рис. 2. Перестановки

Визуализация при малом числе объектов. На выставке представлены живые экспонаты: черепашка, краб и бабочка (рис. 2). Экскурсовод рассказывает о них в произвольном порядке. Какова вероятность того, что экскурсовод, начав с краба последней расскажет о бабочке?

Из рисунка следует, что сделать это можно единственно возможным способом из шести способов порядка знакомства с экспонатами, искомая вероятность равна 1/6.

Визуализация спомощью графов. Какова вероятность того, что четное двузначное число, составленное из цифр 0, 2, 3, 6, 7, 9, будет больше 50 (рис. 3)?

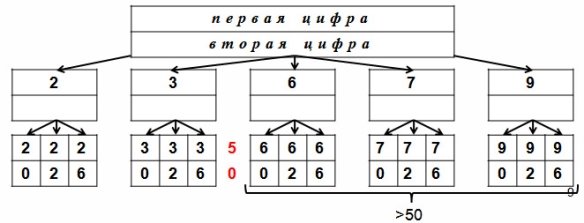
Рис. 3. Дерево возможностей

Из рисунка видно, что условию задачи удовлетворяют 9 исходов из 15 возможных, то есть искомая вероятность равна 0.6

Визуализация спомощью таблиц. В 10 классе 6 человек (Галя, Света, Катя, Оля, Максим, Витя) учатся на все пятерки. Президентскую стипендию назначили только четырем учащимся. Какова вероятность того, что стипендию будут получать только девочки?

Обозначим первыми заглавными буквами имен учащихся. Возможны следующие тройки (таблица 1):

Таблица 1

Варианты выбора 4 имен из 6

Г-С-К-О	Г-С-К-М	Г-С-К-В
Г-С-О-М	Г-С-О-В	Г-С-М-В
С-К-О-М	С-К-О-В	С-К-М-В
К-О-М-В	С-О-М-В	Г-К-О-В
Г-К-О-В	Г-О-М-В	Г-К-М-В

Таким образом, 4 учеников можно выбрать 15-ю способами, вероятность того, что это будут только девочки, равна 1/15.

Визуализация спомощью матрицы. Игральную кость бросают 2 раза. Какова вероятность, что сумма выпавших очков будет не менее 7 (рис. 4)?

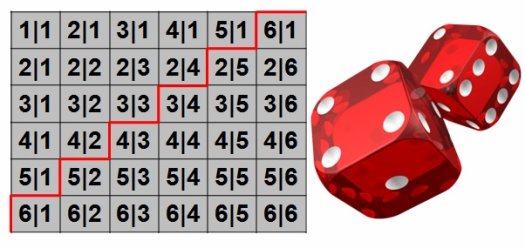
Рис. 4. Результаты двукратного бросания кости

Из таблицы полных исходов видно, что условию задачи удовлетворяет 21 исход из 36 возможных, то есть искомая вероятность равна 21/36.

Литература:

1. Бурменская Г. В., Евдокимова Л. В. Формирование комбинаторного мышления у младших школьников и подростков/ Вопросы психологии, 2007 [электронный ресурс]. Режим доступа: http://www.vash-psiholog.info/voprospsih/214/17759-formirovanie-kombinatornogo-myshleniya-u-mladshix-shkolnikov-i-podrostkov.html
2. Виноградова Е. П. Опыт включения комбинаторных задач в школьный курс математики [электронный ресурс]. Режим доступа: http://superinf.ru/view_helpstud.php?id=1987
3. Пиаже Ж., Инельдер Б. Генезис элементарных логических структур. Классификации и сериации / пер. с фр. Э. М. Пчелкина; послесл. А. Н. Леонтьева и О. К. Тихомирова. — М.: Изд-во иностр. лит., 1963. — 448 с.
4. Белокурова Е. Е. Методика обучения младших школьников проведению комбинаторных рассуждений при решении задач, Санкт-Петербург, 1993, 23с.
5. Пресмег Н., Чошанов М. От кубиков до матанализа. Роль визуализации в процессе обучения математике// Учительская газета, М., N010. С. 5–7.
6. Драгныш Н. В. Построение генератора случайных чисел на основе параллельного перемешивания. Наука, техника и образование. 2015. № 6 (12). С. 12–14.
7. Крутецкий В. А. Психология математических способностей школьников. М.: Институт практической психологии; Воронеж: НПО МОДЕК, 1998. (серия «Психологи отечества») — 416 с.
8. Драгныш Н. В. Использование инновационных технологий для преподавания курса «Теория вероятностей и математическая статистика». Дискуссия. 2010. № 8. С. 80–83.
9. Драгныш Н. В. Использование методов имитационного моделирования для преподавания курса «Теория вероятностей и математическая статистика». Актуальные проблемы гуманитарных и естественных наук. 2011. № 12. С. 26–29.