В последнее время нечеткое моделирование является одной из наиболее активных и перспективных направлений прикладных исследований в области управления и принятии решений.
В области управления техническими системами нечеткое моделирование позволяет получать более адекватные результаты по сравнению с результатами, которые основываются на использовании традиционных аналитических моделей и алгоритмов управления. Диапазон применения нечетких методов расширяется с каждым годом [2].
Аппроксимация является неотъемлемой частью процесса моделирования, который, как правило, предшествует процессу создания системы управления. Значимость моделирования, скорее всего, даже выше, чем значимость собственно управления, поскольку область применения моделирования несравненно шире как общего средства и метода для решения проблем практически во всех областях.
Основную задачу теории аппроксимации можно сформулировать следующим образом: на некотором точечном множестве в пространстве произвольного числа измерений заданы 2 функции 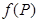 и
и 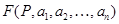 от точки
от точки 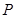 , из которых вторая зависит ещё от некоторого числа параметров
, из которых вторая зависит ещё от некоторого числа параметров 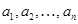 . Эти параметры требуется определить так, чтобы уклонение функции
. Эти параметры требуется определить так, чтобы уклонение функции 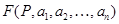 от функции
от функции 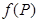 было наименьшим. При этом должно быть указано, что понимают под уклонением (расстоянием)
было наименьшим. При этом должно быть указано, что понимают под уклонением (расстоянием) 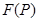 от
от 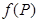 .
.
В данной статье рассматриваются недостатки сложившегося в области нечеткого моделирования подхода, называемого в данной статье «традиционным», предлагается методика определения функций вида функций принадлежности.
1 Анализ «традиционного» подхода
Сформулируем задачу аппроксимации системой нечеткого вывода («традиционный» подход). На некотором точечном множестве в пространстве произвольного числа измерений задана функция 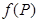 . А также имеется система нечеткого вывода, число входных переменных которой равно размерности пространства, в котором задана
. А также имеется система нечеткого вывода, число входных переменных которой равно размерности пространства, в котором задана 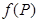 , число выходных переменных равно количеству выходных переменных функции
, число выходных переменных равно количеству выходных переменных функции 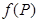 . База правил содержит в себе соотношения между входными и выходными переменными. Для каждой переменной определен вид функций принадлежности (треугольный, кривой Гаусса или любой другой), а также заданы начальные параметры функций принадлежности. Предполагается, что в пределах каждой переменной выбран единообразный вид функции принадлежности термов, кроме, быть может, крайних. Совокупность параметров всех функций принадлежности составляет множество параметров системы
. База правил содержит в себе соотношения между входными и выходными переменными. Для каждой переменной определен вид функций принадлежности (треугольный, кривой Гаусса или любой другой), а также заданы начальные параметры функций принадлежности. Предполагается, что в пределах каждой переменной выбран единообразный вид функции принадлежности термов, кроме, быть может, крайних. Совокупность параметров всех функций принадлежности составляет множество параметров системы 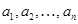 . Во множество параметров системы может также входить количество функций принадлежности в каждой переменной. Эти параметры требуется определить таким образом, чтобы уклонение статической характеристики системы нечеткого вывода от функции
. Во множество параметров системы может также входить количество функций принадлежности в каждой переменной. Эти параметры требуется определить таким образом, чтобы уклонение статической характеристики системы нечеткого вывода от функции 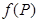 было наименьшим.
было наименьшим.
Слабой стороной этого подхода является ограниченная точность при заданном количестве функций принадлежности, и, как следствие, необходимость увеличивать это количество для повышения точности.
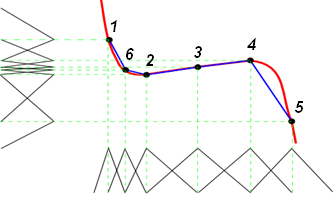
Рис. 1. Нечеткая система интерполирует расстояние между заданными значениями (в данном случае отрезками прямых)
На Рис. 1 показана нечетная функция. Точки 1, 2, 3, 4, 5 взяты с равным интервалом по оси абсцисс. Вершины термов соответствуют значениям функции в точках. В данном примере интервалы между точками интерполируются системой нечеткого вывода отрезками прямых. Однако в зависимости от выбора формы функций принадлежности, а также методов агрегирования и дефазификации вид отрезков, аппроксимирующих кривую может изменяться.
Как видно из рисунка, аппроксимирующая кривая на отрезке 4–5 существенно уклоняется от заданной функции. Для увеличения точности аппроксимации на симметричном интервале 1–2 взята дополнительная точка 6. Она взята таким образом, что ее проекция на ось абсцисс находится ровно посередине между проекциями точек 1 и 2 на ту же ось. Для ее описания также вводится по одному дополнительному терму во входную и выходную переменные, а параметры соседних термов несколько изменяются. Так продолжается до тех пор, пока необходимая точность не будет достигнута.
Кроме того, при использовании такого подхода в алгоритме нечеткого вывода Мамдани с фазификацией по методу центра тяжести или центра площади возникают трудно предсказуемые отклонения от аппроксимируемой функции.
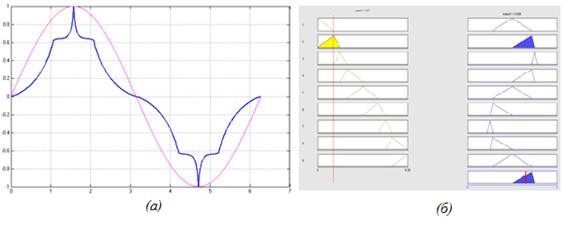
Рис. 2. Центр тяжести не совпадает с вершиной терма выходной переменной (б), вызывая непредвиденные отклонения (а)
Рассмотрим это явление на примере аппроксимации функции 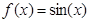 . Если с целью увеличения точности аппроксимации без увеличения количества функций принадлежности сдвинуть вершины некоторых функции принадлежности ближе к наиболее искривленным участкам функции (к «горбам»), то результат, окажется обратным ожидаемому (см. Рис. 2-а). Это связано с тем, что центр тяжести или площади (в зависимости от используемого метода) не совпадает с вершиной функции принадлежности (Рис. 2-б). Это явление оказывает влияние и на соседние области, поскольку в выводе обычно участвуют и соседние правила.
. Если с целью увеличения точности аппроксимации без увеличения количества функций принадлежности сдвинуть вершины некоторых функции принадлежности ближе к наиболее искривленным участкам функции (к «горбам»), то результат, окажется обратным ожидаемому (см. Рис. 2-а). Это связано с тем, что центр тяжести или площади (в зависимости от используемого метода) не совпадает с вершиной функции принадлежности (Рис. 2-б). Это явление оказывает влияние и на соседние области, поскольку в выводе обычно участвуют и соседние правила.
2 Методика определения вида функций выходной переменной
Поскольку формальное определение нечеткого множества не накладывает никаких ограничений на выбор конкретной функции принадлежности для его представления, задачу аппроксимации можно сформулировать следующим образом. На некотором точечном множестве в пространстве произвольного числа измерений задана функция 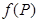 . А также имеется система нечеткого вывода, число входных переменных которой равно размерности пространства, в котором задана
. А также имеется система нечеткого вывода, число входных переменных которой равно размерности пространства, в котором задана 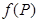 , число выходных переменных равно количеству выходных переменных функции
, число выходных переменных равно количеству выходных переменных функции 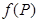 . База правил содержит в себе соотношения между входными и выходными переменными. Требуется определить форму, а также, возможно, количество, функций принадлежности таким образом, чтобы уклонение статической характеристики системы нечеткого вывода от функции
. База правил содержит в себе соотношения между входными и выходными переменными. Требуется определить форму, а также, возможно, количество, функций принадлежности таким образом, чтобы уклонение статической характеристики системы нечеткого вывода от функции 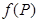 было наименьшим.
было наименьшим.
В результате исследований была разработана следующая методика. Наиболее подходящим алгоритмом нечеткого вывода оказался алгоритм Цукамото.
На первом этапе аппроксимируемая функция разбивается на участки монотонности. При наличии интервалов, на которых функция симметрична, этот интервал берется целиком без разбивания на участки монотонности.
На втором этапе термы входной переменной задаются таким образом, что на каждом участке монотонности ненулевой степенью истинности обладают только два правила. Функции принадлежности имеют треугольную форму. Для интервалов, на которых функция симметрична, задается один терм треугольной формы, основания треугольника находятся на границе интервала, вершина — в центре (Рис. 9).
На третьем этапе определяются функции принадлежности выходной переменной. Первая функция принадлежности определяется следующим образом. При одном и том же значении 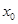 определяется степень истинности входной переменной и значение аппроксимируемой функции. По полученным значениям строится точечная зависимость
определяется степень истинности входной переменной и значение аппроксимируемой функции. По полученным значениям строится точечная зависимость 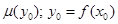 , которая дает представление о форме выходной переменной.
, которая дает представление о форме выходной переменной.
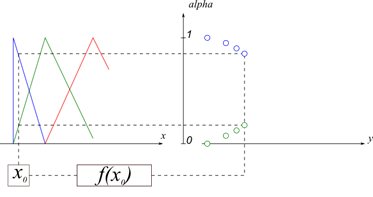
Рис. 3. Построение точечной зависимости
Вторая и последующие определятся по тому же принципу с условием того что значение на выходе системы есть сумма значений выходных термов, умноженных на соответствующие уровни отсечения (Рис. 4), то есть по формуле:
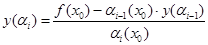
где 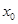 — точка, для которой происходит поиск вида функции принадлежности;
— точка, для которой происходит поиск вида функции принадлежности;
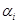 — степень истинности (уровень отсечения) i-го правила для
— степень истинности (уровень отсечения) i-го правила для 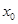 ;
;
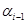 — степень истинности (уровень отсечения) (i-1)-го правила для
— степень истинности (уровень отсечения) (i-1)-го правила для 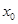 ;
;
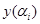 — значение терма i-го при уровне отсечения
— значение терма i-го при уровне отсечения 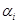 ;
;
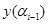 — значение терма (i-1)-го при уровне отсечения
— значение терма (i-1)-го при уровне отсечения 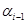 ;
;
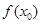 — значение аппроксимируемой функции при
— значение аппроксимируемой функции при 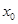 .
.
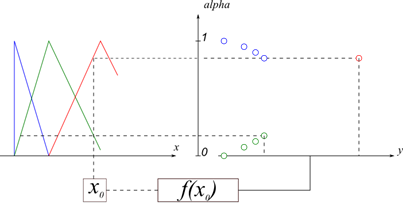
Рис. 4. Каждая последующая функция принадлежности строится с учетом значений предыдущей
На четвертом этапе подбирается функция принадлежности наиболее точно описывающая полученное множество. При использовании элементарных функций необходимо поступить следующим образом.
Пусть по точечному виду выбрана некая элементарная функция 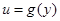 , аппроксимирующая данную зависимость. Необходимо ввести в эту функцию коэффициенты
, аппроксимирующая данную зависимость. Необходимо ввести в эту функцию коэффициенты 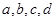 следующим образом
следующим образом 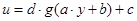 . В таком случае коэффициенты
. В таком случае коэффициенты 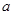 и
и 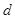 будут отвечать за сжатие/растяжение по оси абсцисс и ординат соответственно, а коэффициенты
будут отвечать за сжатие/растяжение по оси абсцисс и ординат соответственно, а коэффициенты 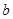 и
и 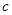 — за смещение по осям абсцисс и ординат.
— за смещение по осям абсцисс и ординат.
Далее с использованием методов оптимизации или при помощи эксперта происходит подбор коэффициентов.
На пятом этапе происходит формирование базы правил. Устанавливается соответствие между термами входной и выходной переменных, вес импликационных правил принимается равным единице:
If (input1 is mf1) then (output1 is mf1) (1)
If (input1 is mf2) then (output1 is mf2) (1)
If (input1 is mf3) then (output1 is mf3) (1)
и так далее …
В Таблице 1 приведены данные по среднеквадратичному отклонению кривых, полученных при использовании различных вариантов нечеткого моделирования, от аппроксимируемой функции y = sin(x). Под словом «равномерный» подразумевается, что функции принадлежности входной переменной равномерно распределены на всем интервале. Под словом «смещенный» подразумевается, что вершины некоторых термов были смещены к наиболее характерным изгибам («горбам») функции.
Таблица 1
Результаты аппроксимации различными нечеткими системами
|
Алгоритм |
Кол-во функций принадлежности |
Кол-во правил |
Ср. кв. отклонение | ||
|
на входе |
на выходе |
общее | |||
|
Мамдани |
5 |
3 |
8 |
5 |
0,8602 |
|
Мамдани, равномерный |
9 |
5 |
14 |
9 |
1,0490 |
|
Мамдани, смещенный |
9 |
5 |
14 |
9 |
1,7950 |
|
Сугено, равномерный |
9 |
5 |
14 |
9 |
0,2079 |
|
Сугено, смещенный |
9 |
5 |
14 |
9 |
0,2443 |
|
Цукамото, предлагаемый |
2 |
2 |
4 |
2 |
0,0317 |
Заключение
В результате работы были рассмотрены существующие подходы к аппроксимации нечеткими системами. В них, несмотря на то, что формальное определение нечеткого множества не накладывает никаких ограничений на его форму, используются лишь некоторые виды функций принадлежности. А для увеличения точности аппроксимации приходится увеличивать их количество.
Целью исследования было проверить эффективность такого подхода. В результате был предложен альтернативный подход, в котором сначала определяется вид нечеткого множества аппроксимирующей системы, а затем подбирается функция принадлежности, способная описать это множество. А также была разработана методика синтеза таких систем.
Далее был произведен сравнительный анализ предложенной методики с существующими подходами. Аппроксимация по предложенной методике подтвердила ее высокую эффективность в сравнении с традиционно применяемым методом. При существенно меньшем количестве функций принадлежности и правил в базе знаний, предложенная система на порядок превосходит описанные по точности аппроксимации. Полученные результаты свидетельствуют о перспективности такого подхода.
Следует отметить, что точность аппроксимации системой в целом напрямую зависит от точности аппроксимации отдельных множеств выходных переменных. В работе для этих целей были использованы элементарные функции (такие как прямая, гипербола, показательная функция), которые не превосходят по сложности функции, традиционно используемые для описания нечетких множеств (такие как функция Гаусса, треугольная или трапецеидальная функции, и др.). Учитывая также, что общее количество функций принадлежности предлагаемой системе меньше, можно говорить о ее более высокой вычислительной эффективности.
В настоящее время продолжаются работы в данном направлении с целью выяснения возможности применения подобного подхода для аппроксимации более сложных зависимостей, что в конечном итоге должно помочь в создании идентифицирующего устройства на основе нечеткой логики.
Литература:
1. Леоненков, А. В. Нечеткое моделирование в среде MATLAB и fuzzyTECH / А. В. Леоненков. — СПб.: БХВ-Петербург, 2005. — 736 с.
2. Прикладные нечеткие системы: Пер. с япон. / К. Асаи, Д. Ватада, С. Иваи и др.; под редакцией Т. Тэрано, К. Асаи, М. Сугэно. — М.: Мир, 1933. — 368 с.
3. Горбань, А. Н. Обобщенная аппроксимационная теорема и вычислительные возможности нейронных сетей / А. Н. Горбань // Сибирский журнал вычислительной математики. — 1998. — № 1. — С. 12–24.
4. Kosko, B. Fuzzy systems as universal approximators / B. Kosko // IEEE Intrnational Conference. — 1992. — C. 1153–1162.
5. Wang, L.-X. Fuzzy systems are universal approximators/ L.-X. Wang// IEEE Intrnational Conference. — 1992. — C. 1163–1170.
6. Castro, J. L. Fuzzy logic controllers are universal approximators/ J. L. Castro, Systems, Man and Cybernetics. — 1995. — C. 629–635

