Предположим, что во множестве действительных чисел функция ![]() имеет локально суммируемые производные порядка
имеет локально суммируемые производные порядка ![]() , а также для интервала
, а также для интервала ![]() интеграл
интеграл ![]() ограничен. Положим, что функция
ограничен. Положим, что функция ![]() является периодической.
является периодической.
В пространстве ![]() рассмотрим интерполяционную формулу вида
рассмотрим интерполяционную формулу вида
![]() .(1)
.(1)
Здесь ![]() и параметры
и параметры ![]() соответственно называются узлами и коэффициентами интерполяционной формулы (1).
соответственно называются узлами и коэффициентами интерполяционной формулы (1).
Разность ![]() называется погрешностью интерполяционной формулы (1). Значение этой погрешности в некоторой точке
называется погрешностью интерполяционной формулы (1). Значение этой погрешности в некоторой точке ![]() является линейным функционалом на функциях
является линейным функционалом на функциях ![]() , т. е.
, т. е.
![]()
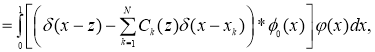 (2)
(2)
где ![]() — дельта-функция Дирака,
— дельта-функция Дирака, ![]() ; здесь
; здесь ![]() принимает все целые значения и
принимает все целые значения и
![]() (3)
(3)
является функционалом погрешности интерполяционной формулы (1) и принадлежит пространству ![]() .
.
Пространство ![]() состоит из всех периодических функционалов (3), которые ортогональны к единице. На основании неравенства Коши-Шварца погрешность (2) формулы (1) оценивается с помощью нормы функционала погрешности (3). Следовательно, оценка погрешности интерполяционной формулы (1) на функциях пространства
состоит из всех периодических функционалов (3), которые ортогональны к единице. На основании неравенства Коши-Шварца погрешность (2) формулы (1) оценивается с помощью нормы функционала погрешности (3). Следовательно, оценка погрешности интерполяционной формулы (1) на функциях пространства ![]() приводится к нахождению нормы функционала погрешности
приводится к нахождению нормы функционала погрешности ![]() в сопряженном пространстве
в сопряженном пространстве ![]() .
.
Таким образом, отсюда мы получаем первую задачу.
Задача 1. Найти норму функционала погрешности ![]() интерполяционной формулы (1) в пространстве
интерполяционной формулы (1) в пространстве ![]() .
.
В этой задаче для экстремальной функции имеет место следующая
Теорема 1. Явное выражение для экстремальной функции ![]() функционала погрешности (3) определяется формулой
функционала погрешности (3) определяется формулой
![]() (4)
(4)
где 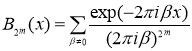 является полиномом Бернулли,
является полиномом Бернулли, ![]() – константа.
– константа.
Доказательство. Используем формулы преобразования Фурье, данный в [17]
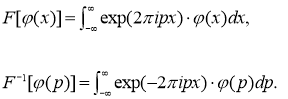
Свертка двух функций определяется формулой
![]()
Применяя к обеим частям равенства (4) преобразование Фурье и используя известные формулы (см. [17])
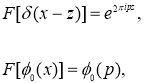
получаем
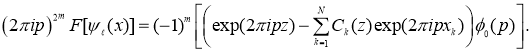 (5)
(5)
Равенства (5) равна нулю в начале координат. Следовательно, обе части уравнения (5) делятся на ![]() .
.
Функция ![]() определяется из (5) до выражения
определяется из (5) до выражения
![]()
Таким образом, из (5) имеем
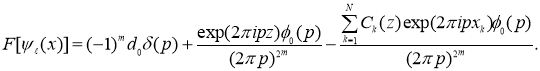
Отсюда, с учетом
![]() и
и ![]()
получаем
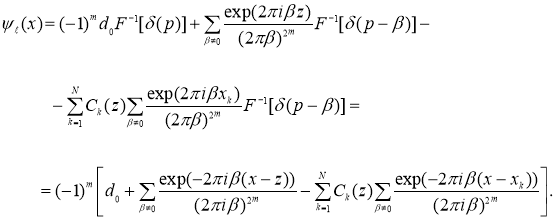 Отсюда, используя определение полинома Бернулли
Отсюда, используя определение полинома Бернулли ![]() , получим (4).
, получим (4).
Теорема 1 доказана.
Литература:
- Соболев С. Л. Введение в теорию кубатурных формул. -М.: Наука, 1974. -808 с.
- Соболев С. Л., Васкевич В. Л. Кубатурные формулы. — Новосибирск: Изд-во ИМ СО РАН, 1996. — 484 с.

