Данная работа посвящена поиску решения нелинейного интегрально — дифференциального уравнения, лежащего в основе математической модели, описывающей эволюцию вида во времени на основе наследования непрерывно — распределенных признаков, придуманная А. В. Нориным и М. Кузнецовым в 2012г. [1].
Интересующее нас интегро-дифференциальное уравнение [2] выглядит следующим образом и является нелинейным:
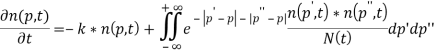
Разложим функции входящие в данное уравнение по ![]() , т. е. запишем формальный ряд. Затем, подставив в исходное уравнение, приравняем коэффициенты при одинаковых степенях
, т. е. запишем формальный ряд. Затем, подставив в исходное уравнение, приравняем коэффициенты при одинаковых степенях ![]() . Получаем цепочку уравнений, где в каждом следующем неизвестным является только одна функция, если предыдущие уравнения решены. Исходя из вышесказанного, можно сделать вывод, что, решив первое уравнение, мы получим решения и последующих.
. Получаем цепочку уравнений, где в каждом следующем неизвестным является только одна функция, если предыдущие уравнения решены. Исходя из вышесказанного, можно сделать вывод, что, решив первое уравнение, мы получим решения и последующих.
Рассмотрим уравнение, получившееся приравниванием коэффициентов при ![]() :
:
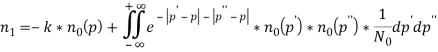
Запишем в более удобной форме:
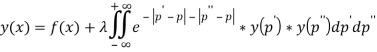
В таком виде это уравнение является нелинейным интегральным уравнением Фредгольма 2 рода. Как и многие другие виды [3] нелинейных интегральных уравнений, оно является нерешенным.
Разделим ядро на две функции от двух переменных:
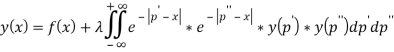
Или:
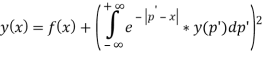
В теории линейных интегральных уравнений существует множество методов их решений, попробовав применить большую часть к нашему получившемуся нелинейному (из-за квадрата) интегральному уравнению, успешным окажется только один. Это метод разложения по ![]() Известный также, как метод последовательных приближений. Построим схожий алгоритм для решения нелинейного интегрального уравнения.
Известный также, как метод последовательных приближений. Построим схожий алгоритм для решения нелинейного интегрального уравнения.
Запишем формальный ряд разложения по ![]()
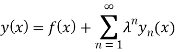
Подставим это разложение в наше уравнение и приравняем коэффициенты при одинаковых степенях ![]()
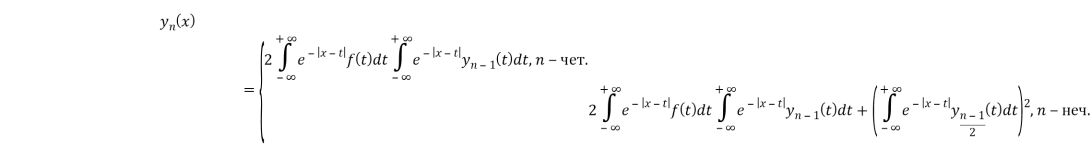
Покажем сходимость данного разложения. Если приближения не возрастают, т. е.
![]()
то ряд будет сходиться при любых ![]() . Пусть выполняется следующее условие:
. Пусть выполняется следующее условие:
![]()
Тогда членом
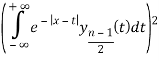
можно пренебречь. Следовательно, получим общую формулу приближений для четных и нечетных ![]() :
:
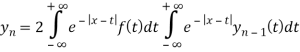
Перейдем к операторной записи интеграла:
![]()
Оценим ![]()
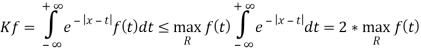
Т. к.
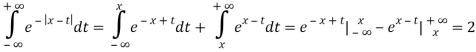
Попробуем оценить ![]() :
:
![]()
![]()
Из этой оценки следует, что ряд
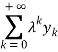
Мажорируется числовым рядом
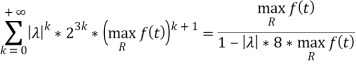
Сходящимся в круге
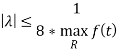
Итак, получили алгоритм решения нелинейного интегрального уравнения при заданном свободном члене и показали ограничение на ![]() , которое должно выполняться, чтобы метод работал.
, которое должно выполняться, чтобы метод работал.
Литература:
- А. В. Норин, М. В. Кузнецов. «Уравнения математической генетики типа Костицына с непрерывно-распределенными признаками» в сб. «Альманах», СПб, 2012.
- https://ru.wikipedia.org/wiki/Интегральное_уравнение
- П. П. Забрейко, А. И. Кошелев, М. А. Красносельский. «Интегральные уравнения», Москва, 1968.

