Исследования разностных схем проводятся, разбивая на два этапа.
I этап. Проверка аппроксимации. I этап состоит в проверке того, что интересующее нас решение 
дифференциального уравнения
,
после замены его на следующее разностное уравнение
удовлетворяет ли его, т. е. выполняются ли следующие равенства:
(здесь 
шаги разностной схемы). Проверка этих неравенств называется проверкой аппроксимации.
II этап. Проверка устойчивости.
Проверка следующего неравенства
для решений разностного уравнения, называется проверкой устойчивости разностной схемы.
Теперь в области 
рассмотрим следующее уравнения:
(1)
Мы через 
обозначим линейный, дифференциальный оператор с частными производными второго порядка:
.
Здесь 
, 
, 
, 
, 
— заданные функции, которые удовлетворяют следующие условиям:
1) 
и 
.
2) 
и 
.
3)
.
4) 
.
— пространство непрерывных функций, 
— замыкание 
. Область 
разделим на три области:
Здесь 
,
,
- граница области 
.
— внутренняя нормаль проведений к границе 
.
Определим, к какому типу принадлежит (1) уравнение в области . Введем следующие обозначения: 
.
Мы знаем в области 
значения выражения 
может быть отрицательным, положительным или равным нулю, тогда соответственно в (1) уравнение называется или эллиптического, или гиперболического или параболического типа.
Здесь 
, 
.
По классификацию уравнений частного производного второго порядка (1) уравнения принадлежит к уравнениям смешанного типа в области
.
Для уравнения (1) изучаем следующую краевую задачу:
Краевая задача: Найти функцию 
, удовлетворяющую в области уравнения (1), а при 
граничное условие:
(2)
пространство функций, принадлежащих классу 
и удовлетворяющих условию (2).
Для решения краевой задачи (1) — (2), мы используем приближенной (численный) метод (метод разностных схем).
В области 
построим разностную сетку шагами 
, (
, 
).
Приближенное решение (1)-(2) краевой задачи в точке 
обозначим через 
.
Здесь, — узловые точки, получение пересечением прямых линий 
. Введем следующие операторы сдвига 
и разностные 
операторы:
, 
,
.
Тогда аппроксимируем краевую задачу (1)-(2), следующей схемой [2]:
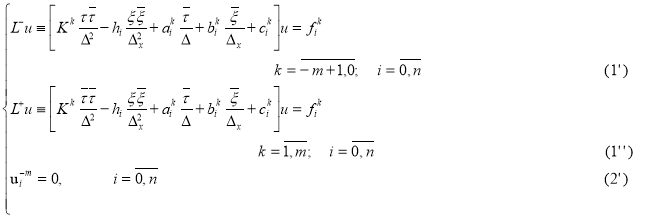
Это схема имеет первую аппроксимацию по 
.
Литература:
- Алоев Р. Д., Рахмонов Х. О., Шарипова Ш. Исследование разностной модели краевой задачи для уравнения смешанного типа. «Оптимизация численных методов» Тезисы докладов международной научной конференции «Оптимизация численных методов», посвященной 90-летию со дня рождения С. Л. Соболев. Уфа ИМВЦ УНЦ РАН 1998г, 4–5-с.
- Меражова Ш. Численное решения первой и второй краевой задачи для уравнения смешанно-составного типа. В. И. Романовский юбилейига бағишланган конференция материаллари тўплами. Тошкент, 2004, 81–84-с.
