В настоящей работе рассматривается наиболее распространенный вид кубатурной формулы [1]
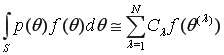 (1)
(1)
в пространстве ![]() на поверхности сферы, где
на поверхности сферы, где ![]() мерная единичная сфера,
мерная единичная сфера, ![]() — интегрируемая функция по сфере
— интегрируемая функция по сфере ![]() , т. е.
, т. е. ![]()
и 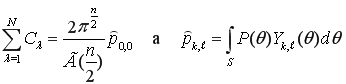 ,
,
где ![]() — сферическая гармоника порядка
— сферическая гармоника порядка ![]() вида
вида ![]() . Здесь индекс
. Здесь индекс ![]() получен в результате нумерации сферических функций одного и того же порядка
получен в результате нумерации сферических функций одного и того же порядка ![]() и меняется в пределах
и меняется в пределах ![]()
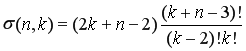 — число линейно независимых сферических гармоник порядка
— число линейно независимых сферических гармоник порядка ![]() . Функции
. Функции![]() будем считать ортогональными на сфере
будем считать ортогональными на сфере ![]() .
.
Функционал погрешности кубатурной формулы (1) имеет следующий вид:
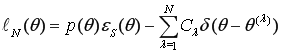 , (2)
, (2)
где ![]() — дельта — функция Дирака,
— дельта — функция Дирака, ![]() и
и ![]() — коэффициенты и узлы кубатурной формулы (1).
— коэффициенты и узлы кубатурной формулы (1).
Следующая теорема без доказательства приведена в работе Г. Н. Салихова [2].
Теорема 1. Норма функционала погрешности ![]() кубатурной формулы (1) над пространством
кубатурной формулы (1) над пространством ![]() равна
равна
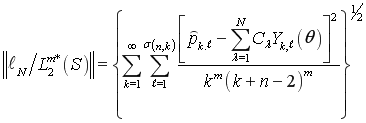 ,
,
где
![]() .
.
Доказательство. Известно [2], что если ![]() , то для абсолютной и равномерной сходимости ряда
, то для абсолютной и равномерной сходимости ряда
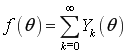 ,
,
где ![]() — сферические гармоники порядка
— сферические гармоники порядка ![]() , достаточно выполнение условия
, достаточно выполнение условия ![]() .
.
Таким образом, функция ![]() может быть разложена в равномерно и абсолютно сходящийся ряд по сферическим гармоникам
может быть разложена в равномерно и абсолютно сходящийся ряд по сферическим гармоникам
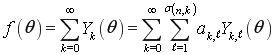 , (3)
, (3)
где ![]() — сферические гармоники порядка
— сферические гармоники порядка ![]() вида
вида ![]() ;
;
![]() ;
; ![]() — число линейно независимых сферических гармоник:
— число линейно независимых сферических гармоник:
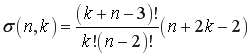 .
.
Подставляя (3) в левую часть (1), находим
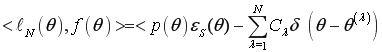 ,
,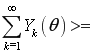
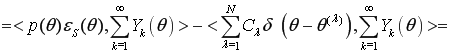
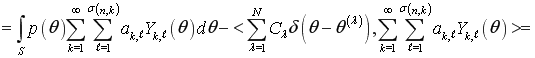
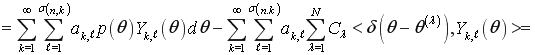
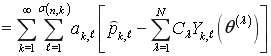 . (4)
. (4)
Если в правой части (4) ![]() умножить на
умножить на ![]() , а кубатурную сумму разделить на этот множитель и применить неравенство Коши, то получим
, а кубатурную сумму разделить на этот множитель и применить неравенство Коши, то получим
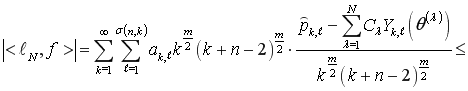
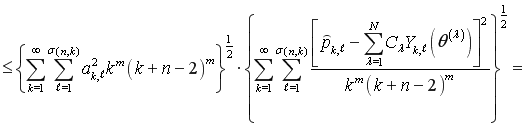
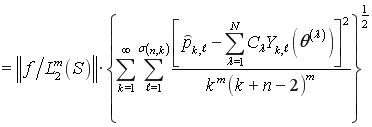 . (5)
. (5)
Из (5) следует
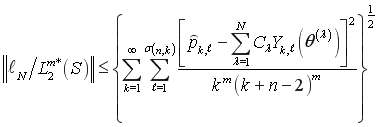 . (6)
. (6)
Для того чтобы получить равенство (6) рассмотрим функцию
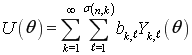 , (7)
, (7)
где
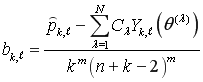 . (8)
. (8)
Так как для сферических функций имеет место оценка
max ![]() ,
,
то из определения (8) коэффициентов ряда (7) следует, что
![]() .
.
Вычислив погрешность кубатурной формулы (3) для этой функции, получим следующее равенство:
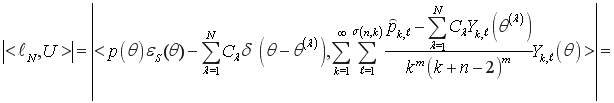
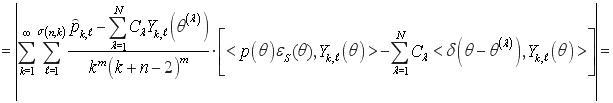
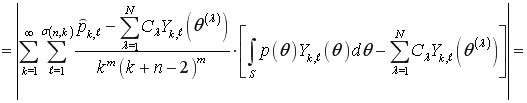
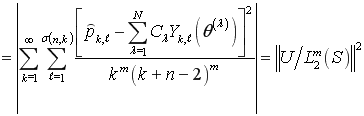 . (9)
. (9)
Сопоставляя (6) и (9) находим, что
![]() ,
,
где ![]() является экстремальной функцией для кубатурной формулы (1), т. е.
является экстремальной функцией для кубатурной формулы (1), т. е. ![]() — функция Рисса для функционала погрешности
— функция Рисса для функционала погрешности ![]() , что и требовалось доказать.
, что и требовалось доказать.
Теорема 2. Равенство (9) подтверждает, что
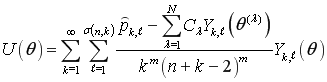 ,
,
действительно, является экстремальной функцией для кубатурной формулы (1) и ![]() , где
, где ![]() - ортонормированная сферическая гармоника порядка
- ортонормированная сферическая гармоника порядка ![]() , вида
, вида ![]() и
и ![]() - число линейно независимых сферических гармоник порядка
- число линейно независимых сферических гармоник порядка ![]() .
.
Литература:
- Соболев С. Л. Введение в теорию кубатурных формул. — М.: Наука, 1974. — 808 с.
- Салихов Г. Н. Кубатурные формулы для многомерных сфер. — Ташкент: Фан, 1985.
- Рамазанов М. Д. Лекции по теории приближенного интегрирования. Уфа, 1973. — 173с.

