В одномерной ограниченной области исследована вторая начально-краевая задача для однородного псевдопараболического уравнения с дробной по времени производной Капуто. Установлены условия однозначной разрешимости рассматриваемой задачи в классе непрерывно дифференцируемых функций. Существование решения первой краевой задачи доказано методом Фурье.

Ключевые слова: псевдопараболическое уравнение, краевые задачи, дифференциальное уравнение дробного порядка, дробная производная Капуто, дробный интеграл Римана-Лиувилля, метод Фурье, функция Миттаг-Леффлера.

In a one-dimensional bounded domain, the second initial-boundary value problem for a homogeneous pseudoparabolic equation with a time-fractional Caputo derivative is studied. Conditions for the unique solvability of the problem under consideration in the class of continuously differentiable functions are established. The existence of a solution to the first boundary value problem is proved by the Fourier method.

Keywords: pseudoparabolic equation, boundary value problems, fractional order differential equation, Caputo fractional derivative, Riemann-Liouville fractional integral, Fourier method, Mittag-Leffler function,

Введение

Дифференциальные уравнения с дробными производными естественным образом возникают в ряде областей науки, таких как физика, инженерия, биофизика, явления кровотока, аэродинамика, электронно-аналитическая химия, биология, теория управления и т. д. Более подробную информацию о таких уравнений можно найти в работах [1–4].

Псевдопараболические уравнения с дробными производными возникают при описании процессов фильтрации жидкости в сильно пористой (фрактальной) среде, фильтрации жидкости в трещиноватой среде с фрактальной геометрией трещин, переноса почвенной влаги в зоне с учетом ее движения против потенциала влажности [4–7]. В связи с этим возникает необходимость исследования краевых задач для дифференциальных уравнений с дробными производными и разработки методов их решений.

Задача Коши, начально-краевые задачи для псевдопараболического уравнения, в том числе для уравнения Аллера с дробными производными Римана-Лиувилля были изучены в работах [8–11].

В данной работе изучается первая начально-краевая задача для одномерного псевдопараболического уравнения уравнения с дробными производными Капуто.

1. Определение дробных проиводных и интегралов.

Введем некоторые понятия, необходимые для дальнейшего исследования.

Определение 1. Дробным дифференциальным оператором Капуто порядка для дифференцируемой функции называется оператор, определенный выражением [3,4]:

(1.1)

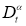
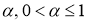
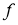
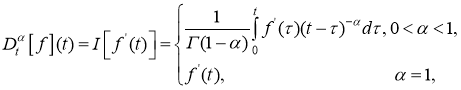
где гамма функция.

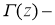
Определение 2. Дробным интегральным оператором Римана-Лиувилля порядка для интегрируемой функции называется оператор, определенный выражением [3,4]:

(1.2)

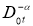
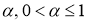
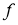
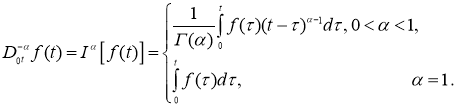
Определение 3. Двупараметрическая функция определяемая формулой [3]:

, (1.3)

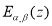
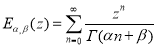
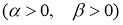
называется функцией Миттаг-Леффлера.

Приведем некоторые соотношения, приведенные в [3]:

(1.4)

(1.5)

(1.6)

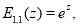
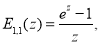
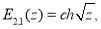
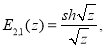
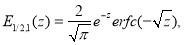
При получим однопараметрическую функцию Миттаг-Леффлера:

.(1.7)

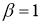
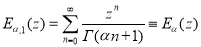
Обобщение формулы Ньютона-Лейбница, при

(1.8)

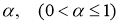
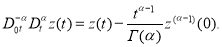
2. Постановка и основной результат

В области рассмотрим начально-краевую задачу

. (2.1)

(2.2)

(2.3)

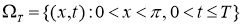
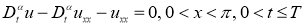
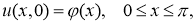
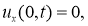
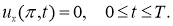
где , заданные функции.

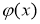
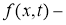
Здесь дробная производная Капуто порядка .

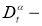
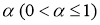
Определение 1. Классическим решением задачи (2.1) -(2.3) в области назовем функцию из класса которая уравнению (2.1) при всех , начальному условию (2.2) при всех , и краевым условиям (2.3) при всех .

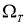
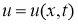
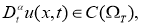
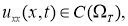
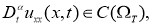
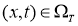
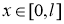
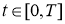
Теорема . Пусть , и Тогда задача (1) -(3) имеет единственное решение. Это решение представимо в виде

(2.4)

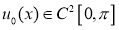
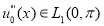
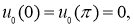
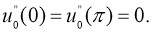
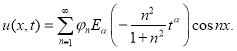
Доказательство. Согласно методу Фурье, нетривиальные решения уравнения (2.1), удовлетворяющее граничным условиям (2.3) ищем в виде

(2.5)

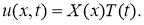
Подставляя значения из (2.4) в (2.1) и разделяя переменные, получим

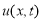
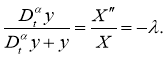
Отсюда, предполагая, что , и учитывая условие (2.3), получим следующие уравнения относительно функций :

(2.6)

(2.7)

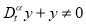
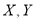
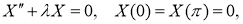
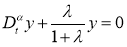
Известно, что задача Штурма-Лиувилля (2.6) имеет следующий вид собственные значения и собственные функции:

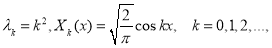
и образуют ортонормированный базис в пространстве

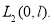
Дифференциальное уравнение дробного порядка (9) при имеет вид

(2.8)

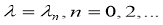
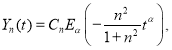
где функция Миттаг-Леффлера, — пока произвольные постоянные.

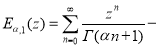
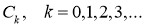
Объединив и получим:

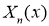
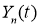
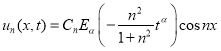
удовлетворяют уравнению (2.1) и граничным условиям (2.3).

Воспользовавшись обобщенным принципом суперпозиции, запишем решение задачи (2.1), (2.3) в виде

(2.9)

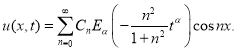
Для нахождения неизвестных постоянных , воспользуемся начальным условием (2.2). Тогда из (2.9) имеем

(2.10)

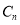
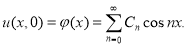
Рассматривая это равенство как разложение в ряд Фурье, найдем коэффициенты Фурье

(2.11)

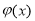
Подставив найденные в (2.9), получим формальное решение задачи

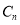
(2.1)-(2.3):

(2.12)

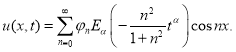
Теперь покажем, что найденная функция является классическим решением задачи (2.1)-(2.3).Сначала покажем непрерывность функции в области . Из условий, наложенных на функции , следует, что

(2.13)

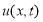
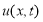
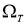
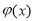
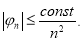
Отсюда следует, что ряд (2.12) с коэффициентами , определяемыми по формулам (2.12), равномерно и абсолютно сходится к функции .

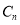
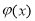
Далее покажем, что формально построенное решение (2.4) является классическим, т. е. регулярным при непрерывным по x при и удовлетворяет дополнительным условиям (2.1), (2.3).

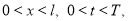
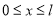
Используя неравенство (2.13) и то, что

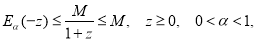
из формулы (2.11), имеем

.(2.14)

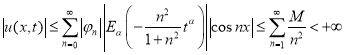
Поэтому функция определяемая рядом (2.12), непрерывна в области и удовлетворяет начальному условию (2.2) и граничным условиям (2.3).

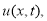
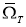
Остается показать, что функция удовлетворяет уравнению (2.1) в области . Для этого достаточно показать равномерную сходимость рядов

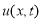
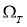
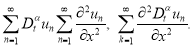
Формально дифференцируя ряд (2.12), находим

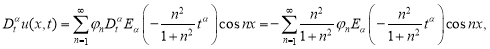
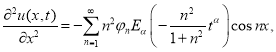
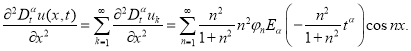
Поскольку

,

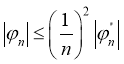
то

(2.15)

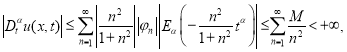
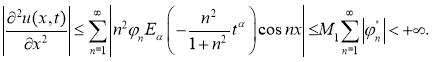
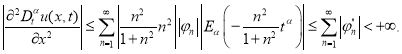
Из оценок (2.15) заключаем, что ряды

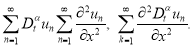
сходятся равномерно к , и соответственно. Теорема доказана.

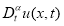
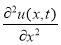
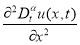
Литература:

1. Kilbas A. A., Srivastava H. M. and Trujillo J. J. “Theory and Applications of Fractional Differential Equations,” North-Holland Mathematics Studies , Vol. 204, 2006.
2. Miller K. S. and. Ross B. “An Introduction to the Frac- tional Calculus and Fractional Differential Equations,” John Wiley, New York, 1993.
3. Podlubny I. “Fractional Differential Equations,” Aca- demic Press, San Diego, New York, London, 1999.
4. Самко С. Г., Килбас А. А., Маричев О. И. Интегралы и производные дробного порядка и некоторые их приложения. — Минск: Наука и техника, 1987. — 688 с.
5. Джарбашян М. М. Интегральные преобразования и представления функций в комплексной области. М., 1966.-672с.
6. Нахушев А. М. Дробное исчисление и его применение. М.: Физматлит, 2003. 272 с.
7. Учайкин В. В. Метод дробных производных. Ульяновск: Артишок, 2008. 512 с.
8. Псху А. В. Уравнения в частных производных дробного порядка. М.: Наука. 2005. 199 с.
9. Аблабеков, Б. С. Обратные задачи для псевдопараболических уравнений.- Бишкек: Илим, 2001. –183 с.
10. Аблабеков, Б. С. Метод полуобращения и существование решений начальной, начально-краевой задачи // Наука и новые технологии. –1999.- № 4. — С. 12– 19.