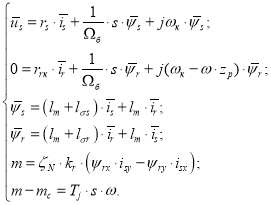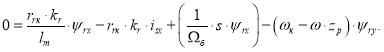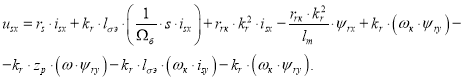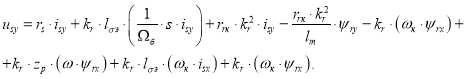В наших статьях за 2015 г. приведены математические модели асинхронного двигателя с переменными ψr и is. Данная работа является модификацией работы [1]: произведены существенные изменения в способе вывода уравнений и выделен базовый вариант.
Так как главной целью является привлечение студентов к исследовательской работе, то в соответствии с нашей традицией, выводы всех уравнений приводим без сокращений.
Векторные уравнения асинхронного двигателя с короткозамкнутым ротором имеют следующий вид:
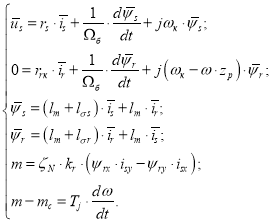
Переводим систему уравнений к изображениям:
![]()
|
|
(1) |
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
Схема замещения и векторная диаграмма переменных [3] приведены на рис. 1 и 2.
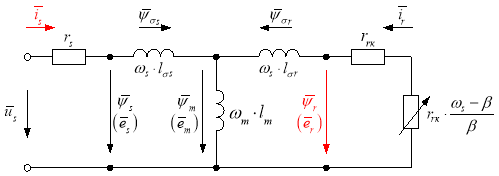
Рис. 1. Связь токов и потокосцеплений в асинхронном двигателе
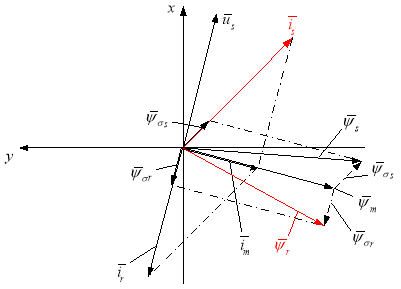
Рис. 2. Качественная картина расположения векторов в двигательном режиме асинхронного двигателя
Разложение векторных величин по проекциям:
![]()
![]()
![]()
![]()
![]()
Записываем уравнения (1) – (4) по проекциям.
Уравнение (1):
![]()
|
По оси (+1): |
|
(1’) |
|
По оси (+j): |
|
(1”) |
Уравнение (2):
![]()
|
По оси (+1): |
|
(2’) |
|
По оси (+j): |
|
(2”) |
Уравнение (3):
![]()
|
По оси (+1): |
|
(3’) |
|
По оси (+j): |
|
(3”) |
Уравнение (4):
|
По оси (+1): |
|
(4’) |
|
По оси (+j): |
|
(4”) |
Так как электромагнитный момент определяется через две переменные is и ψr, то из уравнений (1’), …, (4’) необходимо исключить переменные ir и ψs.
Из уравнения (4’) выразим irx:
![]()
Обозначим ![]() тогда:
тогда:
|
|
(7) |
Из уравнения (4”) выразим iry:
![]()
|
|
(8) |
Подставим уравнение (7) в (3’):
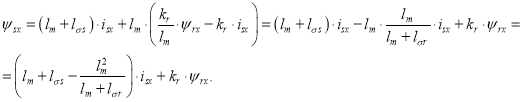
Обозначим ![]() :
:
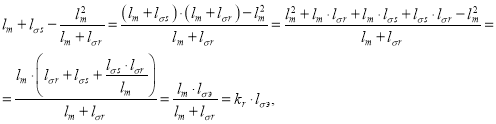
где
Отсюда потокосцепление ψsx определится следующим образом:
|
|
(9) |
Подставим (8) в (3”):
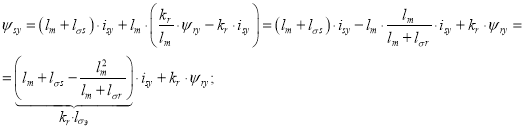
|
|
(10) |
Полученные зависимости рассмотрим в единой системе по проекции x (+1):
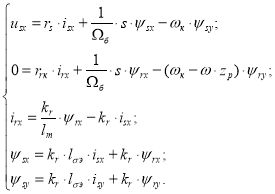
Подставим уравнение (7) в (2’):
|
|
(11) |
Из уравнения (11) определим ![]() , которое нам понадобится в дальнейшем:
, которое нам понадобится в дальнейшем:
|
|
(12) |
Для получения апериодического звена перенесем слагаемые с ψrx в левую часть:
![]()
Умножим обе части полученного уравнения на lm:
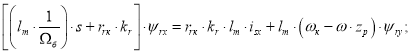
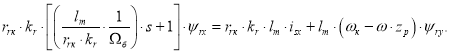
Обозначим ![]()
Отсюда ψrx определится в следующей форме:
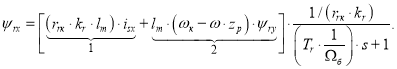
Структурная схема для определения потокосцепления ψrx приведена на рис. 3.

Рис. 3. Структурная схема для определения потокосцепления ψrx
Подставим выражения ψsx и ψsy из уравнений (9) и (10) в уравнение (1’):
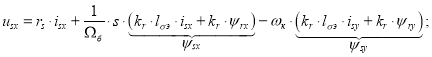
![]()
В полученное уравнение подставим выражение
|
|
(13) |
Перенесем слагаемые с переменными isx в левую часть:
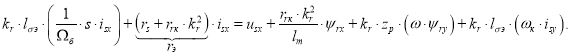
Обозначим ![]() и
и ![]() :
:
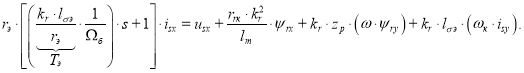
Тогда isx определится в следующей форме:
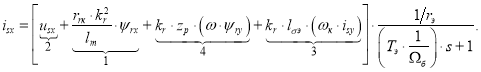
Структурная схема для определения тока isx дана на рис. 4.
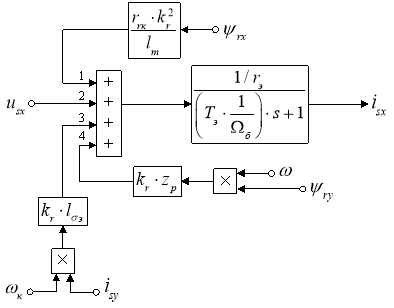
Рис. 4. Структурная схема для определения тока isx
Аналогично, система уравнений по проекции y (+j):
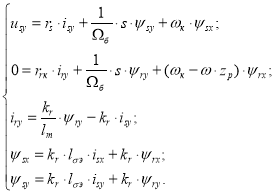
Подставим уравнение (8) в (2”):
|
|
(14) |
Из уравнения (14) выразим ![]() :
:
|
|
(15) |
Для получения апериодического звена перенесем слагаемые с ψry в левую часть:
![]()
Умножим обе части полученного уравнения на lm и вынесем за скобки ![]() :
:
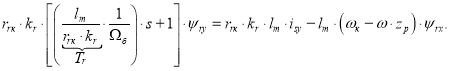
Отсюда ψry определится в следующей форме:
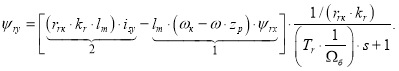
Структурная схема для определения потокосцепления ψry приведена на рис. 5.

Рис. 5. Структурная схема для определения потокосцепления ψry
Для определения isy подставим уравнения (9) и (10) в (1”):
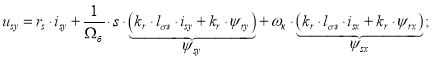
![]()
Подставим ![]() из (15) в полученное уравнение:
из (15) в полученное уравнение:
|
|
(16) |
Перенесем слагаемые с переменными isy в левую часть:
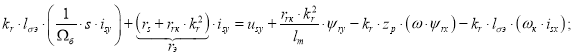
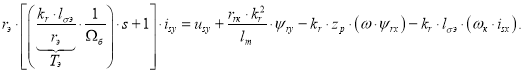
Ток isy определится в следующей форме:
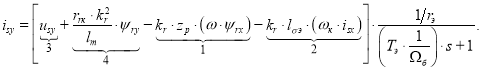
Структурная схема для определения isy приведена на рис. 6.
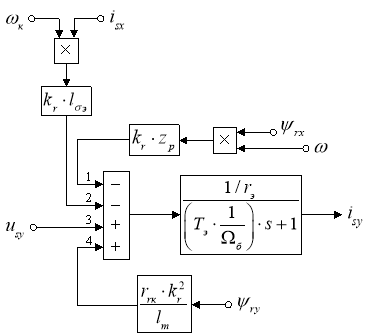
Рис. 6. Структурная схема для определения тока isy
На рис. 7 представлена структурная схема для реализации уравнения электромагнитного момента (5):
![]()
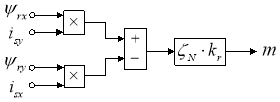
Рис. 7. Математическая модель определения электромагнитного момента m
Наконец, из уравнения движения (6) выразим механическую угловую скорость вращения вала двигателя (рис. 8):
![]()
![]()

Рис. 8. Математическая модель уравнения движения
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными is – ψr на выходе апериодических звеньев приведена на рис. 9. Параметры асинхронного двигателя рассмотрены в работах [2] и [3].
Расчет параметров производим в Script:
|
PN=320000; UsN=380; IsN=324; fN=50; Omega0N=104.7; OmegaN=102.83; nN=0.944; cos_phiN=0.92; zp=3; Rs=0.0178; Xs=0.118; Rr=0.0194; Xr=0.123; Xm=4.552; |
J=28; Ub=sqrt(2)*UsN; Ib=sqrt(2)*IsN; OmegasN=2*pi*fN; Omegab=OmegasN; Omegarb=Omegab/zp; Zb=Ub/Ib; Psib=Ub/Omegab; Lb=Psib/Ib; kd=1.0084; Mb=kd*PN/OmegaN; Pb=Mb*Omegarb; rs=Rs/Zb; lbs=Xs/Zb; |
rr=Rr/Zb; lbr=Xr/Zb; lm=Xm/Zb; Tj=J*Omegarb/Mb; betaN=(Omega0N-OmegaN)/Omega0N; SsN=3*UsN*IsN; ZetaN=SsN/Pb; ks=lm/(lm+lbs); kr=lm/(lm+lbr); lbe=lbs+lbr+lbs*lbr*lm^(-1); roN=0.9962; rrk=roN*betaN; Tr=lm/(rrk*kr); re=rs+rrk*kr^2; Te=kr*lbe/re; |
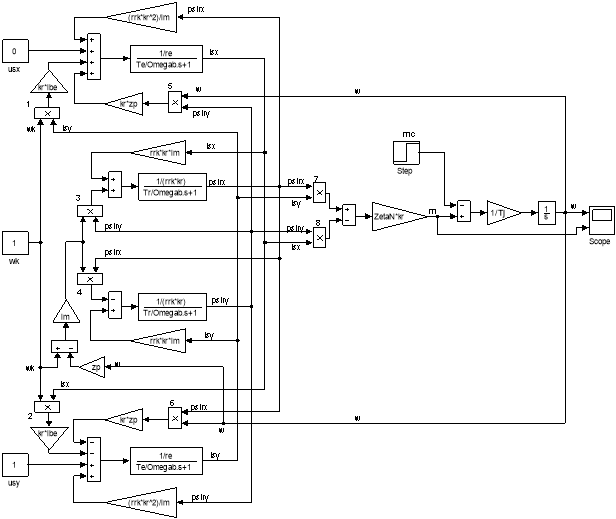
Рис. 9. Математическая модель асинхронного двигателя с переменными is – ψr на выходе апериодических звеньев
Результаты моделирования асинхронного двигателя представлены на рис. 10.
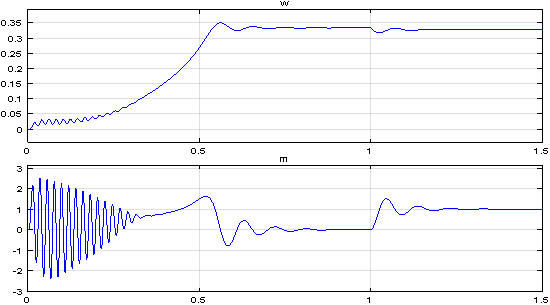
Рис. 10. Графики скорости и момента
Литература:
- Емельянов А.А., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Королев О.А. Математическая модель асинхронного двигателя с переменными ψr - Ir в произвольной системе координат // Молодой ученый. - 2015. - №13. - С. 7-20.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. - 654 с.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.