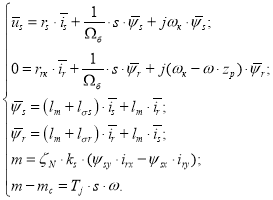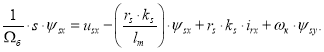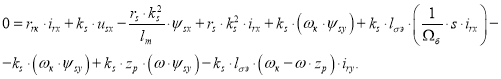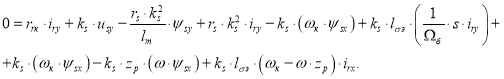Данная работа является продолжением статьи [1], в которой были подробно даны способы и технологии получения пространственных векторов. В работах [2] и [3] приведено множество вариантов определения электромагнитных моментов комбинацией двух переменных (ψr – is, ψs – is, ψs – ψr и т.д.).
В наших статьях за 2015 г. приведены математические модели с переменными ψr и is. В этой работе рассмотрим моделирование асинхронного двигателя с короткозамкнутым ротором с переменными ir и ψs. Так как главной целью является привлечение студентов к исследовательской работе, то в соответствии с нашей традицией, выводы всех уравнений приводим без сокращений.
Векторные уравнения асинхронного двигателя с короткозамкнутым ротором имеют следующий вид:
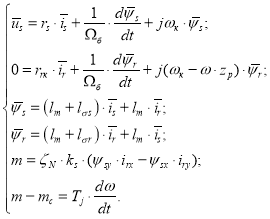
Переводим систему уравнений к изображениям ![]() :
:
|
|
(1) |
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
Схема замещения и векторная диаграмма переменных [3] приведены на рис. 1 и 2.
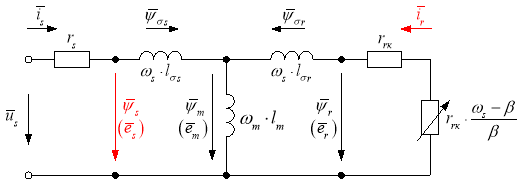
Рис. 1. Связь токов и потокосцеплений в асинхронном двигателе
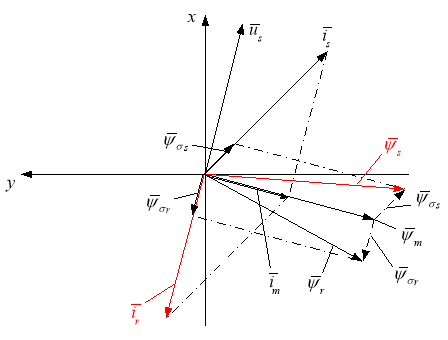
Рис. 2. Качественная картина расположения векторов в двигательном режиме асинхронного двигателя
Разложение векторных величин по проекциям:
![]()
![]()
![]()
![]()
![]()
Записываем уравнения (1), …, (4) по проекциям.
Уравнение (1):
![]()
|
По оси (+1): |
|
(1’) |
|
По оси (+j): |
|
(1”) |
Уравнение (2):
![]()
|
По оси (+1): |
|
(2’) |
|
По оси (+j): |
|
(2”) |
Уравнение (3):
![]()
|
По оси (+1): |
|
(3’) |
|
По оси (+j): |
|
(3”) |
Уравнение (4):
![]()
|
По оси (+1): |
|
(4’) |
|
По оси (+j): |
|
(4”) |
Так как электромагнитный момент определяется через две переменные ir и ψs, то из уравнений (1’), …, (4’) необходимо исключить переменные is и ψr.
Из уравнения (3’) выразим isx:
![]()
Обозначим ![]() тогда:
тогда:
|
|
(5’) |
Подставим уравнение (5’) в (4’):
![]()
Обозначим ![]() :
:
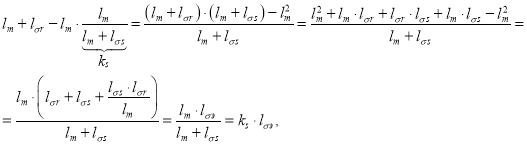
Где ![]()
Отсюда потокосцепление ψrx определится следующим образом:
|
|
(6’) |
Определим isy и ψry из уравнений (3”) и (4”):
![]()
Из уравнения (3”):
![]()
|
|
(5”) |
Подставим (5”) в (4”):
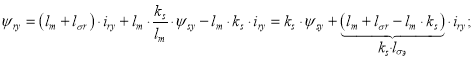
|
|
(6”) |
Полученные зависимости рассмотрим в единой системе по проекции x (+1):
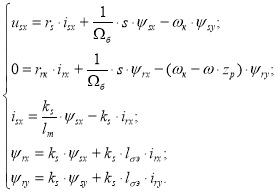
Подставим уравнение (5’) в уравнение (1’):
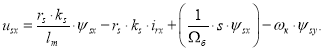
Определим ![]() , которое нам понадобится в дальнейшем:
, которое нам понадобится в дальнейшем:
|
|
(7’) |
Для получения апериодического звена вынесем в левую часть слагаемое
![]()
Умножим обе части на ![]() и вынесем за скобки
и вынесем за скобки ![]() :
:
![]()
Обозначим ![]() и
и ![]()
Тогда ψsx определится в следующей форме:
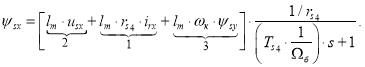
Структурная схема для определения потокосцепления ψsx приведена на рис. 3.
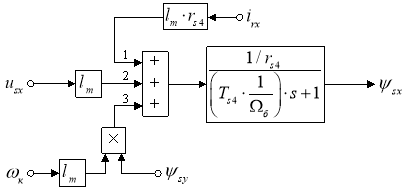
Рис. 3. Структурная схема для определения потокосцепления ψsx
Подставим выражения ψrx и ψry из уравнений (6’) и (6”) в уравнение (2’):
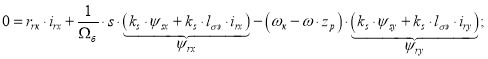
![]()
В полученное уравнение подставим выражение ![]() из уравнения (7’):
из уравнения (7’):
|
|
(8’) |
Перенесем слагаемые с переменными irx в левую часть:
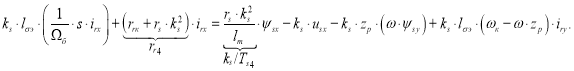
Обозначим ![]()
![]() и
и ![]() .
.
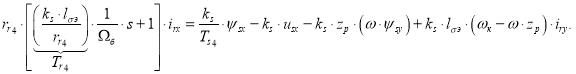
Тогда irx определится в следующей форме:
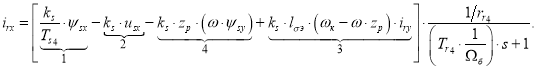
Структурная схема для определения тока irx дана на рис. 4.
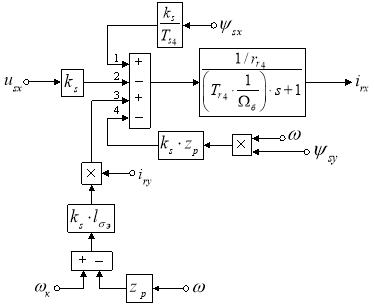
Рис. 4. Структурная схема для определения тока irx
Рассмотрим систему уравнений по проекции y (+j):
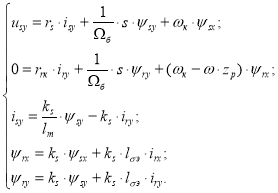
Подставим уравнение (5”) в уравнение (1”):
![]()
Определим ![]() , которое нам понадобится в дальнейшем:
, которое нам понадобится в дальнейшем:
|
|
(7”) |
Для получения апериодического звена вынесем ![]() в левую часть:
в левую часть:
![]()
Умножим обе части на ![]() и вынесем за скобки
и вынесем за скобки ![]() :
:
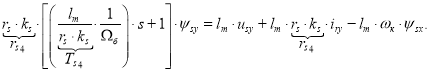
Отсюда ψsy определится в следующей форме:
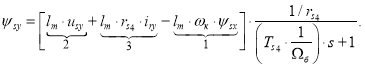
Структурная схема для определения потокосцепления ψsy приведена на рис. 5.
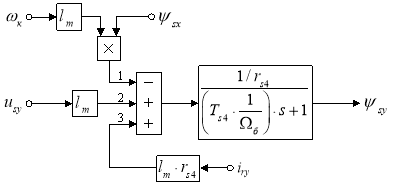
Рис. 5. Структурная схема для определения потокосцепления ψsy
Для определения iry подставим уравнения (6”) и (6’) в уравнение (2”):
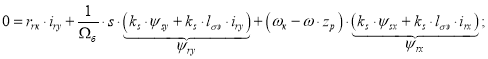
![]()
Подставим в полученное уравнение выражение ![]() из (7”):
из (7”):
|
|
(8”) |
Перенесем слагаемые с переменными iry в левую часть:
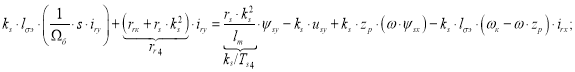
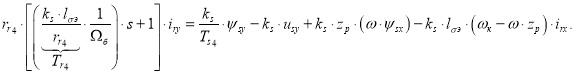
Ток iry определится в следующей форме:
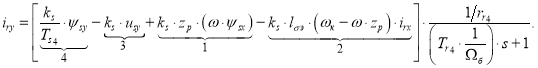
Структурная схема для определения iry приведена на рис. 6.
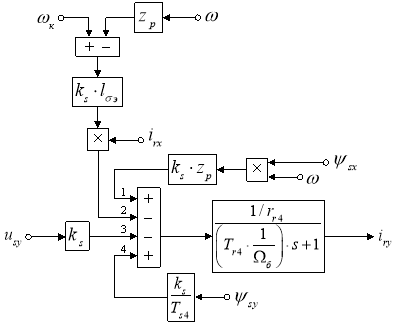
Рис. 6. Структурная схема для определения тока iry
На рис. 7 представлена структурная схема для реализации уравнения электромагнитного момента (5):
![]()
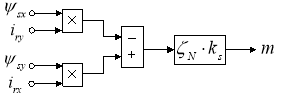
Рис. 7. Математическая модель определения электромагнитного момента m
Наконец, из уравнения движения (6) выразим механическую угловую скорость вращения вала двигателя:
![]()
Структурная схема дана на рис. 8.
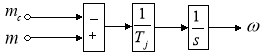
Рис. 8. Математическая модель уравнения движения
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными ir – ψs на выходе апериодических звеньев приведена на рис. 9.
Расчет параметров производим в Script:
|
PN=320000; UsN=380; IsN=324; fN=50; Omega0N=104.7; OmegaN=102.83; nN=0.944; cos_phiN=0.92; zp=3; Rs=0.0178; Xs=0.118; Rr=0.0194; Xr=0.123; Xm=4.552; J=28; |
Ub=sqrt(2)*UsN; Ib=sqrt(2)*IsN; OmegasN=2*pi*fN; Omegab=OmegasN; Omegarb=Omegab/zp; Zb=Ub/Ib; Psib=Ub/Omegab; Lb=Psib/Ib; kd=1.0084; Mb=kd*PN/OmegaN; Pb=Mb*Omegarb; rs=Rs/Zb; lbs=Xs/Zb; rr=Rr/Zb; lbr=Xr/Zb; |
lm=Xm/Zb; Tj=J*Omegarb/Mb; betaN=(Omega0N-OmegaN)/Omega0N; SsN=3*UsN*IsN; ZetaN=SsN/Pb; ks=lm/(lm+lbs); kr=lm/(lm+lbr); lbe=lbs+lbr+lbs*lbr*lm^(-1); roN=0.9962; rrk=roN*betaN; rs4=rs*ks; rr4=rrk+rs*ks^2; Ts4=lm/rs4; Tr4=ks*lbe/rr4; |
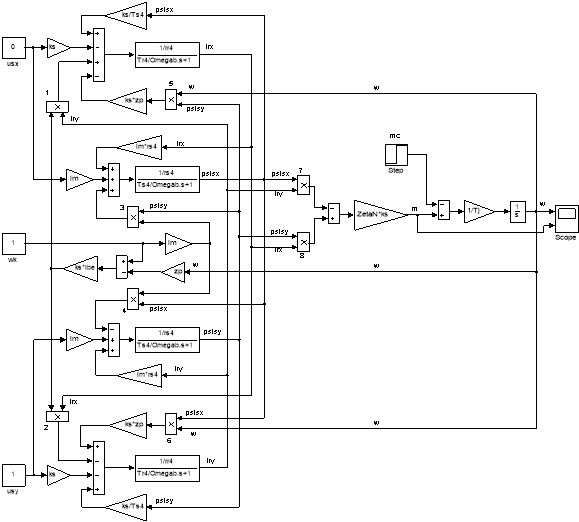
Рис. 9. Математическая модель асинхронного двигателя с переменными ir – ψs на выходе апериодических звеньев
Результаты моделирования асинхронного двигателя представлены на рис. 10.
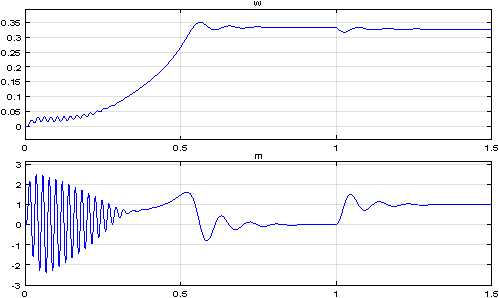
Рис. 10. Графики скорости и момента
Литература:
- Емельянов А. А., Козлов А. М., Бесклеткин В. В., Авдеев А. С., Чернов М. В., Киряков Г. А., Габзалилов Э. Ф., Фуртиков К. А., Реутов А. Я., Королев О. А. Пространственные векторы в асинхронном двигателе в относительной системе единиц // Молодой ученый. – 2015. – №11. – С. 133-156.
- Шрейнер Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. – 654 с.
- Шрейнер Р. Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р. Т. Шрейнер, А. В. Костылев, В. К. Кривовяз, С. И. Шилин. Под ред. проф. д. т. н. Р. Т. Шрейнера. – Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. – 361 с.