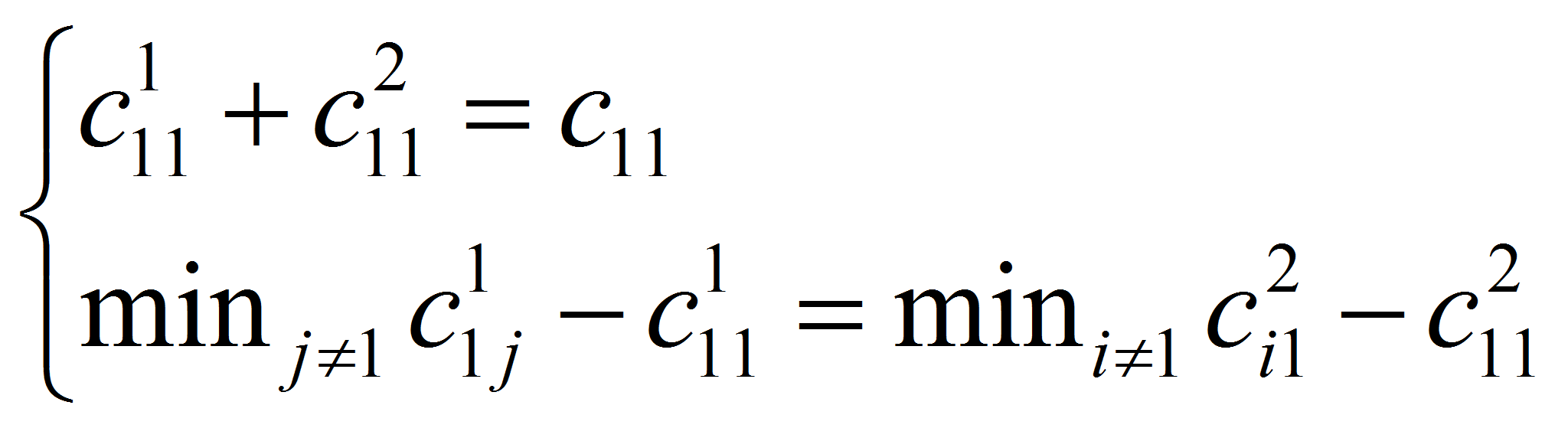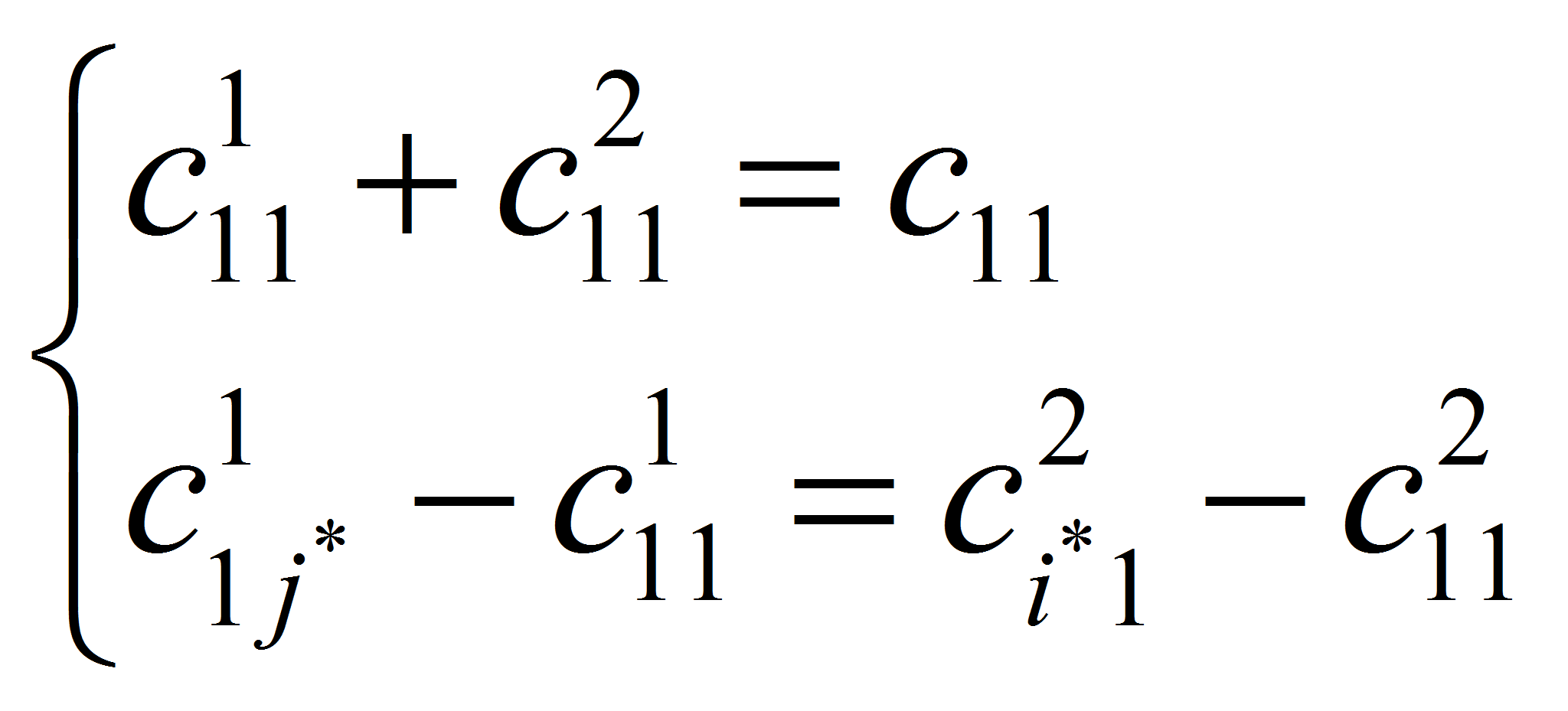Итеративный алгоритм для задачи о назначении

Предложен новый метод решения задачи о назначении, основанный на декомпозиции исходной задачи на ряд двумерных оптимизационных задач. Целочисленность и монотонность по целевой функции итерационного процесса решения обеспечивает конечность алгоритма. В результате может получиться или единственное оптимальное решение исходной задачи о назначении, или система ограничений, из которой можно получить все оптимальные решения.

Введение. В данной работе метод последовательных изменений параметров функционала для транспортных задач [1] конкретизируется для задачи о назначении (см., например, [2]). Специфика задачи о назначении выявляет особенности применения данного алгоритма. Булевость переменных приводит к более простым формулам, а интерпретация при вырождении является более прозрачной.

1. Предварительные рассмотрения. Имеется следующая классическая задача о назначении (см., например, [2]):

(1.1)

(1.2)

(1.3)

-целые, , (1.4)

Предположим, что 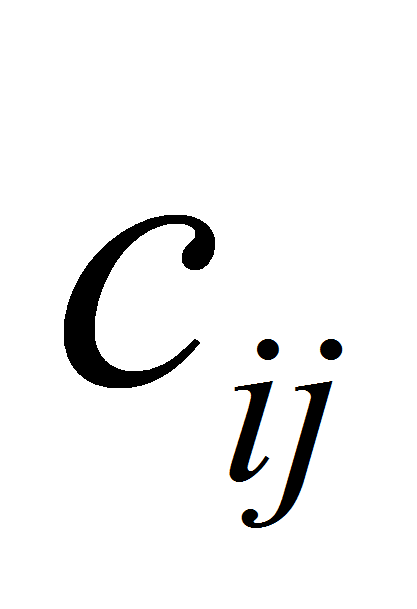- чётные неотрицательные числа при всех 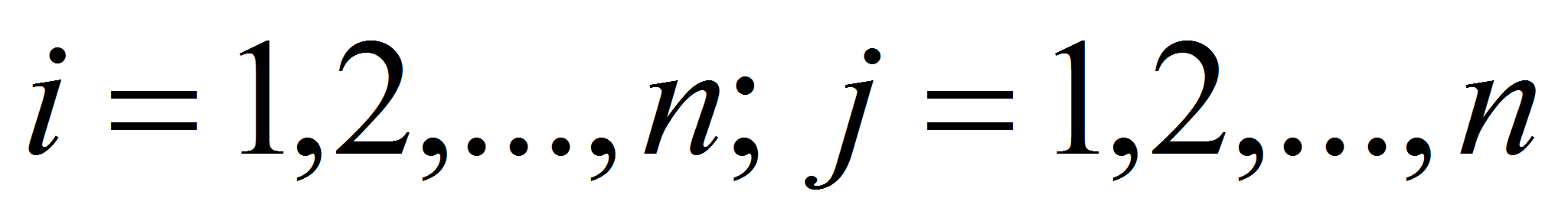, что не ограничивает общности рассмотрения.

Здесь используется известная интерпретация. Имеются 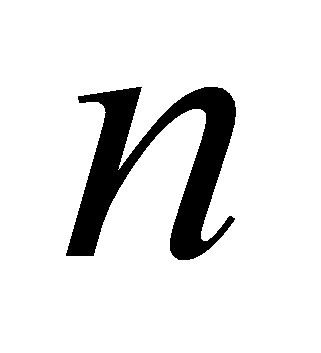работ и 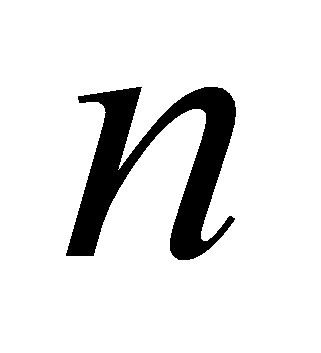исполнителей. 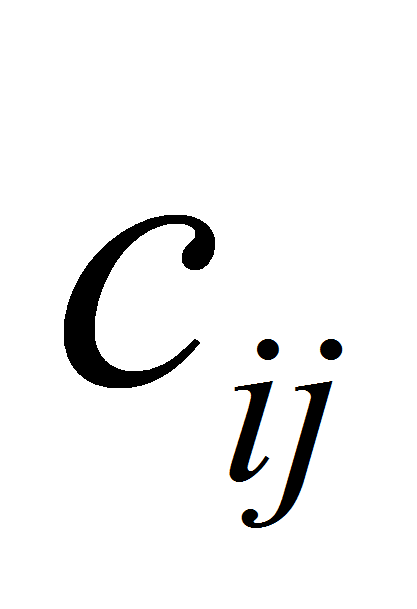- количество рабочих часов, которые затрачивает 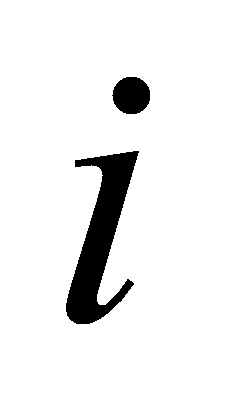-й исполнитель на 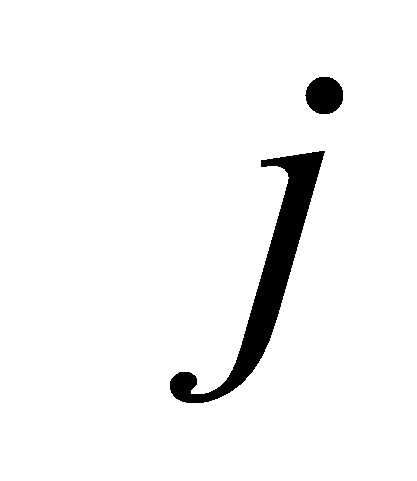-ю работу. Целью является минимизация суммы рабочего времени на выполнение всех 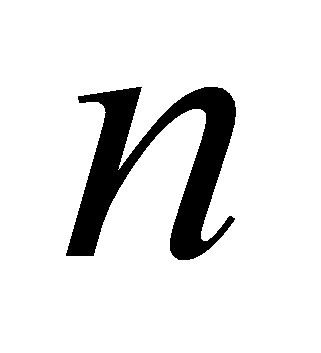работ .

Вычислим и составим оптимизационных задач с ограничениями (1.1):

; (1.5)

-целые, , (1.6)

Составим также ещё оптимизационных задач с ограничениями (1.2) и (1.6):

(1.7)

Задачи вида (1.1), (1.5), (1.6), и (1.2), (1.6), (1.7) решаются простым выбором наименьших коэффициентов целевой функции, а именно, пусть в задаче вида (1.1), (1.5), (1.6)

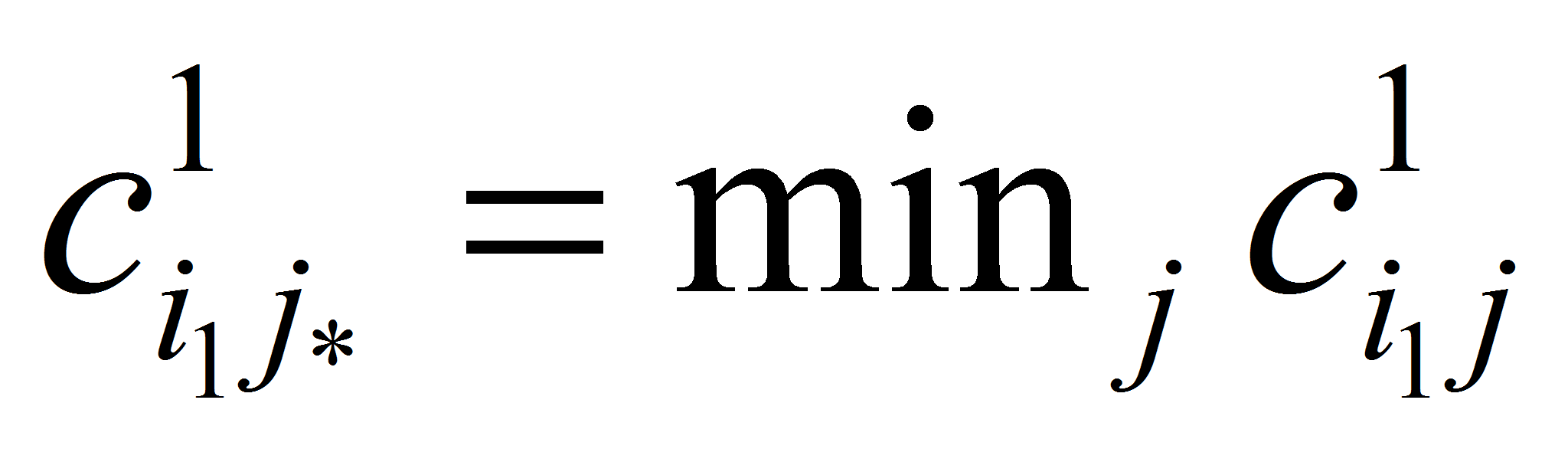, тогда

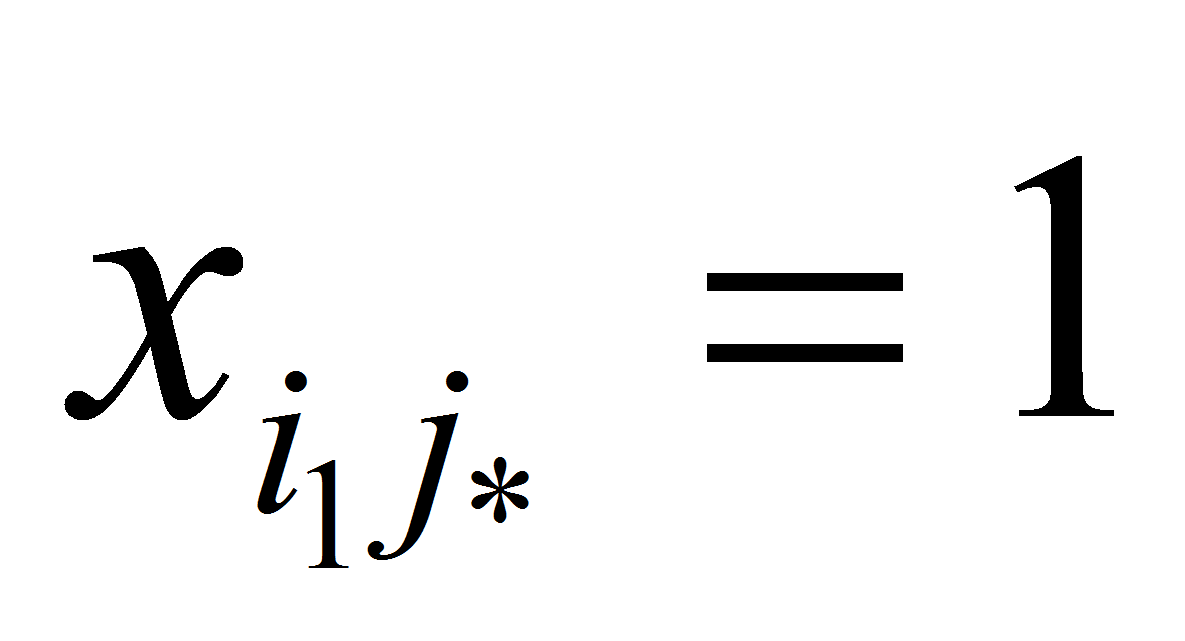
Точно так же решаются и задачи (1.2), (1.6), (1.7).

Предположим, что все 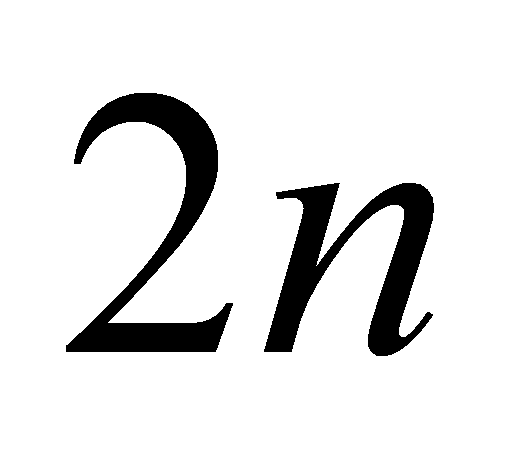задач (1.1), (1.5), (1.6) и (1.2), (1.6), (1.7) решены. Объединение оптимальных решений всех 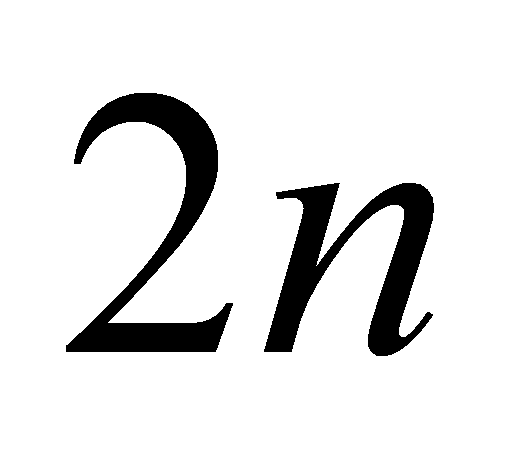одномерных задач назовём псевдорешением исходной задачи о назначении, а соответствующую сумму значений целевых функций значением целевой функции псевдорешения. Очевидно, что значение целевой функции псевдорешения не превосходит значения целевой функции оптимального решения исходной задачи (1.1) – (1.4), причём этот факт не зависит от способа разбиения каждого 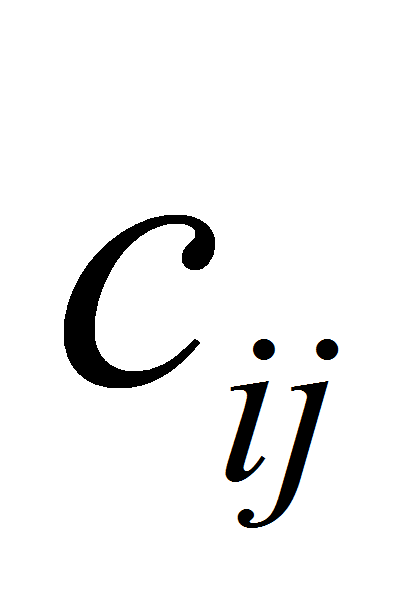на два слагаемых.

Теорема 1. Если объединение оптимальных решений всех 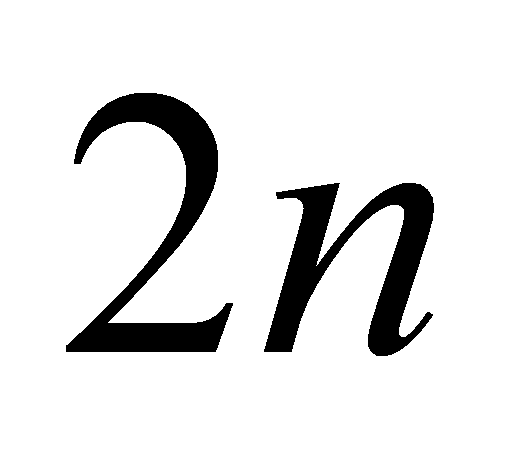задач (1.1), (1.5), (1.6) и (1.2), (1.6), (1.7) - (псевдорешение исходной задачи о назначении) является допустимым решением задачи исходной задачи (1.1) – (1.4), то оно является оптимальным решением задачи (1.1) – (1.4).

2. Конструкции алгоритма. Пусть объединение оптимальных решений задач (1.1), (1.5), (1.6) и (1.2), (1.6), (1.7) не является допустимым решением исходной задачи (1.1) – (1.4). В этом случае строим пошаговый процесс решения следующих двумерных оптимизационных задач. На первом шаге выпишем первое ограничение из (1.1), (), и первое ограничение из (1.2), ():

(2.1)

(2.2)

Составим целевую функцию:

.(2.3)

и рассмотрим задачу (1.6), (2.1) – (2.3).

При решении задачи (1.6), (2.1) – (2.3) могут иметь место три случая.

Первый случай:

(2.4)

Тогда полагаем и задача (1.6), (2.1) – (2.3) решена. После решения задачи (1.6), (2.1) – (2.3) найдём новые и сначала из системы уравнений

Затем, при необходимости, округлим до ближайшего целого в меньшую сторону, а - в большую сторону.

Второй случай:

Пусть

(2.5)

Тогда обозначим и , вместо решения выписываем ограничения, . Вычисляем новые значения и .

Третий случай:

(2.6)

Тогда, очевидно, что , и задача (1.6), (2.1) – (2.3) решена. Далее, найдём новые и из системы уравнений

Округлим до целого так же, как и во втором случае. Сформируем с новыми значениями и две одномерные задачи. Первая задача

(2.7)

при ограничениях (1.6), (2.1) и вторая задача

(2.8)

при ограничениях (1.6), (2.2).

Имеет место следующее утверждение.

Теорема 2. Во всех вышеперечисленных случаях (выполняется соотношение (2.4), (2.5) или (2.6)) объединение оптимальных решений одномерных задач (1.6), (2.1), (2.7) и (1.6), (2.2), (2.8) с новыми значениями и является оптимальным решением двумерной задачи (1.6), (2.1) – (2.3).

Теорема 3. Объединение решений одномерных задач является оптимальным решением исходной задачи о назначении (1.1) – (1.4).

Теорема 4. Любое допустимое решение редуцированной задачи о назначении, полученной в результате пошагового процесса есть её оптимальное решение.

Итак, оптимальное решение исходной задачи о назначении есть объединение значений переменных, определённых однозначно в итоге пошагового процесса с произвольным допустимым решением редуцированной задачи о назначении.

Рассмотрим, наконец, случай когда в результате пошагового процесса для некоторых переменных в одной из одномерных задач получено некоторое значение, а в другой – ограничение совместно с другими переменными. В этом случае допустимое решение исходной задачи может быть ещё не достигнуто. Возможна ситуация, когда система итоговых ограничений формирует ограничения задачи о назначении с запретами, которая может не иметь допустимых решений. Это будет рассмотрено после примера 1. Верно, однако, следующее утверждение.

Лемма. Оптимальное решение задачи о назначении не изменится, если при сохранении неотрицательности продолжительности выполнения работ изменить на одну и ту же величину все продолжительности выполнения работ одного исполнителя или продолжительность выполнения одной работы всеми исполнителями.

Дальнейшие конструкции алгоритма будут использовать результаты леммы. Они направлены на увеличение количества переменных, входящих в ограничения за счёт переменных с найденным значением. В итоге все переменные окажутся записанными в ограничениях или же оставшиеся переменные с найденным значением не нарушают допустимого решения исходной задачи.

Итак, пусть в результате пошагового процесса допустимое решение исходной задачи о назначении (оно же и оптимальное) не получено. Пусть, для простоты и определённости превышено ограничение первой группы с номером 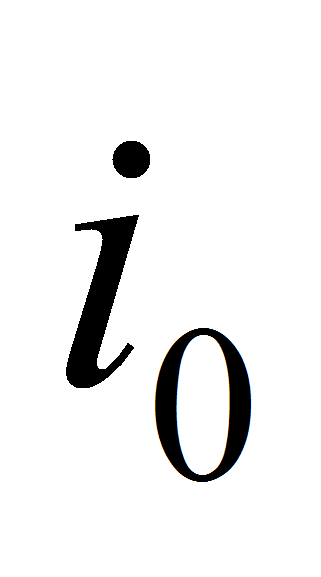, в котором имеет место

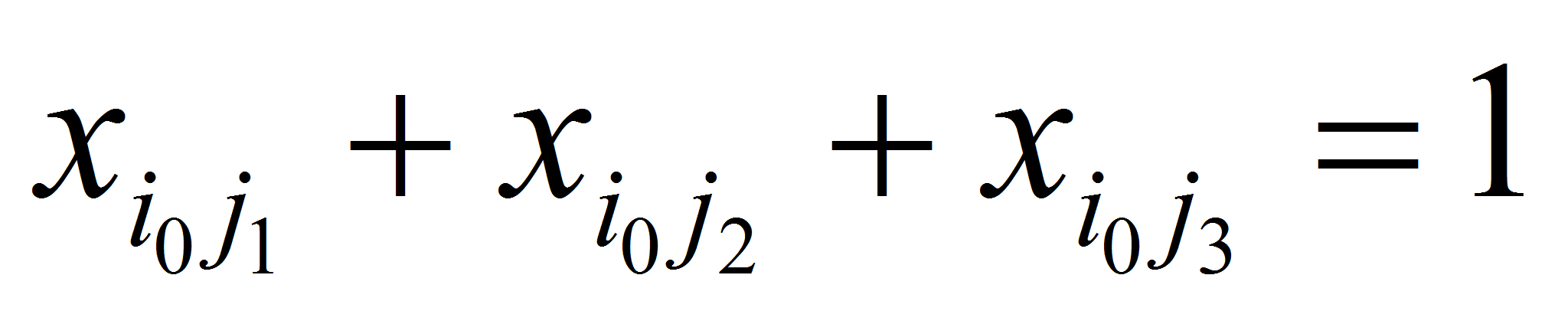, но в ограничениях второй группы имеют место равенства

, , ,

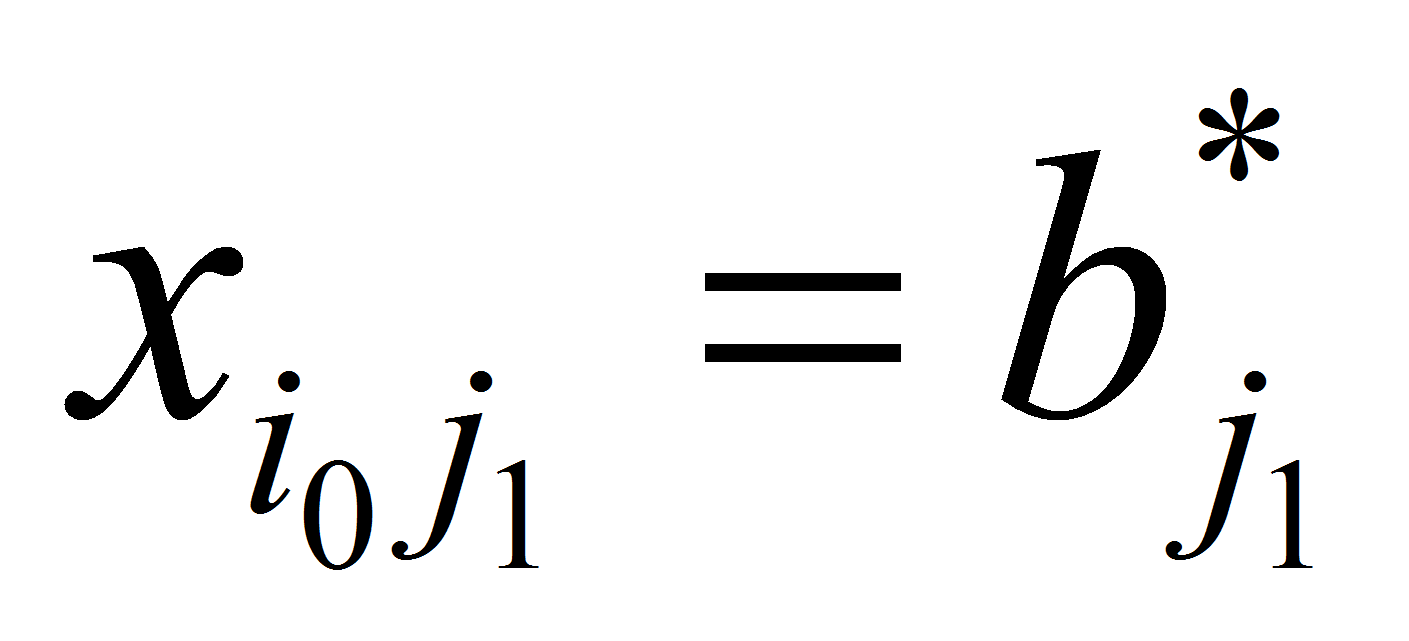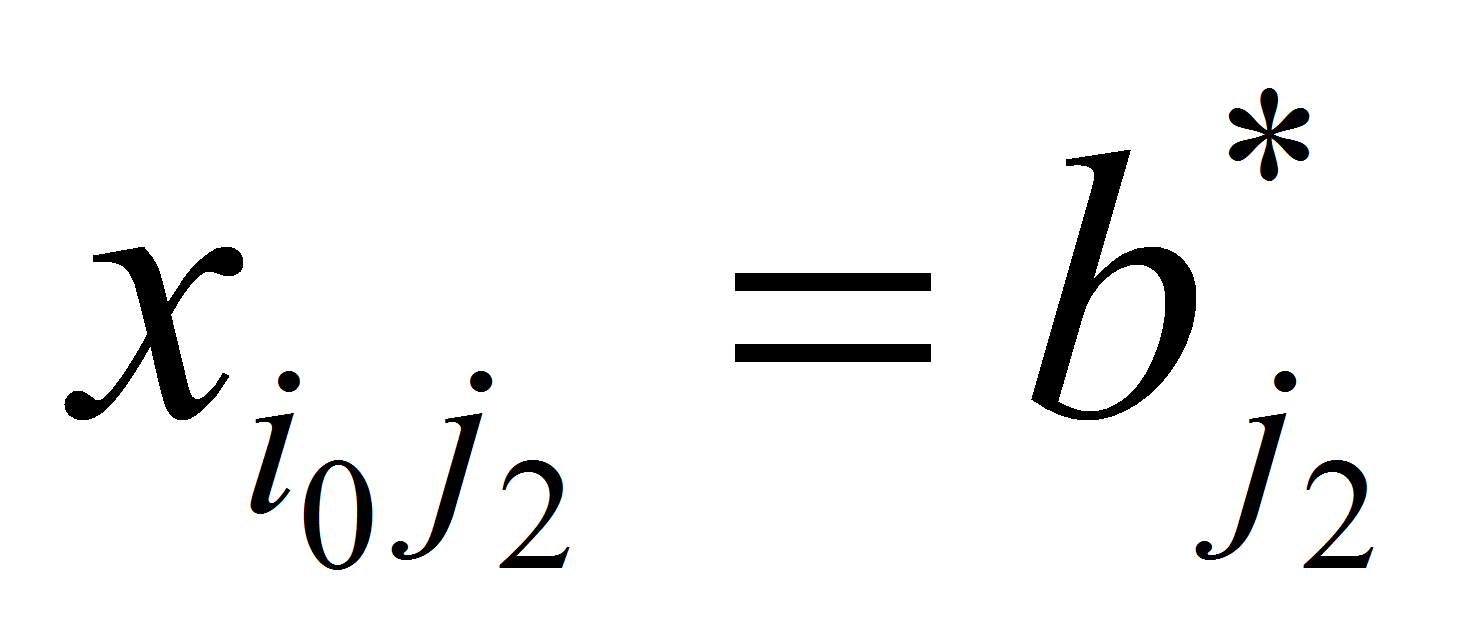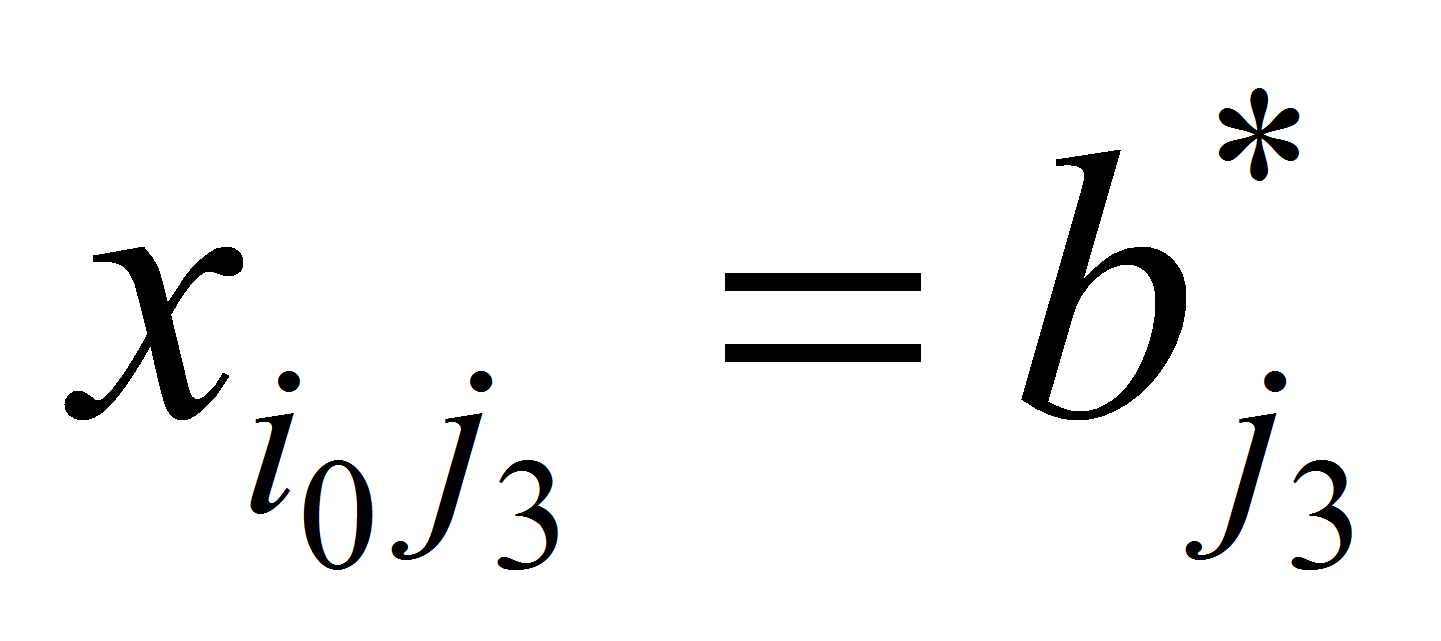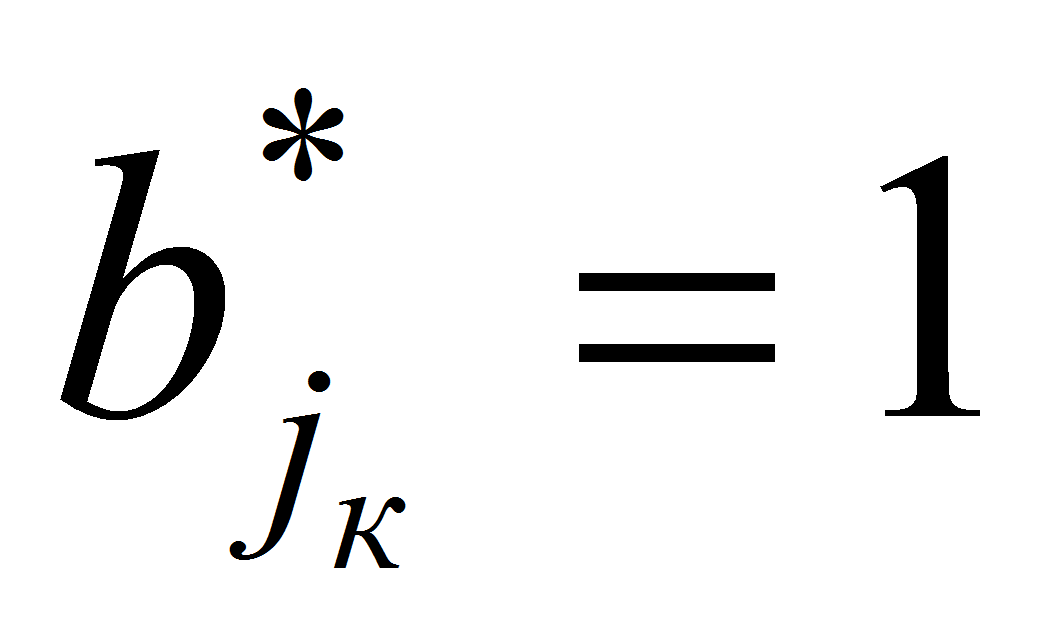
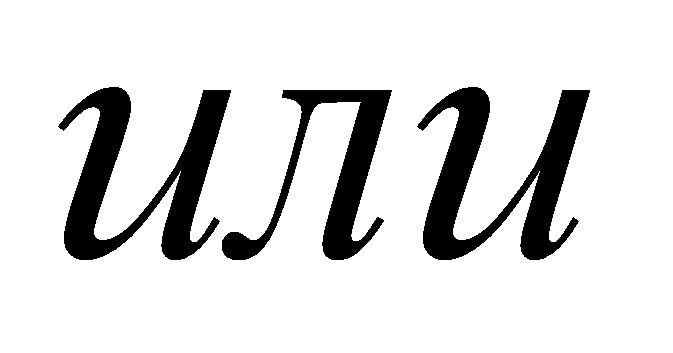
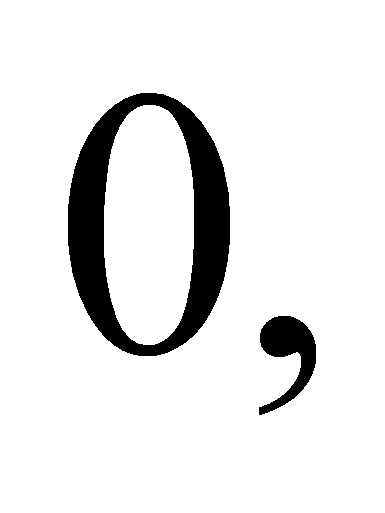
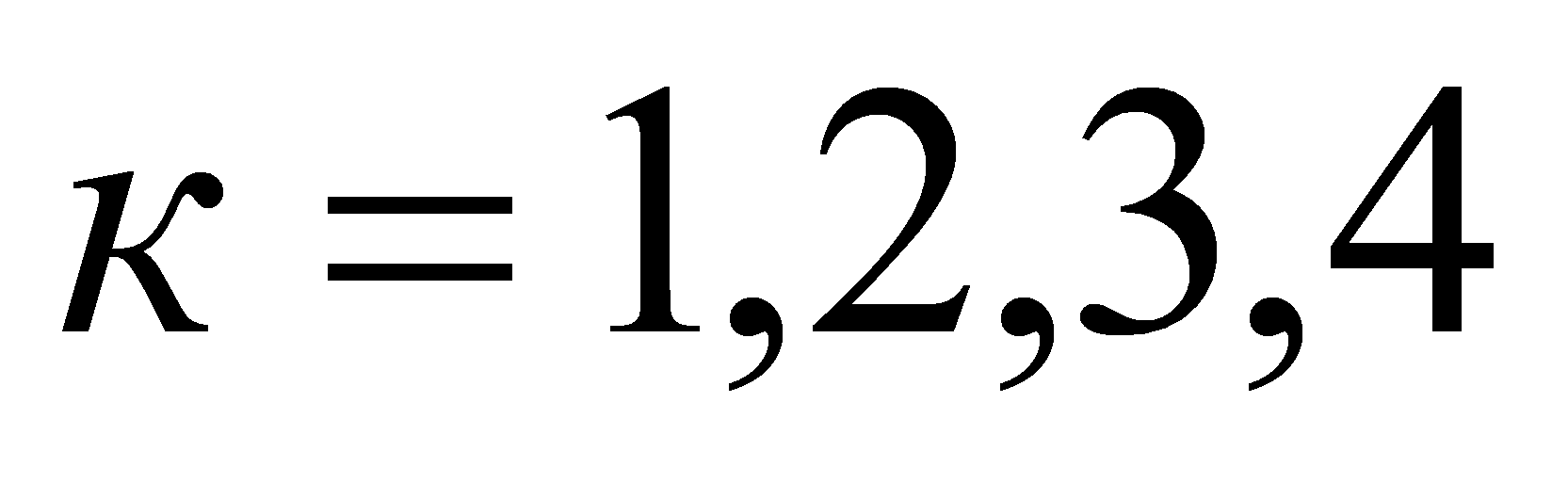
и, кроме того

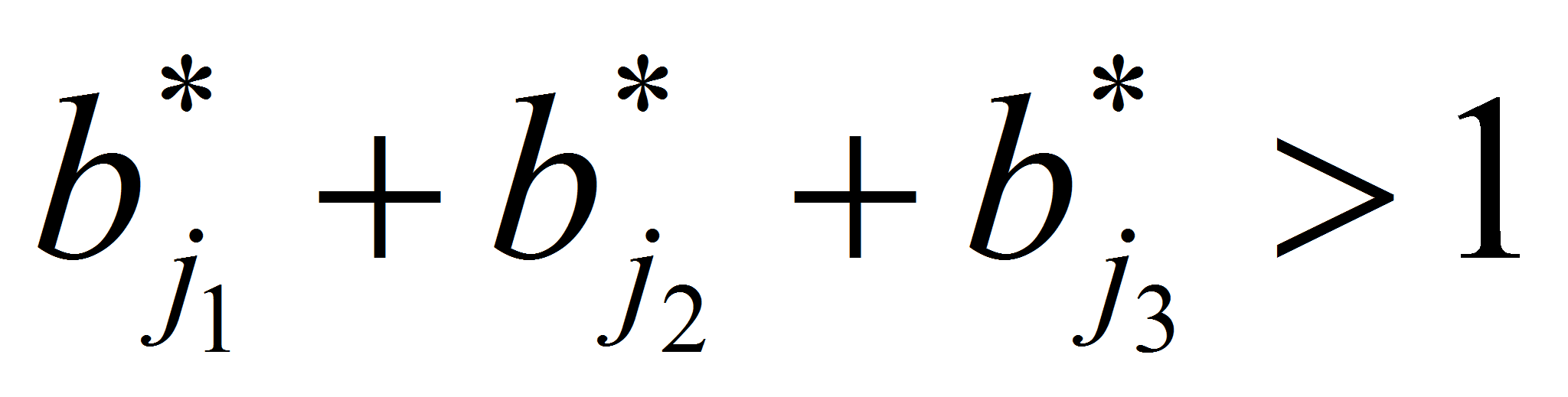. (2.9)

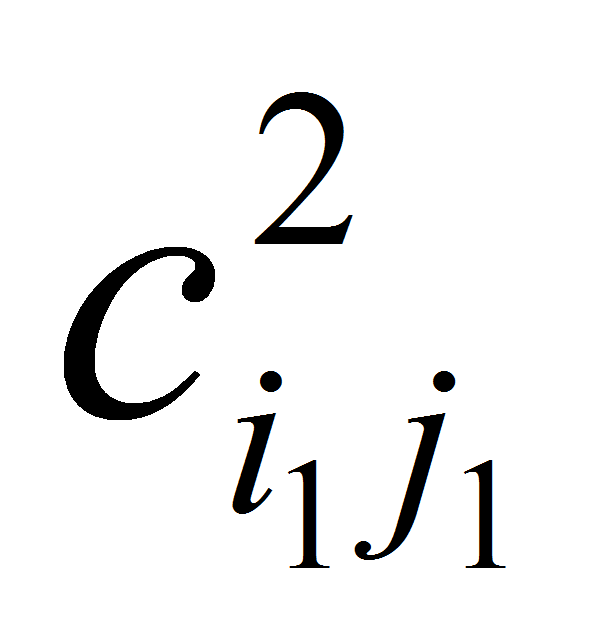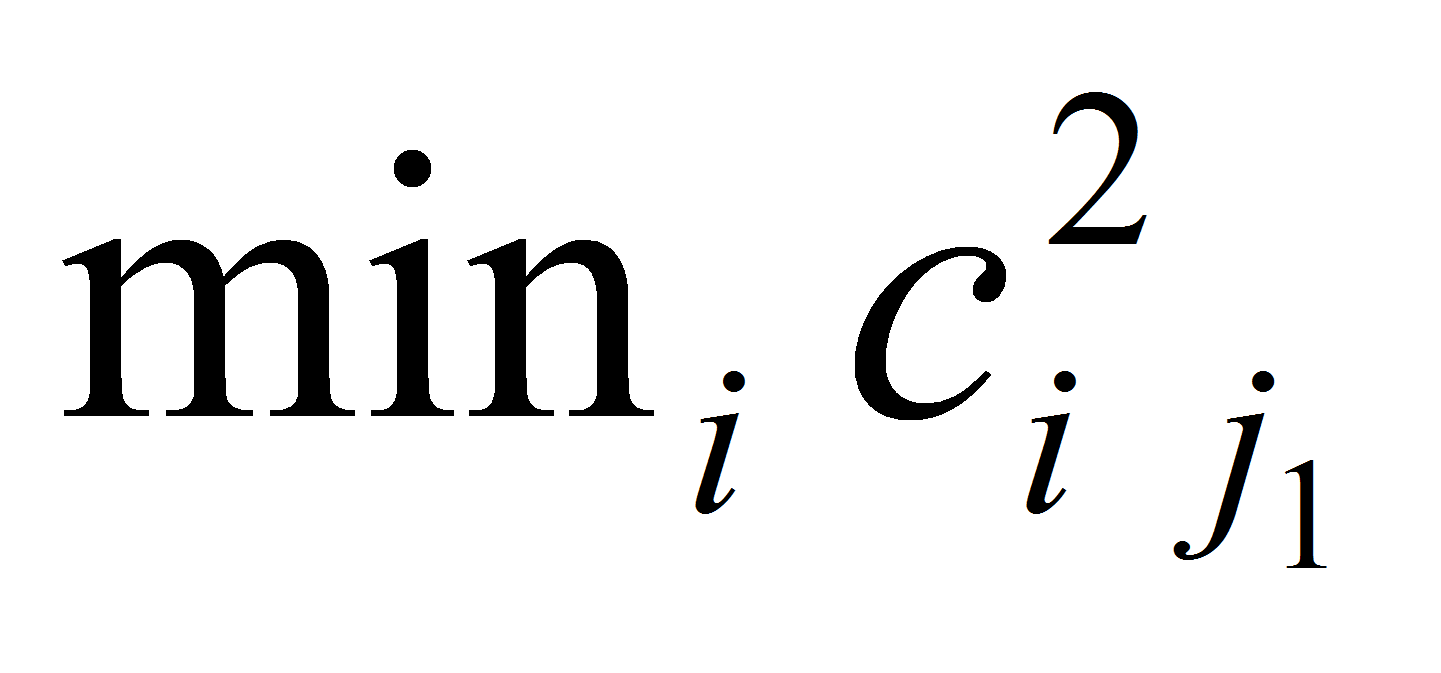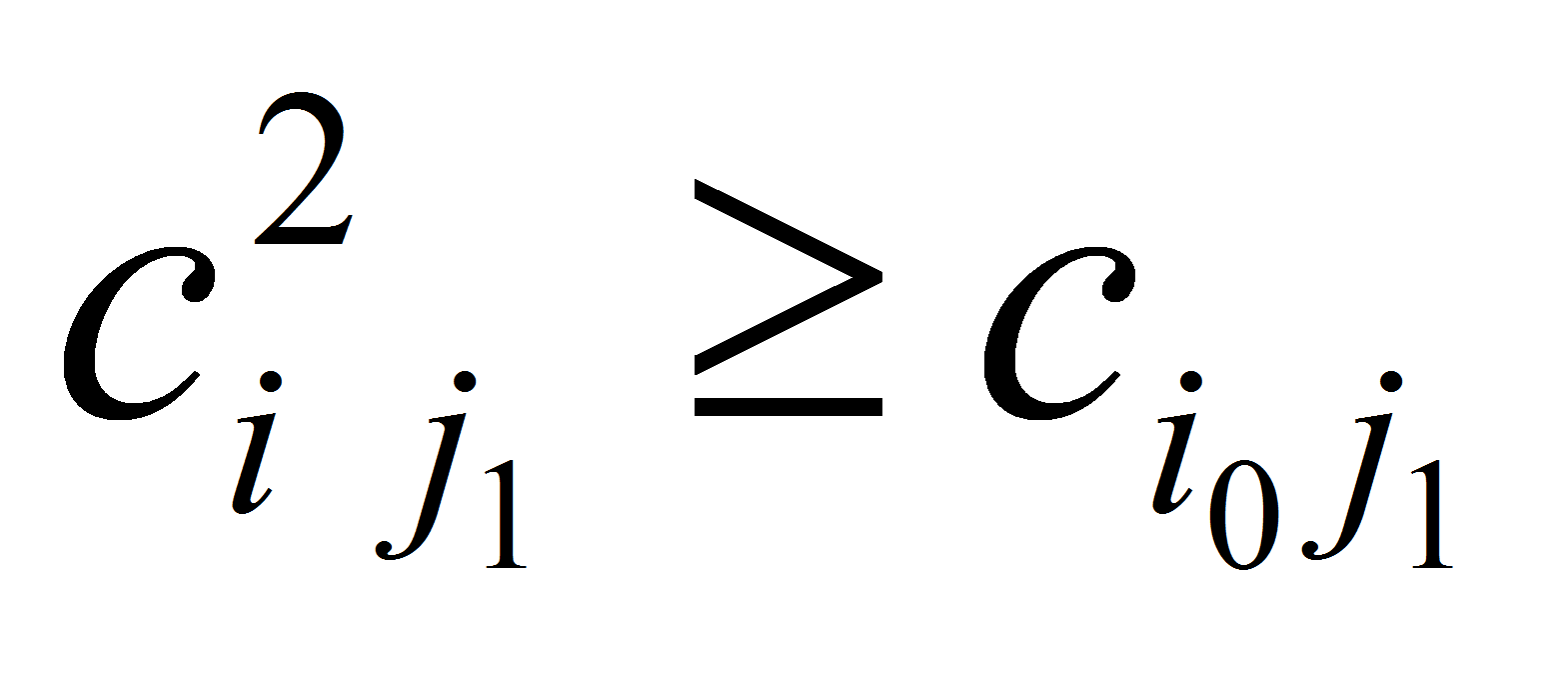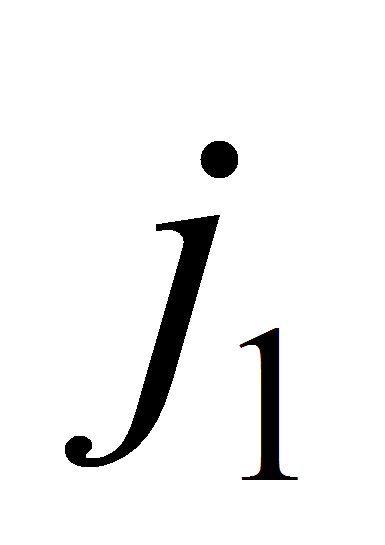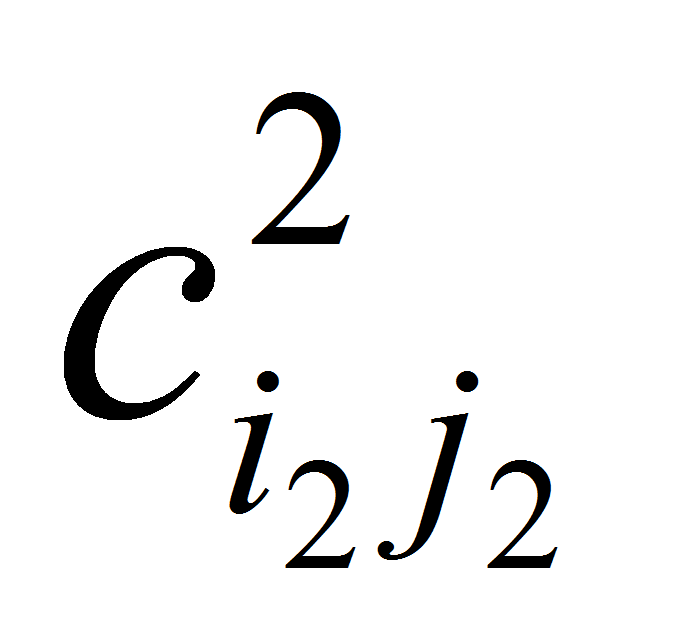
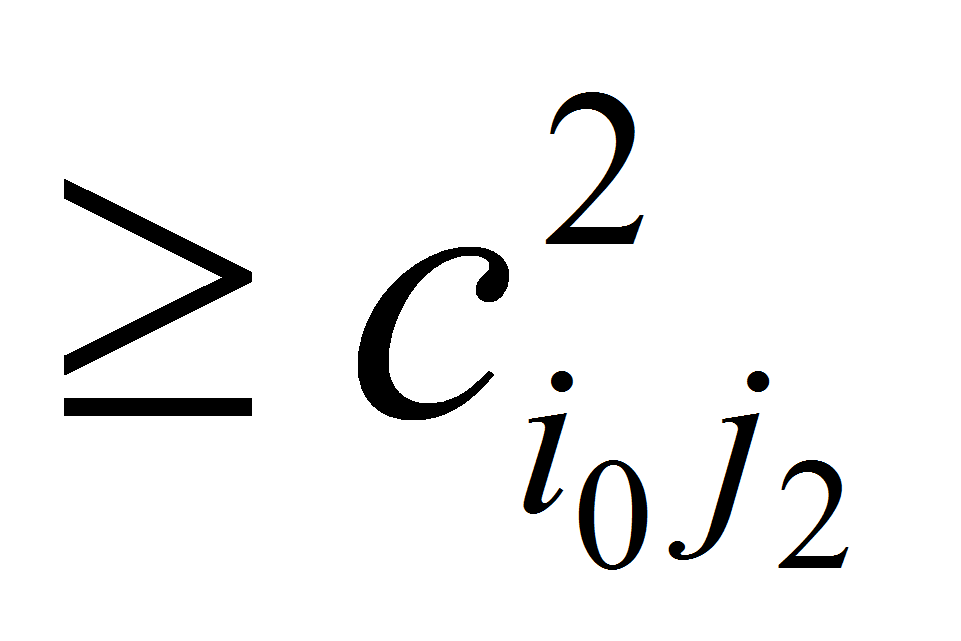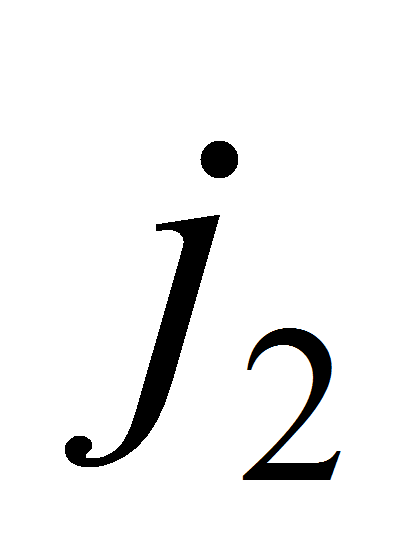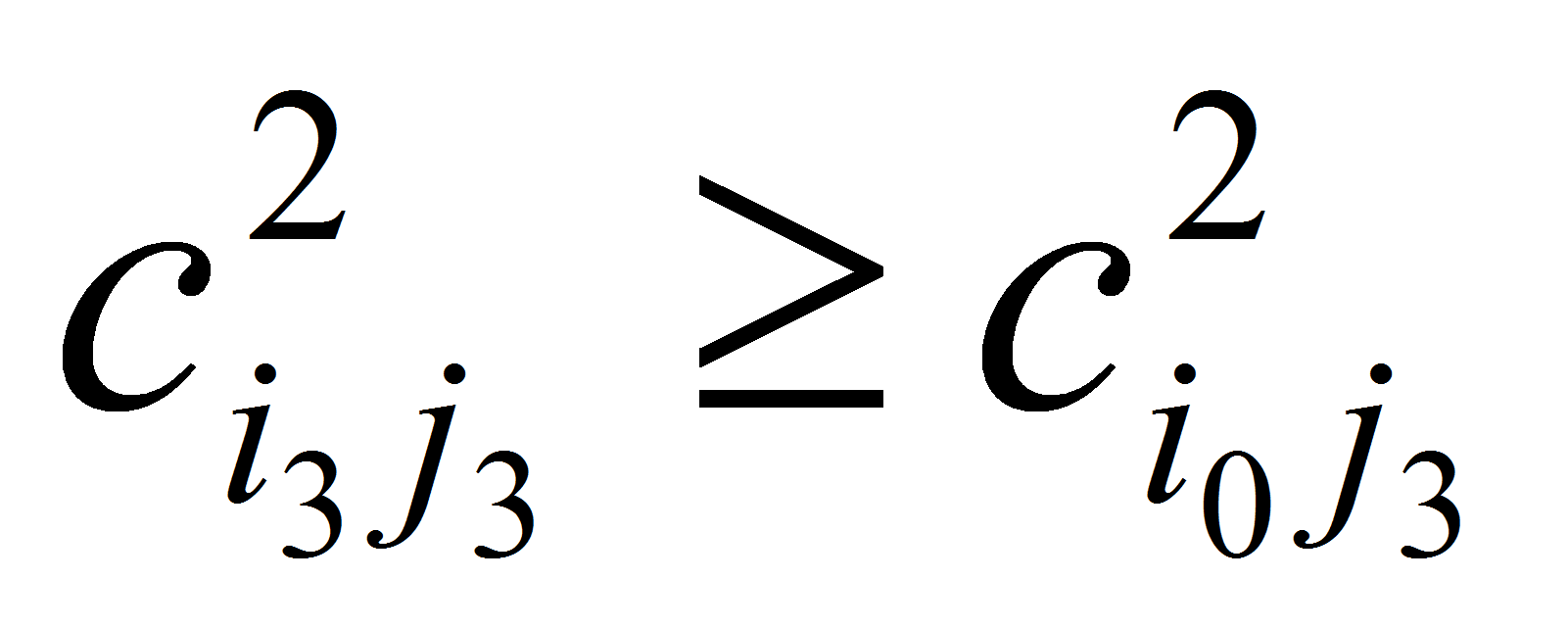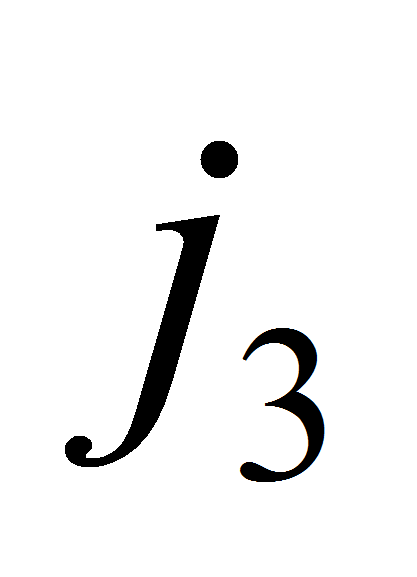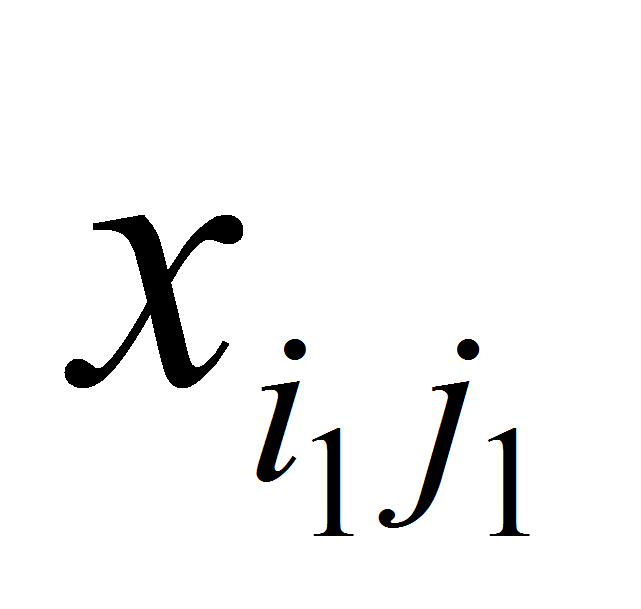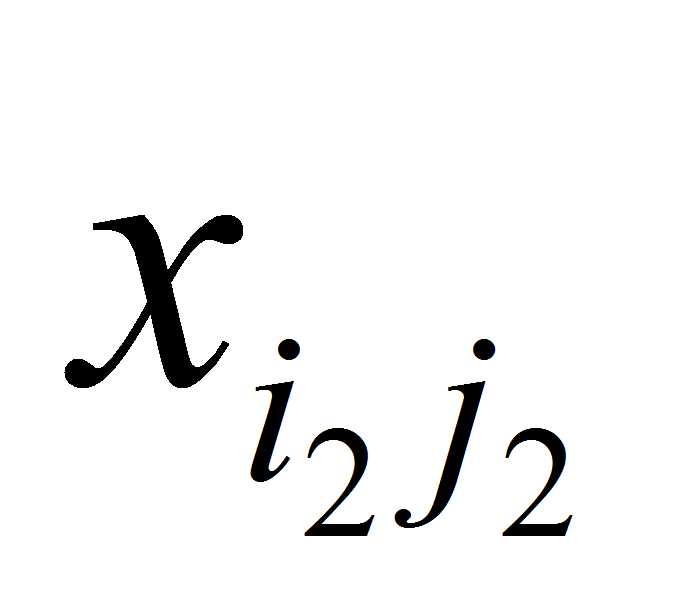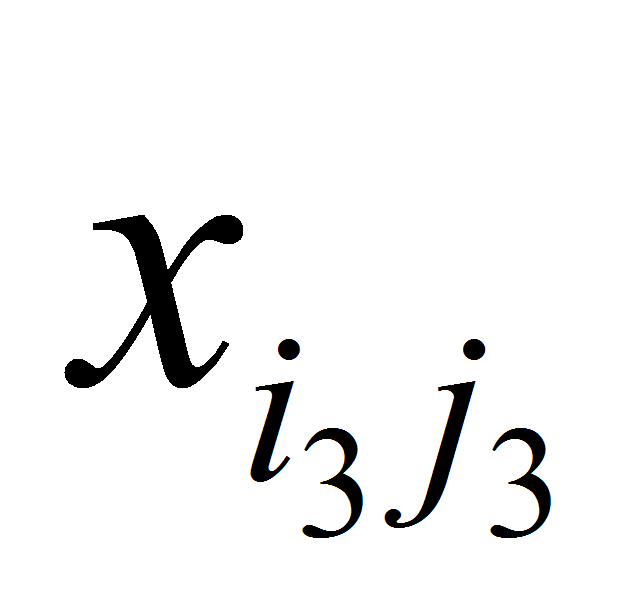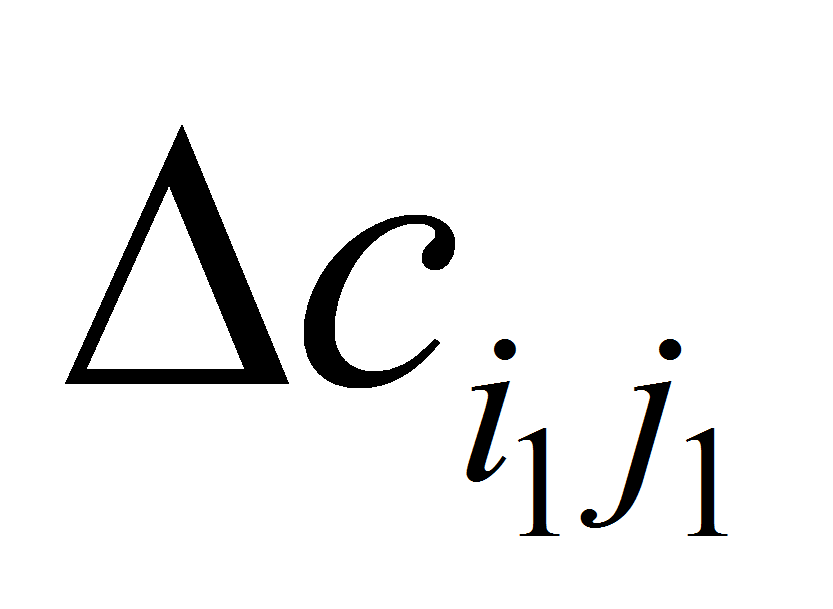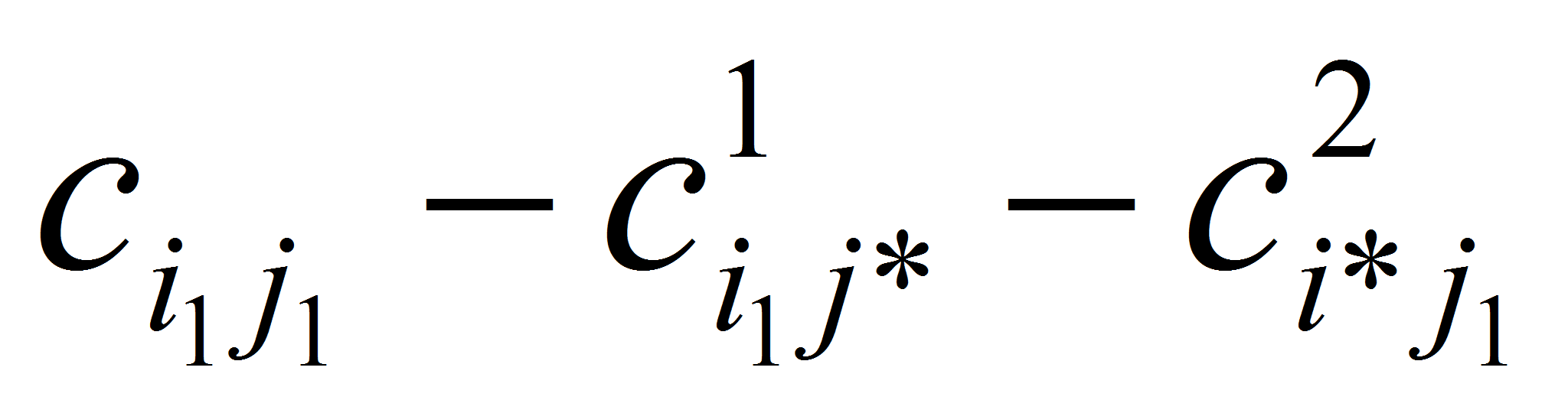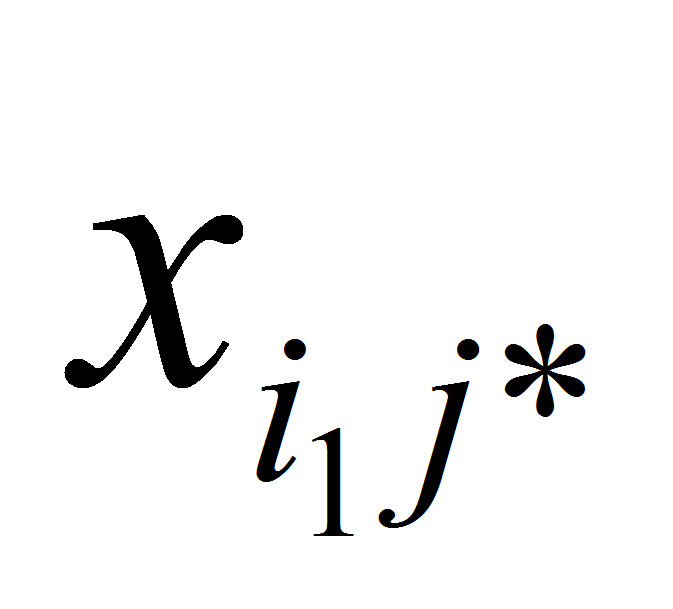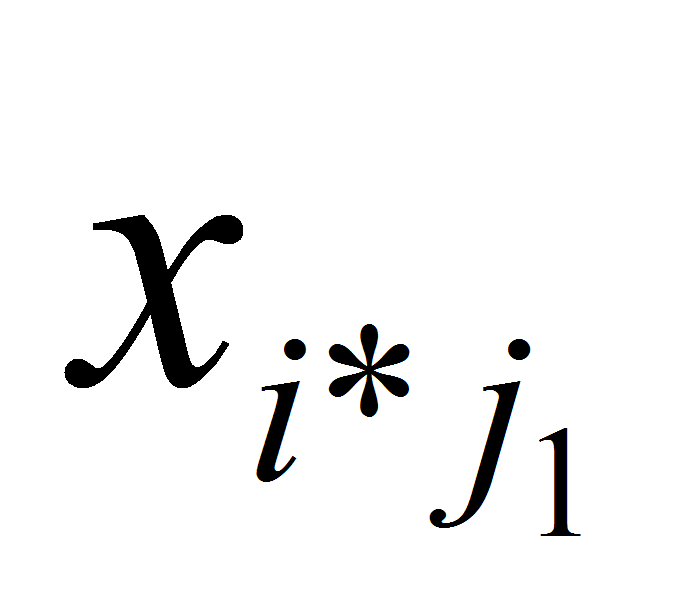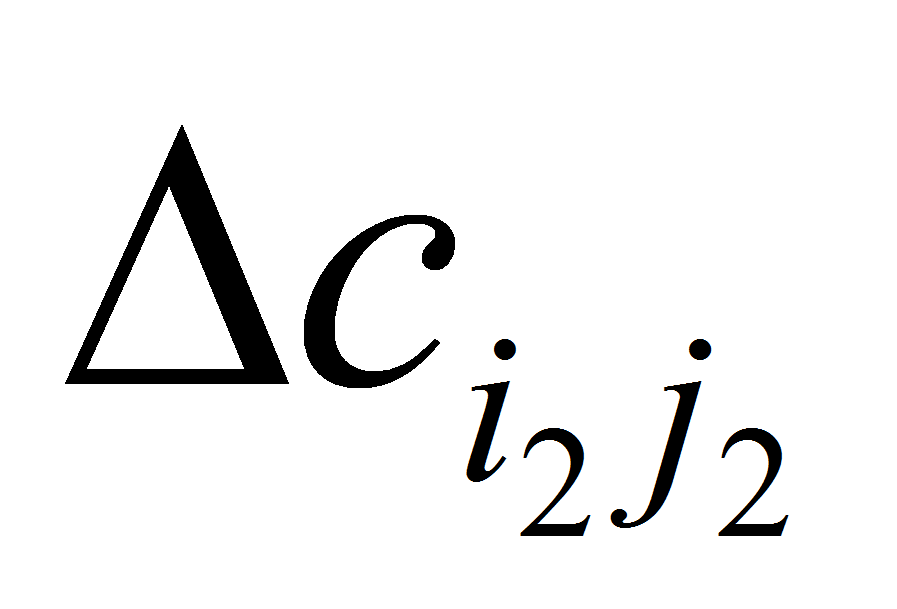Обозначим через = для в ограничении , а так же в ограничении и, наконец, в ограничении . При этом, очевидно. =0, =0, =0. Вычислим =, где и - переменные, попавшие в ограничения по итогам итерационного процесса (т.е. рассматриваемые на предмет присвоения им положительных значений), и по аналогии обозначим и .

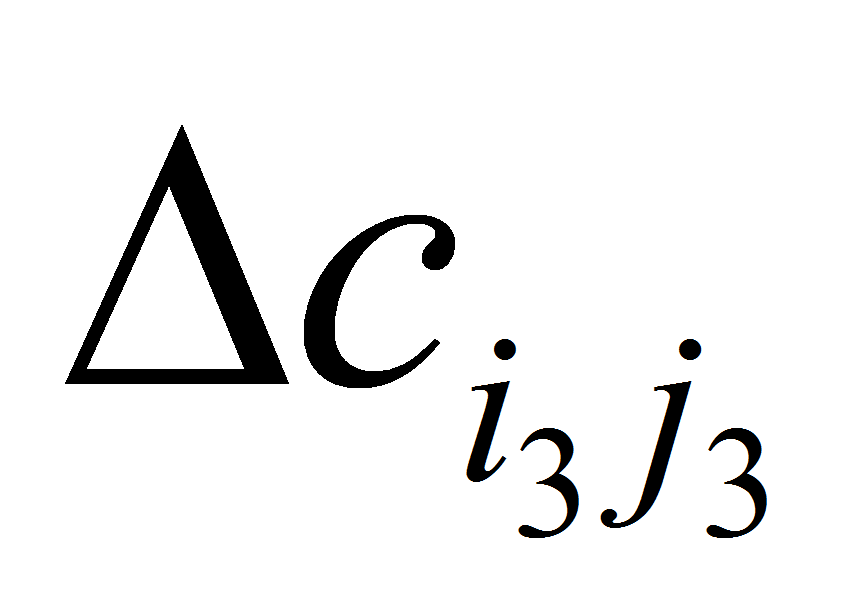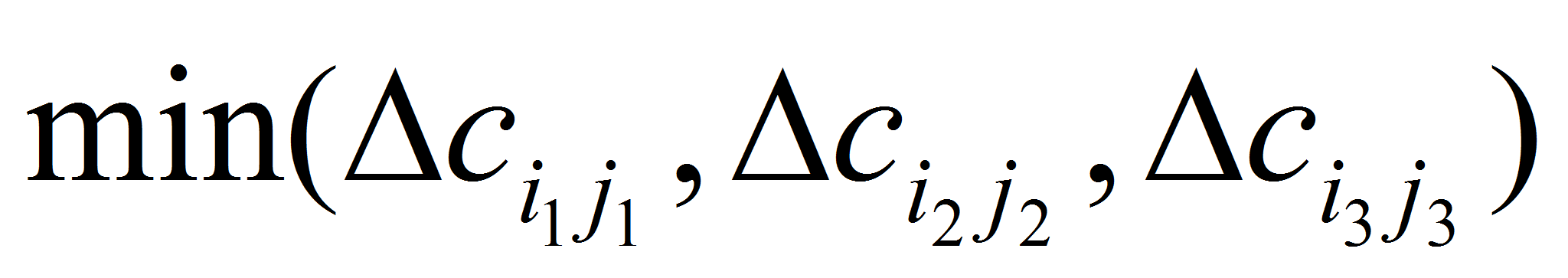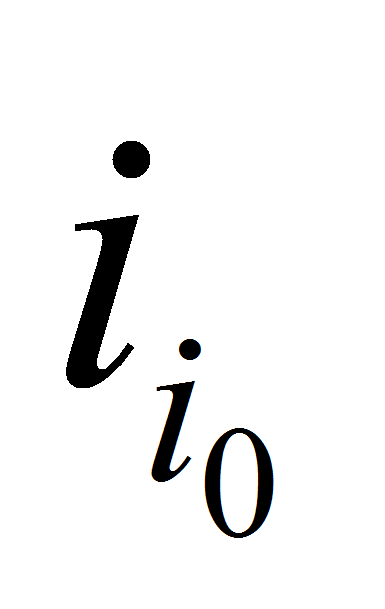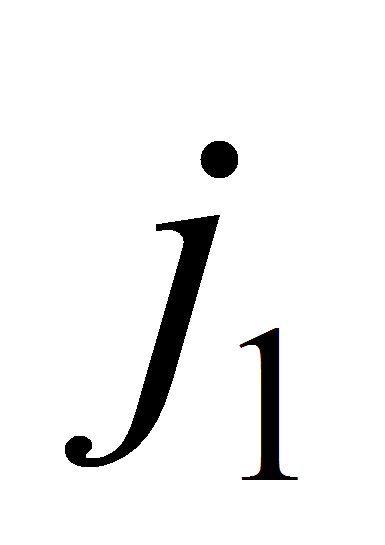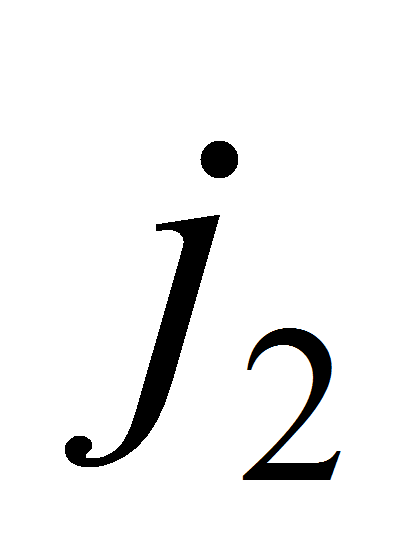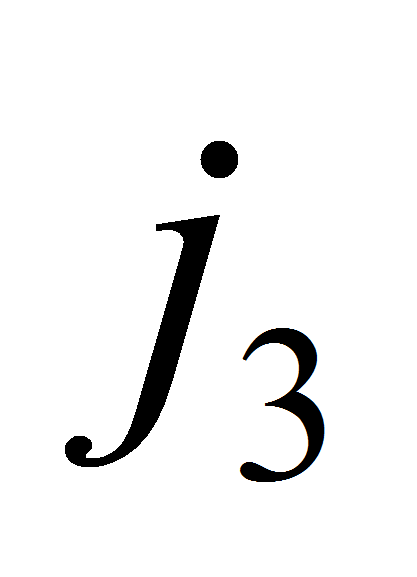Далее пусть =. Тогда очевидно, что, если, пользуясь утверждением Леммы, передать из целевой функции одномерной задачи (возможно увеличив её предварительно на достаточную величину) с номером ограничения величину в одномерные задачи с номерами , и соответственно, то, по крайней мере, в одной из пар задач с номерами ограничени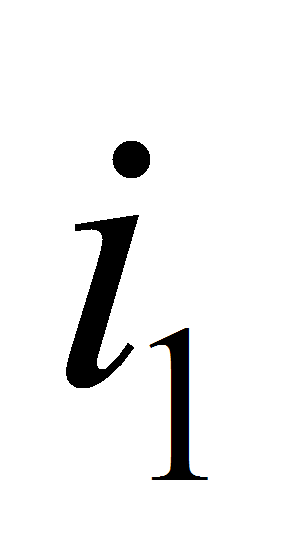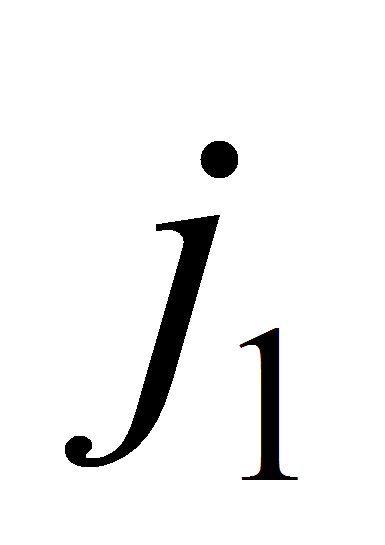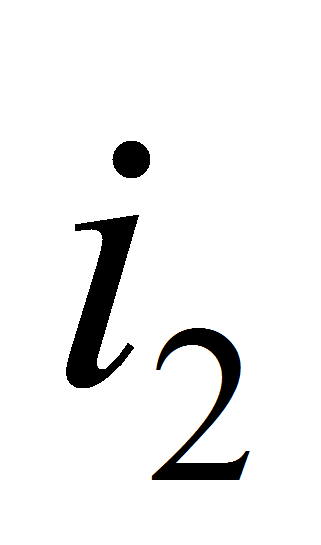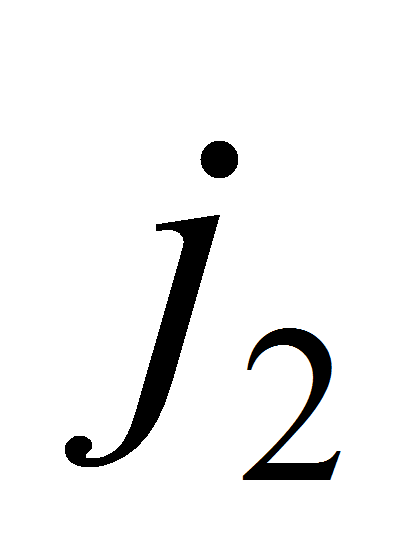й , (,или 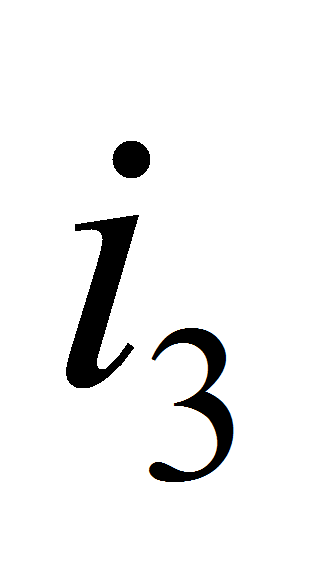,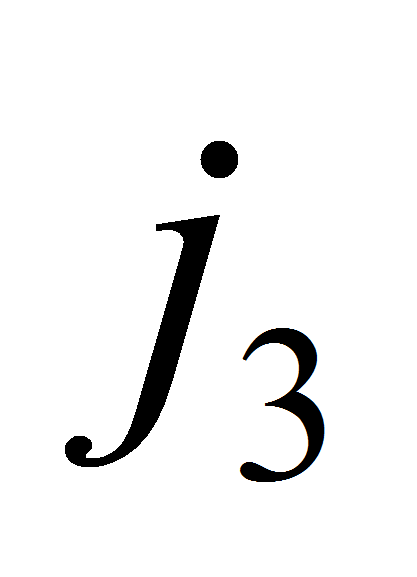) в ограничениях появится ещё одна переменная, которая может быть больше нуля, и тем самым неравенство (2.9) станет содержать больше переменных. 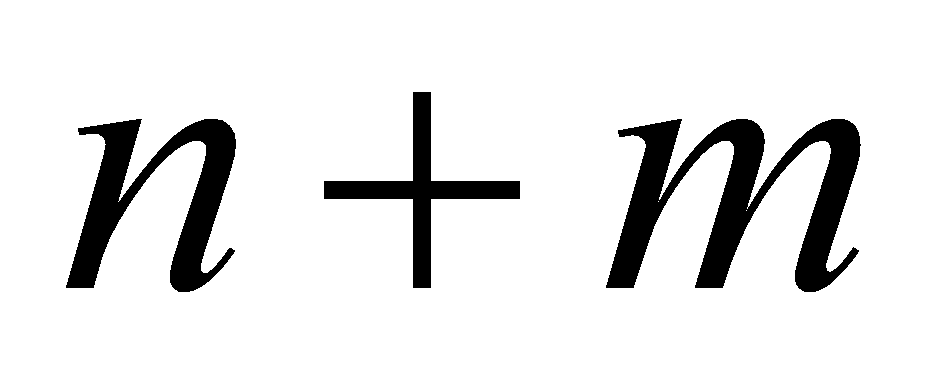После некоторого (заведомо меньшего, чем ) количества таких процедур будет получено оптимальное решение исходной транспортной задачи.

Литература:

1. Тизик А.П., Цурков В.И. Метод последовательных изменений параметров функционала в задаче о назначении // Автоматика и телемеханика. 2011. №12.

2. Гольштейн Е.Г., Юдин Д.Б. Задачи линейного программирования транспортного типа, М.: Наука, 1969 г.