Аффинный шифр Цезаря — это частный случай более общего моноалфавитного шифра подстановки. К шифрам подстановки относятся также шифр Цезаря, ROT13 и Атбаш [1].
Аффинный шифр Цезаря реализует простую подстановку, но обеспечивает немного большее пространство ключей по сравнению с шифром Цезаря. В аффинном шифре каждой букве алфавита размера m ставится в соответствие число из диапазона 0… m -1. Затем при помощи специальной формулы, вычисляется новое число, которое заменит старое в шифротексте.
Процесс шифрования можно описать следующей формулой (1):
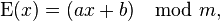
где x — номер шифруемой буквы в алфавите; m — размер алфавита; a, b — ключ шифрования.
Для расшифровки вычисляется другая формула (2):
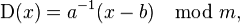
где a-1 — число обратное a по модулю m . Это значит, что для корректной расшифровки число a должно быть взаимно простым с m .
С учетом этого ограничения вычислим пространство ключей аффинного шифра на примере английского алфавита. Так как английский алфавит содержит 26 букв, то в качестве a может быть выбрано только взаимно простое с 26 число. Таких чисел всего двенадцать: 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23 и 25. Число b в свою очередь может принимать любое значение в интервале от 0 до 25, что в итоге дает нам 12*26 = 312 вариантов возможных ключей [2].
Обратный элемент по модулю. Часто в задачах требуется посчитать что-то по простому модулю (чаще всего). Это делают для того, чтобы участникам не приходилось использовать длинную арифметику, и они могли сосредоточиться на самой задаче. Обычные арифметические операции выполняются не сильно сложнее — просто нужно брать модули и заботиться о переполнении. Например:
c = (a + b) % mod;
c = (mod + a — b) % mod;
c = a * b % mod;
Но вот с делением возникают проблемы — мы не можем просто взять и поделить. Пример (3):
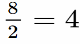
Но (4)
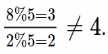
Нужно найти некоторый элемент, который будет себя вести как, и вместо «деления» домножать на него (5).
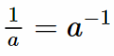
Назовем такой элемент обратным [4].
Разработка программы
Реализация алгоритма
Процесс шифрования
- Создаем цикл с параметром, в который будет выполнятся от 0 до длины строки с шагом 1.
- Берем 1 элемент из строки и записываем его представление в таблице ASCII в переменную E .
- Разделяем на строчные и заглавные символы латиницы и выполняем шифрование по формуле (1).
- Переводим полученный дешифрованный символ в по таблице ASCII и объединяем заменяем им место исходного символа.
Процесс дешифрования
- Создаем цикл с условием для нахождения обратного элемента по модулю и присваиваем полученное значение переменной A .
- Создаем цикл с параметром в который будет выполнятся от 0 до длины строки с шагом 1.
- Берем 1 элемент из строки и записываем его представление в таблице ASCII в переменную D .
- Разделяем на строчные и заглавные символы латиницы и выполняем шифрование по формуле (2) и дополнительно к получившимся отрицательным значениям символов прибавляем 26 чтобы значения символов алфавита находились в пределе от 0 до 26.
- Переводим полученный дешифрованный символ в по таблице ASCII и объединяем заменяем им место исходного символа.
Процесс дешифрования показан в полном листинге программы
Листинг программы:
#include
#include
using namespace std;
void main()
{ char t;
string text;
int i, size, E, D, A, B, X, Op;
cout << "Enter text:" << endl;
getline(cin, text);// Считывание текста до первого символа
size = text.length(); // Длина строки
// Переменная A не может быть четным или быть равно 13
cout << "Enter A and B:" << endl;
cout << "(A must not be even or equal to 13)" << endl;
cin >> A >> B;
cout << "1) Encrypting\n2) Decrypting" << endl;
cin >> Op;
// Шифрование
if (Op == 1) {
for (i = 0; i < size; i++) {
t = text[i];// Взятие одного символа из строки
E = (int)(t);// Представление символа в коде ASCII
if (((int)(t) >= 97) && ((int)(t) <= 122)) {
X = (int)(t)-97;
E = ((A * X + B) % 26) + 97;}
if (((int)(t) >= 65) && ((int)(t) <= 90)) {
X = (int)(t)-65;
E = ((A * X + B) % 26) + 65;}
t = (char)(E);
text[i] = t;
}
}
if (Op == 2) {
i = 1;
while ((A * i) % 26 != 1) { i++; }
A = i;
for (i = 0; i < size; i++) {
t = text[i];
D = (int)(t);
if (B > 26) { B = B % 26; }
if (((int)(t) >= 97) && ((int)(t) <= 122)) {
X = (int)(t)-97;
D = (A * (X - B)) % 26;
if (D < 0) { D = D + 26; }
D = D + 97;
}
if (((int)(t) >= 65) && ((int)(t) <= 90)) {
X = (int)(t)-65;
D = (A * (X - B)) % 26;
if (D < 0) { D = D + 26; }
D = D + 65;
}
t = (char)(D);
text[i] = t;
}
}
cout << "Result:" << endl;
cout << text << endl;
system("pause");
}
Тестирование
Из первого теста (рисунок) мы узнаём, что компьютер получил от пользователя строку с текстом, A и B. Далее, перед пользователем встаёт выбор, и после того на экран выводится результат.
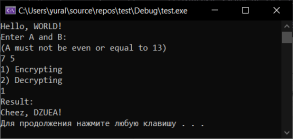
Рис. 1. Тест № 1
Проверим работоспособность программы при дешифровке полученного от нее сообщения (рисунок 2).
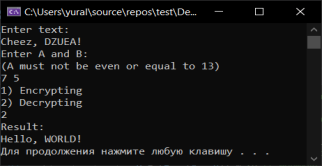
Рис. 2. Тест № 2
Тест № 2 (рисунок 2) подтверждает работоспособность программы. Результат выводится пользователю в консоли. Ошибок при компиляции и при выполнении программы обнаружены не были.
Литература:
- А. Л. Фридман — «Язык программирования C++» [текст]
- Л. Г. Гагарина, В. Д. Колдаев –«Алгоритмы и структуры данных» [текст]
- Б. Пахомов — «C/C++ и Microsoft Visual C++» [текст]
- А. Побегайло — «C/C++ для студента: производственно-практическое издание» [текст]
- А. Мешков, Ю. Тихомиров — «Visual C++ и MFC» — М.: БХВ-Петербург, 2013. [текст]
- Роберт С. Сикорд — Безопасное программирование на C и C++ — Москва: РГГУ, 2014. [текст]

