Впервые построением и изучением свойств оператора , являющегося обращением оператора свертки с функцией , занимался С. Л. Соболев. Для описание некоторого аналитического алгоритма отыскания оптимальных коэффициентов С. Л. Соболев определил и исследовал дискретный аналог полигармонического оператора . Задача построения дискретного оператора при произвольном оказалось очень трудной.

В одномерном случае, т. е. дискретный аналог оператора построен З. Ж. Жамоловым [2]. Но там вид этой функции выписан с точностью до - неизвестного коэффициента. В работе Шадиметова [3] найдены эти коэффициенты, тем самым дискретный аналог оператора полностью построен. Построением дискретного аналога дифференциального оператора и занимались Шадиметов Х. М., Хаетов А. Р. [4,5].

Настоящая работа является продолжением работы [6].

В этой работе дан алгоритм построение оператора , которая удовлетворяет равенству

. (1)

Здесь . (2)

Основным результатом является следующая

Теорема. Оператор удовлетворяющий равенству (1)

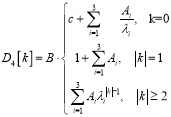(3)

определяется формулой где

,

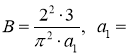
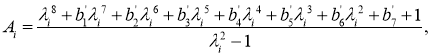
, (5)

, здесь

— корни многочлена =,

, здесь

,

,

.

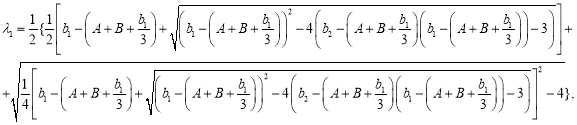
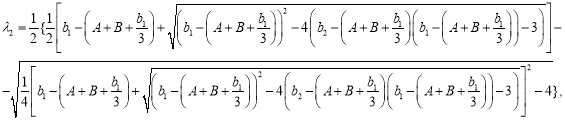
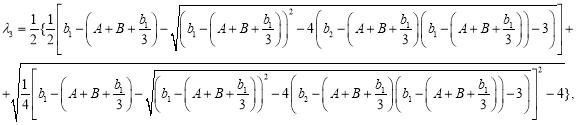
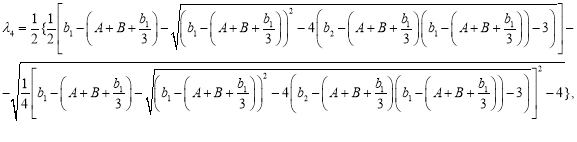
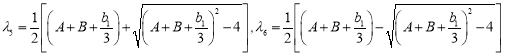Где

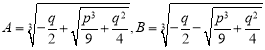, здесь

, и — малый параметр.

Литература:

1. Соболев С. Л. Введение в теорию кубатурных формул. М.: Наука 1974. — 808 с.
2. Жамолов З. Ж. Об одном разностном аналоге оператора 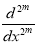и его построение.
3. В кн.: Прямые и обратные задачи для дифференциальных уравнений с частными производными и их приложения. Ташкент. Фан, 1978, -с. 97–108.
4. Шадиметов Х. М. Дискретный аналог дифференциального оператора 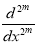и его построение. Вопросы вычислительной и прикладной математики. — Ташкент, 1985, -с. 22–25.
5. Шадиметов Х. М., Хаетов А. Р. Построение дискретного аналога дифференциального оператора 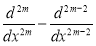УзМЖ, 2004, № 2, -с. 85–95.
6. Хаетов А. Р. Построение дискретного аналога дифференциального оператора 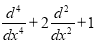и его свойства. УзМЖ, 2009, № 3, -с. 81–88.
7. Жалолов Ик.И. Алгоритм построения дискретного аналога 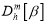одного оператора. Проблемы вычислительной и прикладной математики. Ташкент, 2015, № 2, -с. 48–52.