В этой работе мы рассмотрим алгоритм координации для системы, в которой модели элементов задаются дифференциальными уравнениями.
Приведенный алгоритм, основанный на теории двойственности, является одним из простейших алгоритмов координации в динамических системах. Более сложные и совершенные алгоритмы приведены в работе [2].
Пусть система состоит из N взаимосвязанных подсистем, каждая из которых описывается системой линейных дифференциальных уравнений:
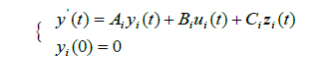(1)
Здесь 
вектор выходов 
го элемента, 
-вектор уравнений 
- го элемента, 
вектор входов го элемента, 
матрицы с постоянными коэффициентами.
Предполагается, что вектор входов 
является линейной комбинацией выходов других подсистем:
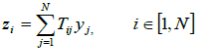(2)
Заметим, что в (2) не исключается возможность того, что 
, т.е не исключаем возможности обратной связи в подсистемах.
Если уравнения взаимосвязи 
подставить в (1), то можно получить стандартную форму
(3)
Где А и В — полные матрицы системы.
Глобальная целевая функция имеет вид
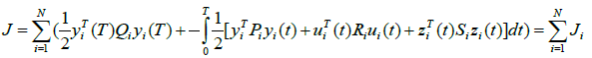(4)
Где 
положительно определенные матрицы, 
строго положительно определенные матрицы, 
локальная целевая функция го элемента:
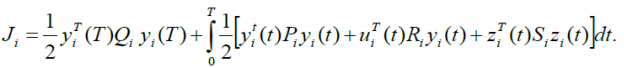
Член 
под интегралом в (4) вводится для того, чтобы исключить вырожденные случаи.
Рассмотрим приведенный в (2) алгоритм, осуществляющий двухуровневую процедуру решения задачи. Алгоритм основан на модификации целей элементов путем введения штрафов за невыполнение ограничений (2).
Введем двойственную функцию 
при соблюдении ограничений (1); где L- лагранжиан, определяемый формулой
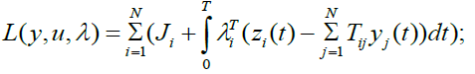
вектор множителей Лагранжа.
Для заданного значения вектора множителей Лагранжа
лагранжиан можно записать в виде
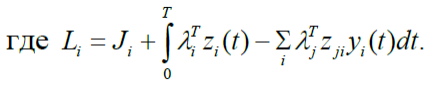
Таким образом, для заданного 
= 
оказывается возможным максимизировать подлагранжианы 
независимо для каждого элемента. Поэтому значение двойственного функционала 
определяется путем независимого решения N локальных задач вида
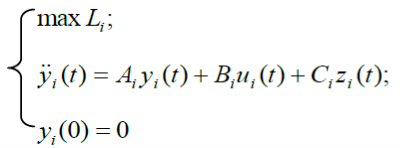
Известно [2], что для рассматриваемой задачи выполняется равенство
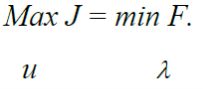
Таким образом, задача сводится к минимизации двойственного функционала по . Это можно осуществить в соответствии с двухуровневой структурой, когда на нижнем уровне при фиксированном значении решаются независимо N локальных задач а на верхнем уровне решается задача выбора оптимального значения вектора .
Механизм последовательного улучшения значений функции F() основан на том факте, что оказывается возможным вычислить простое выражение для градиента F() в терминах решений, получаемых при решении задач локальной максимизации.
Градиент задается ошибкой между прогнозным и фактическим значением входов подсистем, т. е.
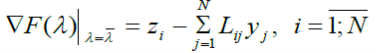
Этот вектор ошибок используется в градиентной процедуре для формирования нового значения вектора .
Последовательное изменение вектора происходит по формулам
где к означает номер итерации; 
длина шага; 
направление.
Если используется метод наискорейшего спуска, то 
; если используется метод сопряженных градиентов то
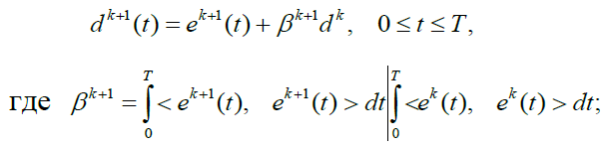
Процедура заканчивается, когда 
,
достаточно близко к нулю.
Литература:
- Алиев Р.А, Либерзон М. Н. Об одном подходе к координации в двухуровневых нечетких системах. Рига: Риж. политех. Ин-т.1983.
- Singh M. G. Dynamical Hierarchical Contol -Amsterdam North-Holland, 1977.-
