В современном мире финансов и инвестиций, где неопределенность и риск играют ключевую роль, использование передовых методов анализа становится необходимостью для успешного формирования инвестиционных портфелей. Одним из таких методов, привлекающих все большее внимание и признание, является применение нечетких множеств. Нечеткие множества предоставляют инвесторам инструмент для более гибкого и адаптивного подхода к принятию решений, учитывая разнообразные факторы, влияющие на финансовые рынки. В данной статье мы рассмотрим ключевые аспекты использования нечетких множеств в формировании инвестиционного портфеля, их преимущества и потенциальные вызовы, а также примеры успешного применения этого подхода в условиях современной инвестиционной среды.
В классических моделях при формировании инвестиционного портфеля принято ориентироваться на показатели риска и доходности активов, но наряду с ними есть показатели, которые могут повлиять на выбор инвестора. Примером могут являться показатели финансовой устойчивости организации, отраженные в таблице 1.
Таблица 1
Показатели финансовой устойчивости
|
Показатель |
Описание |
Нормативные пределы |
|
Коэффициент автономии |
Доля активов, обеспеченных собственными ресурсами |
0,5–0,7 |
|
Коэффициент финансового левериджа |
Отношение заемных средств к собственным |
0,43–1 |
|
Коэффициент обеспеченности собственными оборотными средствами |
Обеспеченность собственными средствами для поддержания текущей деятельности |
> 0,1 |
|
Коэффициент покрытия инвестиций |
Доля активов, финансируемых за счет собственных средств и долгосрочных кредитов |
> 0,65 |
|
Коэффициент обеспеченности запасов |
Степень обеспеченности запасов собственными средствами |
≥ 0,5 |
|
Коэффициент краткосрочной задолженности |
Доля краткосрочных обязательств среди общих обязательств |
0–0,5 |
Нормы коэффициентов имеют различный диапазон, к тому же для сравнения необходимо добавить доходность и риск, измеряющиеся в процентах. Для того, чтобы привести все показатели в одну систему измерения необходимо воспользоваться методом нечетких множеств.
Необходимо ввести переменную M, которая будет означать оценку выбранной акции для формируемого портфеля, имеющую множество значений {M 1 ; M 2 ; M 3 ; M 4 ; M 5 }, расположенных на отрезке [0;1]. Значение M 1 будет соответствовать оценке «5», M 2 — оценке «4», M 3 — оценке «3», M 4 — оценке «2», M 5 — оценке «1» [1, с.10]. Для формирования оценки введем терм-подмножество m, расположенное так же в диапазоне [0;1]. В таблице 2 указаны функции принадлежности терм-подмножеств m терму M.
Таблица 2
Функции принадлежности терм-подмножеств m [1]
|
Терм M k |
Функция принадлежности |
|
M5 ≡ [0;0,25] |
μ5 = 1, если 0≤m≤0,15; 10(0,25-m), если 0,15 |
|
M4 ≡ (0,15;0,45] |
μ4 = 1–10(0,25-m), если 0,15 <m≤0,45; <="" p=""> </m≤0,45;> 1, если 0,25 <m≤0,55; <="" p=""> </m≤0,55;> 10(0,45-m), если 0,35 <m≤0,45 <="" p=""> </m≤0,45> |
|
M3 ≡ (0,35;0,65] |
μ3 = 1–10(0,45-m), если 0,35 <m≤0,65 <="" p=""> </m≤0,65> 1, если 0,45 <m≤0,55; <="" p=""> </m≤0,55;> 10(0,65-m), если 0,55 <m≤0,65 <="" p=""> </m≤0,65> |
|
M2 ≡ (0,55;0,85] |
μ2 = 1–10(0,65-m), если 0,55 <m≤0,65; <="" p=""> </m≤0,65;> 1, если 0,65 <m≤0,75; <="" p=""> </m≤0,75;> 10(0,85-m), если 0,75 <m≤0,85 <="" p=""> </m≤0,85> |
|
M1 ≡ [0,75;0,1] |
μ1 = 1–10(0,85-m), если 0,75≤m≤0,85; ≤m≤0,85; 1, если 0,85≤m≤1 |
Значение m рассчитывается как удельный вес экспертных оценок. В данном случае экспертные оценки строятся на основе показателей финансовой устойчивости, доходности и риска и имеют собственные характеристики A ij , где A i 1 — крайне низкий уровень показателя, A i 2 — низкий уровень; A i 3 средний уровень, A i 4 — высокий уровень, A 5 — очень высокий уровень.
Таблица 3
Экспертные оценки [ 1, с.18 ]
|
Показатель |
Терм | ||||
|
A i1 |
A i2 |
A i3 |
A i4 |
A i5 | |
|
Коэффициент автономии |
(a 1 ;a 2 ;a 3 ;a 4 ) |
(a 3 ;a 4 ;a 5 ;a 6 ) |
(a 5 ;a 6 ;a 7 ;a 8 ) |
(a 7 ;a 8 ;a 9 ;a 10 ) |
(a 9 ;a 10 ;a 11 ;a 12 ) |
|
Коэффициент финансового левериджа |
(a1;a2;a3;a4) |
(a3;a4;a5;a6) |
(a5;a6;a7;a8) |
(a7;a8;a9;a10) |
(a9;a10;a11;a12) |
|
Коэффициент обеспеченности собственными оборотными средствами |
(a1;a2;a3;a4) |
(a3;a4;a5;a6) |
(a5;a6;a7;a8) |
(a7;a8;a9;a10) |
(a9;a10;a11;a12) |
|
Коэффициент покрытия инвестиций |
(a1;a2;a3;a4) |
(a3;a4;a5;a6) |
(a5;a6;a7;a8) |
(a7;a8;a9;a10) |
(a9;a10;a11;a12) |
|
Коэффициент обеспеченности запасов |
(a1;a2;a3;a4) |
(a3;a4;a5;a6) |
(a5;a6;a7;a8) |
(a7;a8;a9;a10) |
(a9;a10;a11;a12) |
|
Коэффициент краткосрочной задолженности |
(a1;a2;a3;a4) |
(a3;a4;a5;a6) |
(a5;a6;a7;a8) |
(a7;a8;a9;a10) |
(a9;a10;a11;a12) |
Пределы a ij определяются в зависимости от уровня показателя, например, если коэффициент имеет среднее значение 0,5, то минимальный уровень A i 1 будет находиться в пределах [0;0;0,25;35]. Для каждого коэффициента эти пределы будут индивидуальны и зависимы от того, как их определит эксперт.
Исходя из того, между каких a ij находится значение исследуемого показателя ему присваивается оценка, как указано на рисунке 1.
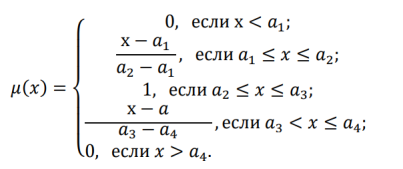
Рис. 1. Принадлежность показателя множеству экспертных оценок
После получения оценок рассчитывается удельный вес оценок по всем показателям. Если заранее известна степень важности показателей, то вес определяется по правилу Фишберна:
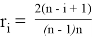
где n — количество показателей;
i — порядковый номер показателя.
Значение m затем вычисляется по формуле:
m =
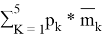
В итоге получится значение m, по которому можно будет определить оценку актива, отражающую в себе не только показатели доходности и риска, но и другие возможные характеристики, необходимые для инвестора.
Метод нечетких множеств позволяет привести в единую систему разнородные по своей сути показатели, произвести анализ и на его основе принять эффективное решение о необходимости включения в портфель акции или же исключения ее.
Литература:
- Недосекин А. О. Применение теории нечетких множеств к задачам управления финансами / А. О. Недосекин // Аудит и финансовый анализ. –2000. — № 2.

