В постановке задачи для решения ее с помощью математического аппарата марковских цепей, системный аналитик и лицо, принимающее решения, предстают перед необходимостью работы с четкой и жесткой системой, в которой необходимо все разделить строго на истину и ложь, чтобы соблюдались условия не пересечения событий и наличия полной группы событий, хотя в реальных экономических процессах строгое разделение событий может оказаться затруднительным. Таким образом, отнесение пограничных состояний к какому-либо одному жестко заданному состоянию может привести к искажению результата и, соответственно, снизить качество принимаемых решений.
В данной работе проведено исследование возможности применения нечеткой логики в принятии управленческих решений на примере обобщения классической «четкой» теории марковских цепей с помощью аппарата нечетких множеств.
В рамках традиционной «четкой» теории случайных процессов Маркова построена модель управления стимулированием покупателей дистрибьюторского центра (ДЦ). В модели управления степень стимулирования выражается через процент предоставленных той или иной группе покупателей скидок.
Всех покупателей ДЦ можно разделить на 3 группы: оптовые покупатели, розничные покупатели и ключевые клиенты. Cостав (и, соответственно, размер) групп может измениться как следствие применения той или иной стратегии управления. Следовательно, имеется четыре состояния системы управления стимулированием покупателей ДЦ:
S1: Отсутствие стимулирования отдельной группы покупателей.
S2: Стимулирование оптовых покупателей.
S3: Стимулирование розничных покупателей.
S4: Стимулирование ключевых клиентов.
Решение о выборе стратегии принимается на основе текущей конъюнктуры деловой среды, состоящей из различных постоянно меняющихся факторов, таких, как уровень спроса, налоговое законодательство, государственное регулирование рынка и т. д. Таким образом, вероятность перехода системы из состояния Si в состояние Sj зависит только от i и j и не зависит от поведения системы до момента ее попадания в состояние Si. Поскольку далее мы будем рассматривать систему, переходящую из одного состояния в другое через определенные промежутки времени, то описанный процесс является дискретным марковским процессом с дискретным временем.
Для оценки результатов функционирования системы при применении той или иной стратегии нам необходимо знать вектор финальных вероятностей. Процедура поиска этого вектора хорошо известна [1].
Для оценки влияния выбора стратегии на экономические показатели работы ДЦ, определим цены состояний, которые наиболее полно будут отражать экономические аспекты работы ДЦ с покупателями:
Объем продаж — сумма отгруженных товаров с учетом скидок в денежном выражении (положительный показатель).
Скорость оплаты — сумма оплаченных клиентами счетов из расчета за 1 день, т. е. сумма оплаты, деленная на количество дней с момента отгрузки до момента оплаты (положительный показатель).
Сумма предоставленных скидок — сумма скидок в денежном выражении (отрицательный показатель). Под нормированной долей скидок, предоставленных той или иной группе покупателей, понимается доля скидок, предоставленных этой группе относительно суммы процентов скидок, предоставленных всем группам покупателей.
Таким образом, мы можем уточнить определение состояний следующим образом: если нормированная доля скидок, предоставленных каждой группе, меньше или равна 50 %, то имеет место состояние S1; если доля скидок, предоставленных группе оптовых покупателей, больше 50 %, то имеет место состояние S2; если доля скидок, предоставленных группе розничных покупателей, больше 50 %, то имеет место состояние S3; если доля скидок, предоставленных группе ключевых клиентов, больше 50 %, то имеет место состояние S4.
Разделение состояний по принципу «более 50 %» хотя и позволяет строго задать условия марковского процесса, но противоречит человеческой интуиции. Действительно, если, например, оптовые покупатели получили за какой-то период времени 51 % от общей суммы скидок, а розничные 49 %, то в этом случае система окажется в состоянии S2, хотя очевидно, что это некоторое пограничное состояние между S2 и S3. Таким образом, правильней было бы определить состояния системы на основе теории нечетких множеств, введенной Л. Заде [2]. Для этого введем лингвистическую переменную «Нормированный процент скидки», которая определяется следующими параметрами:
Универсальное множество U — множество действительных чисел в диапазоне [0, 100].
Ограничение R1 — «Маленький».
Ограничение R2 — «Большой».
Функцию принадлежности mR(u), где u — элемент универсального множества U, определим следующим образом:
mм(U) = 1, где 0 £ x < 25
mм(U) = -0.02x + 1.5, где 25 £ x £ 75
mм(U) = 0, где 75 < x £ 100
mб(U) = 0, где 0 £ x < 25
mб(U) = 0.02x — 0.5, где 25 £ x £ 75
mб(U) = 1, где 75 < x £ 100
где x — нормированный процент скидки
mм(U) — функция принадлежности нормированных процентов скидок ограничению R1.
mб(U) — функция принадлежности нормированных процентов скидок ограничению R2.
Тогда мы можем определить состояния системы следующим образом:
S1: Все группы получают «небольшой» нормированный процент скидки
S2: Группа оптовых покупателей получает «большой» нормированный процент скидки
S3: Группа розничных покупателей получает «большой» нормированный процент скидки
S4: Ключевые клиенты получают «большой» нормированный процент скидки
Таким образом, мы получили 4 нечетких состояния, поскольку, например, если, оптовые покупатели получили за какой-то период времени 51 % от общей суммы скидок, а розничные 49 %, то в этом случае система одновременно будет находиться в состояниях S2 и S3, но с разными степенями уверенности.
Для дальнейших операций определим более строго лингвистическую переменную «Система», значением которой может быть одно из приведенных выше нечетких состояний:
Универсальное множество U — полная группа состояний системы.
Ограничение Ri — Состояние Si, i = 1..4.
Степень принадлежности системы состояниям mR(u), где u — элемент универсального множества U; R — одно из состояний.
Систему будем обозначать символом S без индексов.
Для определения того, в каком состоянии и с какой степенью уверенности mR(u) находится система в тот или иной момент времени, введем 4 правила нечеткого вывода:
1. Если все группы получили небольшой нормированный процент скидки, то имеет место состояние S1.
2. Если группа оптовых покупателей получила большой нормированный процент скидки, а все остальные небольшой, то имеет место состояние S2.
3. Если группа розничных покупателей получила большой нормированный процент скидки, а все остальные небольшой, то имеет место состояние S3.
4. Если группа ключевых клиентов получила большой нормированный процент скидки, а все остальные небольшой, то имеет место состояние S4.
Для расчета матрицы вероятностей переходов между нечеткими состояниями введем нечеткое событие 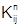 , заключающееся в том, что система на n-ом шаге была в состоянии Si, а на (n+1)-м шаге оказалась в состоянии Sj. Следовательно, для определения степени уверенности в том, что событие
, заключающееся в том, что система на n-ом шаге была в состоянии Si, а на (n+1)-м шаге оказалась в состоянии Sj. Следовательно, для определения степени уверенности в том, что событие 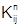 произошло, можно воспользоваться правилом нечеткого вывода:
произошло, можно воспользоваться правилом нечеткого вывода:
ЕСЛИ на n-ом шаге система находится в состоянии 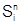 И на (n+1)-м шаге система находится в состоянии
И на (n+1)-м шаге система находится в состоянии 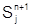 ТО произошло событие
ТО произошло событие 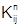 .
.
Тогда матрицу вероятностей переходов между нечеткими состояниями мы можем рассчитать следующим образом:
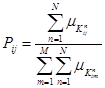
где N — количество переходов, M — количество состояний.
Такой подход является обобщением традиционного подхода к определению вероятности, как отношения числа благоприятствующих событий к общему числу событий. В четкой постановке задачи элементы матрицы вероятностей переходов определялись по той же формуле с той лишь разницей, что для заданных n и i функция принадлежности 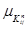 принимала значение 1 для одной единственной комбинации i и j, и 0 — для всех остальных комбинаций.
принимала значение 1 для одной единственной комбинации i и j, и 0 — для всех остальных комбинаций.
Цены состояний определим по формуле:
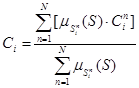
где 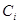 — цена состояния Si (значение показателя в состоянии Si),
— цена состояния Si (значение показателя в состоянии Si), 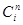 — цена состояния Si на n-м шаге,
— цена состояния Si на n-м шаге, 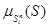 — степень принадлежности системы состоянию Si на n-м шаге, N — количество периодов.
— степень принадлежности системы состоянию Si на n-м шаге, N — количество периодов.
Очевидно, такое определение цен нечетких состояний также является обобщением классического способа определения цен, когда 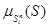 может принимать только значения 0 или 1, а
может принимать только значения 0 или 1, а 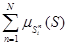 соответствует тому, сколько раз система находилась в состоянии Si за исследуемый период времени.
соответствует тому, сколько раз система находилась в состоянии Si за исследуемый период времени.
Теперь, наложив деформационные матрицы на первоначальную матрицу переходов между нечеткими состояниями, мы можем рассчитать финальные вероятности нечетких состояний системы при применении той или иной стратегии, а также соответствующие математические ожидания экономических показателей.
В том случае, если в реальной задаче имеется достаточное количество пограничных состояний системы, то математические ожидания экономических показателей в нечеткой постановке задачи будут отличаться от четкой постановки, что приведет к принятию других решений, чем те, которые были бы приняты на основе четкой постановки.
Литература:
1. Свешников А. А. Прикладные методы теории марковских процессов. Спб.: Лань, 2007. 192 с.
2. Заде, Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976. 165 с.

