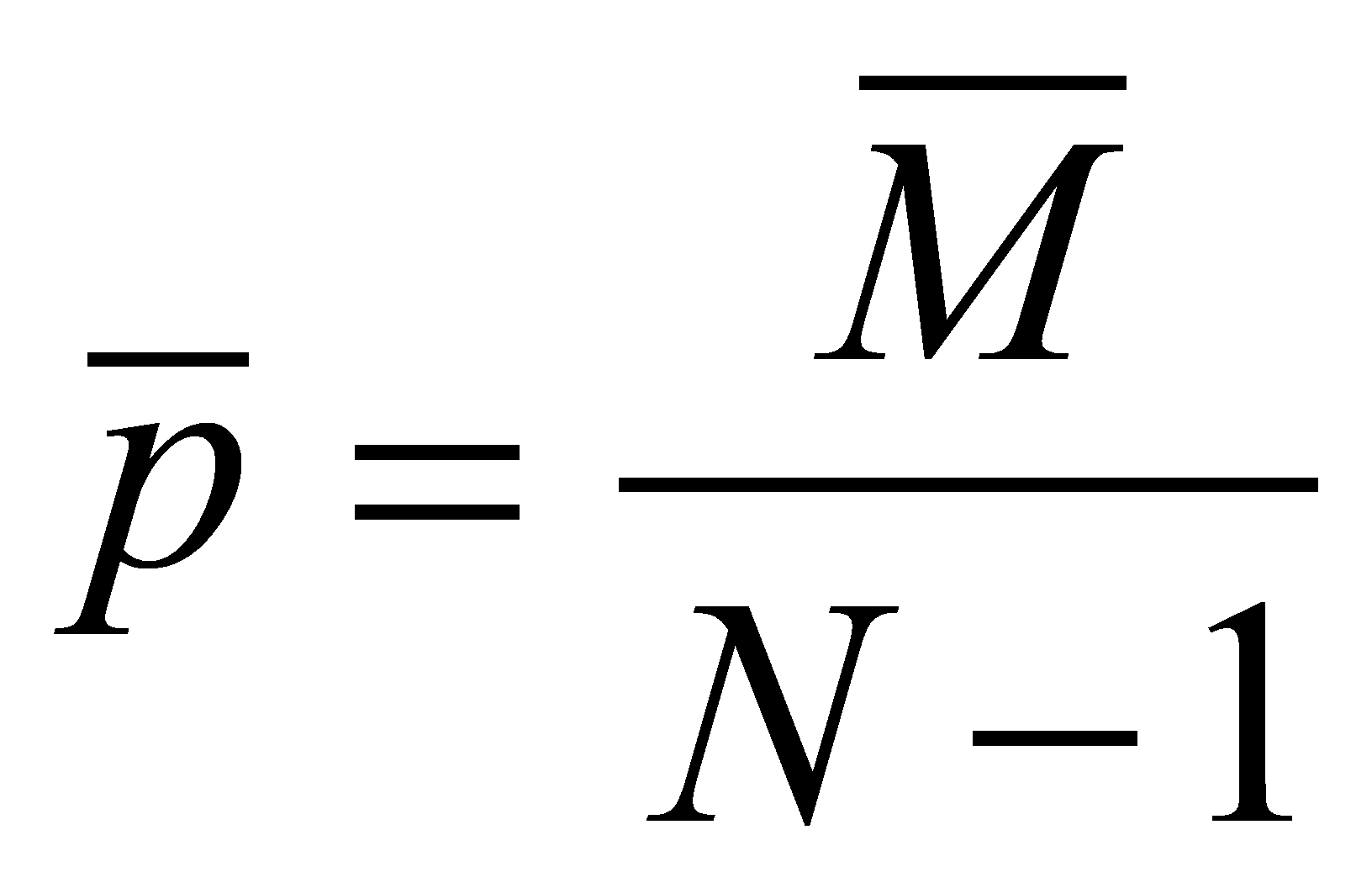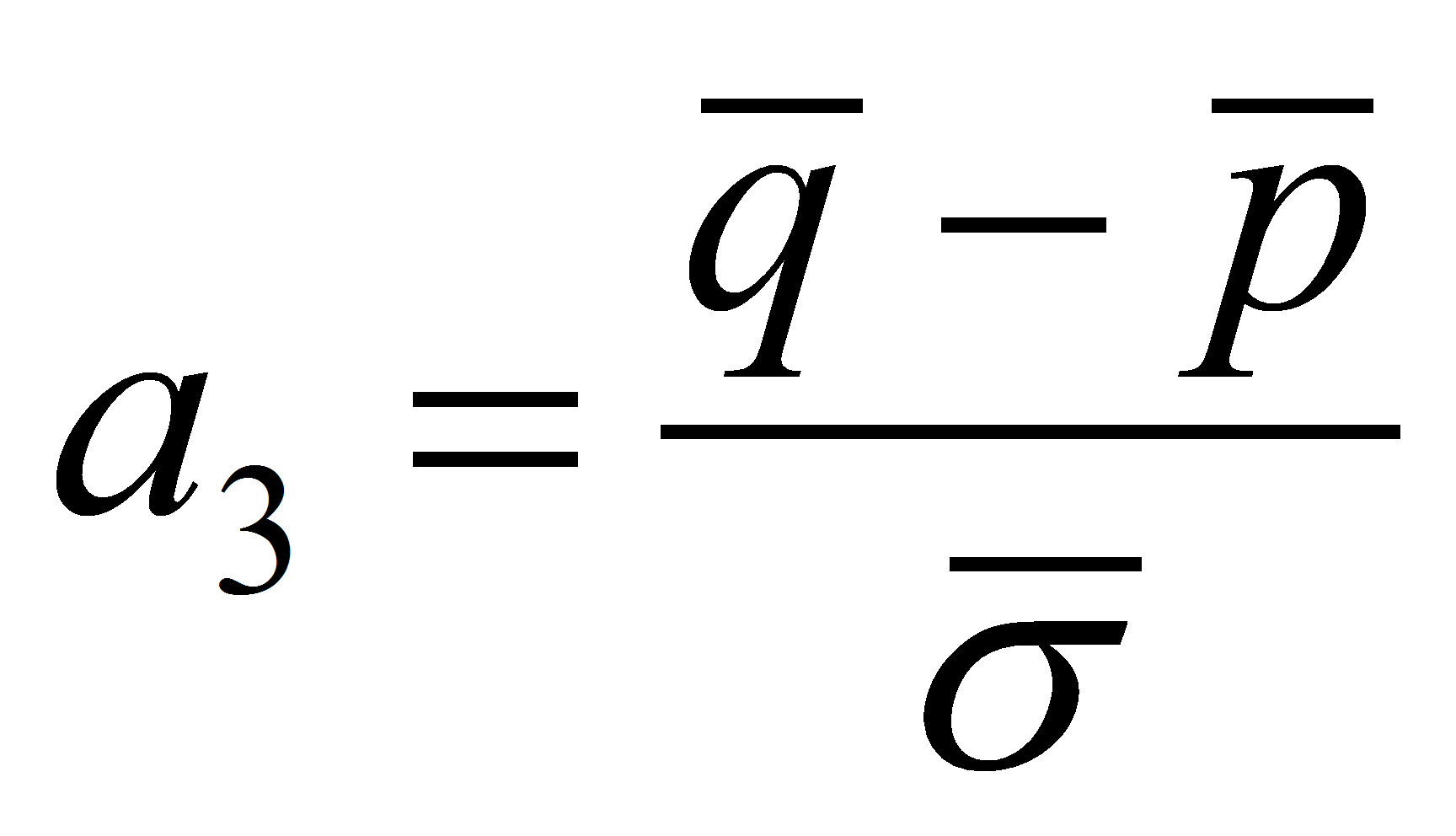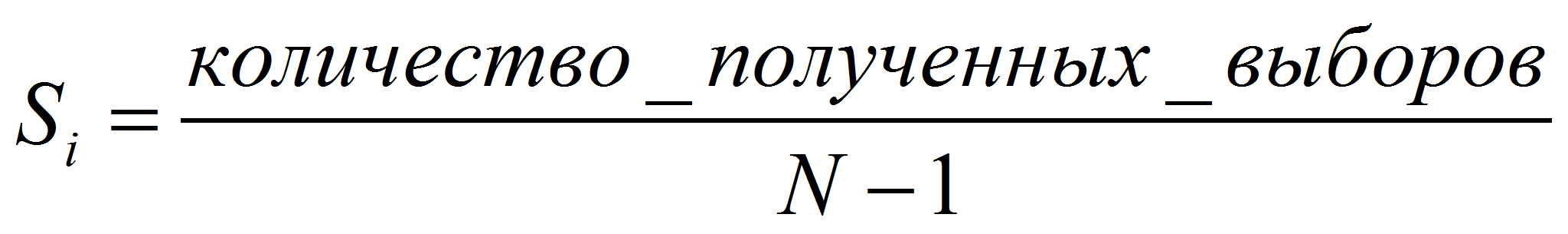Введение. Проведение социометрического исследования строится на постулате, что структуру отношений в коллективе можно выяснить, анализируя выборы партнера для совместной реализации какой-либо деятельности. Такие виды деятельности заранее четко определены и называются социометрическими критериями [1,3].
Актуальность данного вопроса заключается в том, что использование математического аппарата для описания группового поведения увеличивает количество испытуемых, находящихся в исследуемой группе, и дает возможность автоматизации расчетов с помощью информационных технологий.
Целью исследования было проведение социометрии группы студентов с использованием математического аппарата.
Методика и организация исследования. Предложенная методика включает в себя несколько этапов:
- Составление опросного листа с включением вопросов, предусматривающих выбор.
- Проведение инструктажа изучаемого коллектива.
- Осуществление социологического опроса.
- Составление социометрической матрицы.
- Составление социограммы.
- Подсчет социометрических индексов.
- Анализ и интерпретация полученных результатов.
В исследовании использовали следующие социометрические критерии: учебная и трудовая деятельности, досуг. В соответствие с ними был составлен список вопросов:
- ФИО.
- Номер группы.
- Учебная деятельность. С кем из студентов вашей группы вы предпочли бы готовиться к экзаменам?
- Трудовая деятельность. С кем из студентов вы пошли бы работать на производственную практику в коммерческую фирму с условием, что во время практики вам начисляют зарплату, и ее размер зависит от вклада каждого из сотрудников?
- Досуг. С кем из студентов вашей группы вы предпочли бы пойти в поход?
Применяли
параметрический вариант проведения социометрии: число выборов
ограниченно, и рассчитывается по формуле:
![]() ,
,
где d — количество выборов, N — количество людей в группе. Выбор одного и того же сокурсника может повторяться в разных сферах деятельности. В данном случае предусмотрены только положительные выборы, хотя допускается работа и с отрицательными (отвержения).
Данные опроса заносили в социометрическую матрицу, где каждому тестируемому отводиться одна строчка по горизонтали, и одна графа по вертикали. В соответствующих ячейках отмечено количество выборов и общая сумма выборов, сделанных данным респондентом. Клетки по диагонали заштрихованы, так как самовыборы исключаются.
Следующий этап —
составление социограммы, дающей наглядное раскрытие структуры
взаимосвязей в коллективе. Все испытуемые делятся по сумме
полученных выборов на несколько страт. Получившие большинство выборов
относятся к так называемой группе «звезд»,
а получившие мало выборов — к «отвергаемым».
Границы верхних и нижних страт рассчитываются по формуле:
![]() ,
,
где x —
границы доверительного интервала, M —
среднее количество выборов, приходящихся на одного человека,
t-нормированное
отклонение биноминального распределения,
![]() -
выборочное отклонение. Величину t следует
рассматривать как поправочный коофициент, учитывающий отличие
эмпирического распределения от теоретического, и определяемый по
таблице критических значений по Сальвосу [2,4].
-
выборочное отклонение. Величину t следует
рассматривать как поправочный коофициент, учитывающий отличие
эмпирического распределения от теоретического, и определяемый по
таблице критических значений по Сальвосу [2,4].
Для вычисления границ доверительного интервала проводили дополнительные вычисления.
где V — общее количество выборов, сделанных всеми членами группы, N — число членов группы.
где
![]() —
оценка вероятности быть выбранным в группе.
—
оценка вероятности быть выбранным в группе.
где
![]() —
оценка вероятности оказаться невыбранным в группе.
—
оценка вероятности оказаться невыбранным в группе.
где
![]() —
отклонение количества полученных индивидами выборов от среднего их
числа, приходящегося на одного члена группы.
—
отклонение количества полученных индивидами выборов от среднего их
числа, приходящегося на одного члена группы.
где
![]() —
это степень отклонения распределения выборов от случайного.
—
это степень отклонения распределения выборов от случайного.
На основе полученных данных рассчитали социометрические индексы, дающие количественные характеристики отношений каждого члена группы и всей группы в целом.
где
![]() —
социометрический статус члена группы, то есть отношение группы
к одному из его членов.
—
социометрический статус члена группы, то есть отношение группы
к одному из его членов.
Индекс групповой
сплоченности (степень взаимосвязанности членов группы) определяли по
формуле:
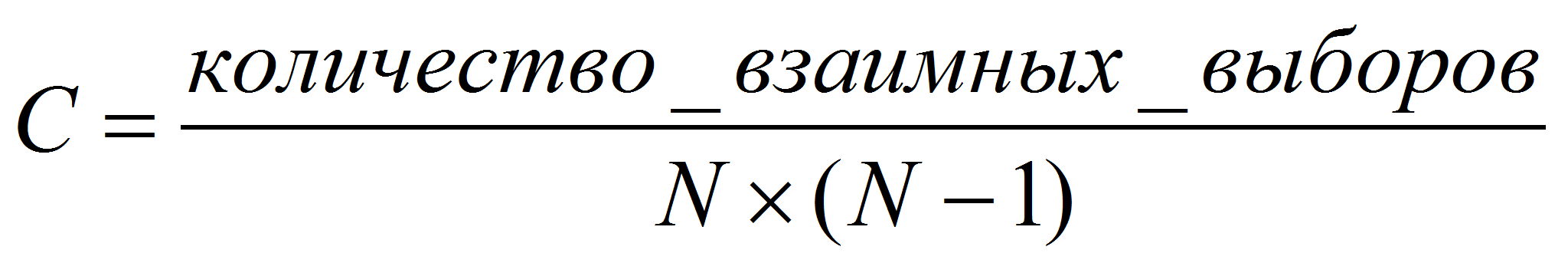 .
.
В исследовании приняли участие 9 студентов I курса специальности педагогика и психология Великолукской академии физической культуры и спорта.
Результаты исследования и их обсуждение. При осуществлении параметрического варианта проведения социометрии мы ограничились двумя выборами, результаты которого приведены в таблице 1.
Таблица 1
Социометрическая матрица
|
|
И. |
А. |
З. |
О. |
Д. |
К.Ц, |
В. |
М. |
К.Н. |
Сумма выборов |
|
И. |
|
2 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
6 |
|
А. |
0 |
|
0 |
0 |
0 |
0 |
3 |
0 |
3 |
6 |
|
З. |
0 |
0 |
|
1 |
0 |
1 |
3 |
0 |
1 |
6 |
|
О. |
0 |
0 |
0 |
|
0 |
0 |
2 |
3 |
1 |
6 |
|
Д. |
1 |
1 |
0 |
1 |
|
0 |
2 |
1 |
0 |
6 |
|
К.Ц. |
0 |
0 |
3 |
0 |
0 |
|
3 |
0 |
0 |
6 |
|
В. |
0 |
0 |
0 |
1 |
0 |
1 |
|
2 |
2 |
6 |
|
М. |
0 |
0 |
0 |
3 |
0 |
0 |
3 |
|
0 |
6 |
|
К.Н. |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
3 |
|
6 |
|
Сумма полученных выборов |
1 |
3 |
3 |
10 |
1 |
3 |
16 |
9 |
8 |
54 |
|
0,125 |
0,375 |
0,375 |
1,25 |
0,125 |
0,375 |
2 |
1,125 |
1 |
|
Полученные
данные внесены в формулы и произведены расчеты: V
= 54; N
= 9;
![]() = 6,75;
= 6,75;
![]()
![]() 0,8438;
0,8438;
![]()
![]() 0,1563;
0,1563;
![]()
![]() 1,0271; a3
1,0271; a3
![]() 0,7; C
0,7; C
![]() 0,097. Для уровня значимости р ≤ 0,05 поправочные коофициенты tmin
= -1,42, tmax
= 1,82; границы верхней и нижней страт хверх
=
9, хниж
=
5.
0,097. Для уровня значимости р ≤ 0,05 поправочные коофициенты tmin
= -1,42, tmax
= 1,82; границы верхней и нижней страт хверх
=
9, хниж
=
5.
Таким образом, получившие 5 или менее выборов приобретают самый низкий социометрический статус, получившие 9 или более — высший. Допуская ошибку не более чем на 5 %, можно утверждать, что лидерами («звезды») являются те, кто получил не менее 9 выборов, получившие от 9 до 5 выборов — принимаемые, а кто получил менее 5 выборов — отвергаемые (табл. 2).
Таблица 2
Отнесение испытуемых к статусной группе
|
Статус |
Инициалы |
|
Звезды |
О., М., В. |
|
Принимаемые |
К.Н. |
|
Аутсайдеры |
И., А., З., К.Ц., Д. |
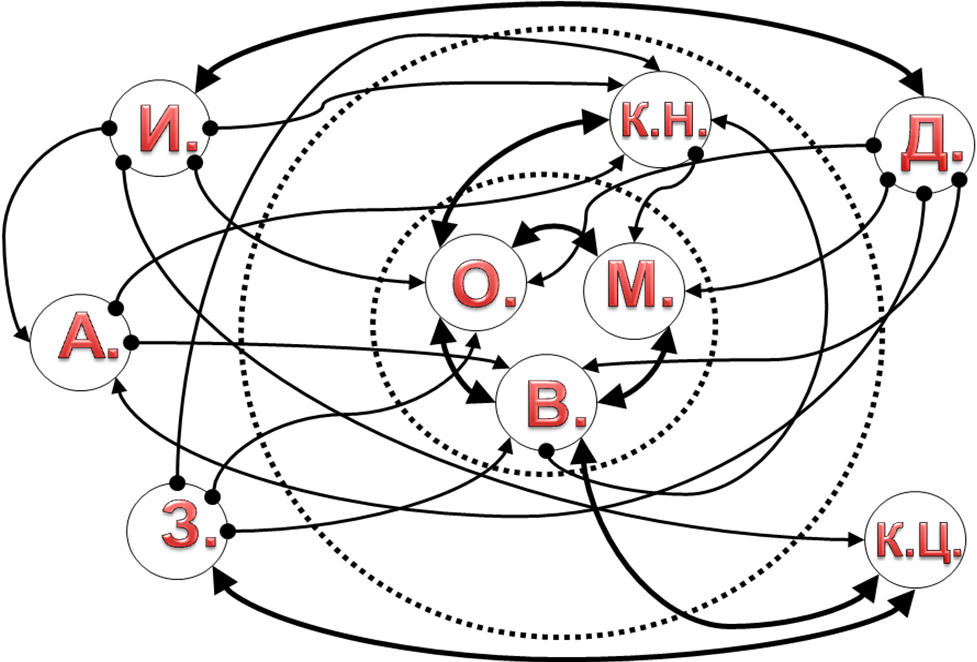
В результате получена информация для составления социограммы (рис. 1).
Рис. 1. Социограмма
Социометрический статус каждого члена группы (Si) приведен в таблице 1. Индекс групповой сплоченности C = 0,097.
Заключение. Таким образом, в исследовании были определены лидеры и отвергаемые группы студентов. Вычислен социометрический статус каждого из испытуемых, и индекс групповой сплоченности. Также составлена социограмма, наглядно показывающую структуру взаимосвязей в коллективе.
В ходе исследования был использован математический аппарат, который в значительной степени упростил анализ результатов, сводя его к подстановке полученных данных в несложные формулы, и дал возможность, в дальнейшем, с помощью информационных технологий ускорить процесс расчетов, и увеличить количество испытуемых.
Литература:
- Кутейников А. Н. Математические методы в психологии. Учебное пособие. — СПб.: Речь, 2008. — 172с.
- Хозиев В. Б. Практикум по общей психологии. Учеб. пособие для вузов /В. Б. Хозиев. — 2-е изд., стереотип. — М.: Академия, 2005. — 272 с.
- Морено Я. Л. Социометрия: Экспериментальный метод и наука об обществе: пер. с англ. / Боковиков А. — М.: Акад. проект, 2001.- 383 с.
- Сидоренко Е. В. Методы математической обработки в психологии. — СПБ.: Речь, 2006. — 350 с.