В статье рассматривается краевая задача с дробно нагруженным уравнением теплопроводности в первом квадранте. Нагрузка имеет форму дробной производной Капуто, и порядок производной меньше порядка дифференциальной части. Обращением дифференциальной части уравнения задача сводится к интегральному уравнению типа Вольтерра второго рода. Ядро полученного интеграла уравнение содержит специальную функцию, а именно вырожденную гипергеометрическую функцию Трикоми. Решение интегрального уравнения обладает некоторым порядком малости при малых значениях времени, причем порядок малости зависит от порядка дробной производной в нагруженном слагаемом.
Ключевые слова : дробная нагрузка, производная, уравнение, интегральное уравнение.
Исследование по дробным дифференциальным уравнениям активно проводилось как в предыдущие десятилетия, так и сейчас интерес к этой области продолжает расти [1–4]. Это связано как развитием самой теории дробного интегрирования и дифференцирования, так и приложениями аппарата дробного интегрирования и дифференцирования в различных областях науки. Решение многих важных задач, например, по оптимальному управлению агроэкосистемой, сводятся к изучению именно таких уравнений [5–6].
Существование и единственность решений дробно-нагруженных краевых задач в определенных функциональных классах зависят от порядка дробной производной в нагруженном слагаемом. Методы исследования базируются на подходе к исследованию краевых задач, основанном на их сведении к интегральным уравнениям. К интегральному уравнению задача сводится обращением дифференциальной части.
Краевые задачи для дробно-нагруженного уравнения теплопроводности, когда нагруженное слагаемое представлено в форме дробной производной, исследованы некоторыми авторами.
1. Постановка дробно-нагруженной краевой задачи теплопроводности
Рассмотрим задачу в области:
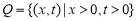
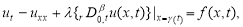
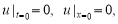
где
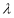
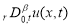
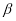
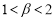
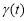
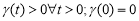
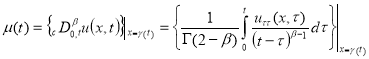
2. Сведение к интегральному уравнению.
Обратим дифференциальную часть задачи (1)-(2).
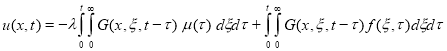
Получим
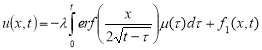
От (4) найдем производную Капуто порядка
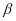
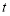
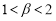
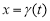
Предварительно вычислим
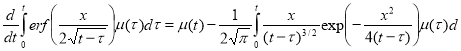
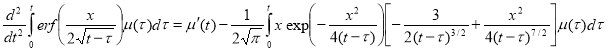
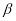
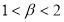
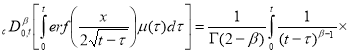
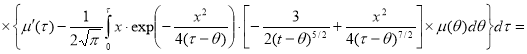
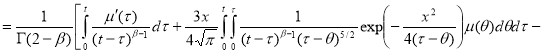
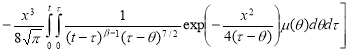
Первый интеграл вычисляем интегрированием по частям, во 2-м и 3-м интеграле меняем порядок интегрирования
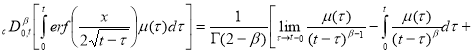
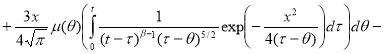
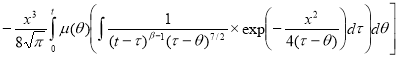
Потребуем при
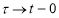
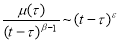
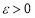
Тогда
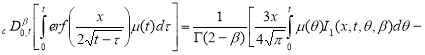
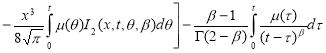
Где
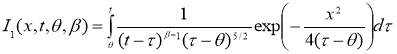
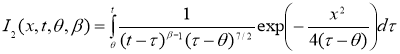
Замена
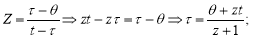
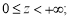
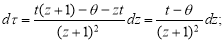
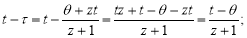
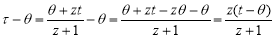
Тогда
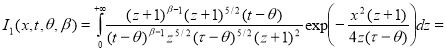
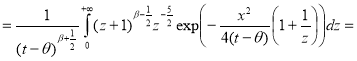
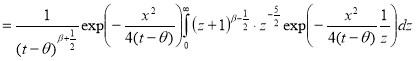
Замена:
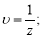
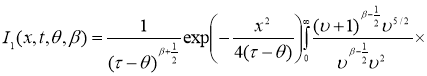
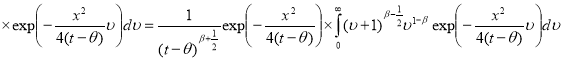
Нахушев А. М. Уравнения математической биологии — [1, с. 286]; формула 2.3.6 (9)
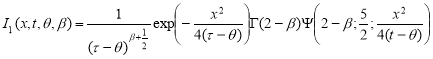
Аналогично получим
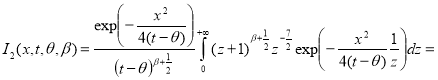
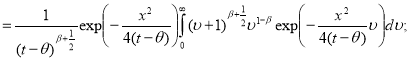
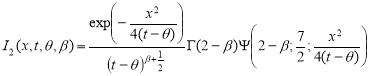
Здесь
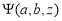
Подставив выражения (6) и (7) в (5), получим:
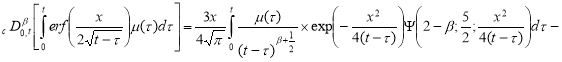
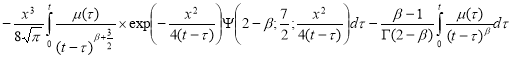
С учетом (8) при
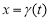
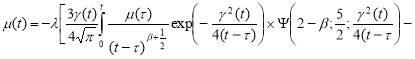
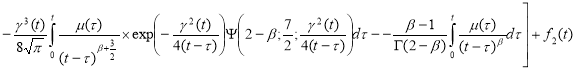
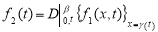
или
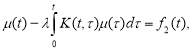
Где
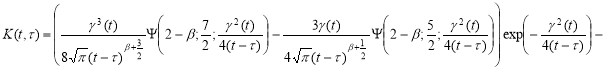
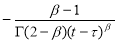
Преобразуем выражение в фигурных скобках в равенстве (11) обозначив его через
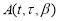
Обозначим
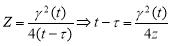
Тогда
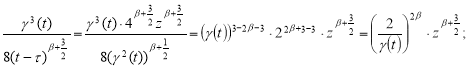
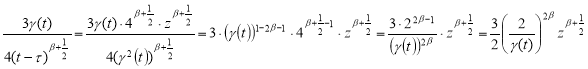
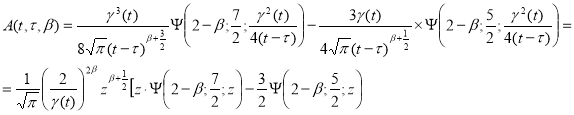
(12)
Введем обозначения согласно [Бейтман 1]
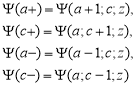
Тогда согласно формуле (7) и (6) из [Бейтман 1, стр. 246]
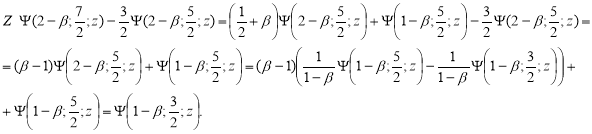
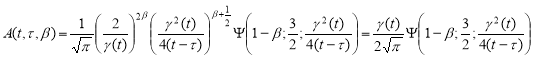
Тогда ядро (11) можно переписать виде
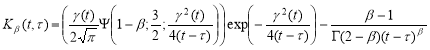
Основной результат
Лемма
Краевая задача (1)-(2) эквивалентно сводится к интегральному уравнению Вольтерра (11) с ядром и правой частью, определяемыми формулами (9) и (13) соответственно, где
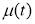
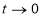
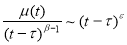
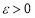
Литература:
- Нахушев А. М. Уравнения математической биологии. — М.: Высшая школа, 1995.
- Нахушев А. М. Нагруженные уравнения и их приложения // Дииференц. уравнения. — 1983.
- Нахушев А. М. О задаче Дарбу для одного вырождающегося нагруженного интегро-дифференциального уравнения. — 1976.
- Дженалиев М. Т. К теории линейных краевых задач для нагруженных дифференциальных уравнений. — Алматы: Компьютерный центр ИТПМ, 1995.
- Дженалиев М. Т. О нагруженных уравнениях с периодическим граничными условиями // Дифференц. уравнения. — 2001. — Т.37, № 1. — С.48–54.
- Дженалиев М. Т. Рамазанов М. И. Нагруженные уравнения — как возмущения дифференциальных уравнения. — Алматы: ГЫЛЫМ, 2010.
- Oldham K. B., Spainer J. The Fractional Calculus. — New York-London: Academic Press, 1974.
- Самко С. Г., Килбас А. А., Марчев О. И. Интегралы и производные дробного порядка и некоторые их приложения. — Минск: Наука и техника, 1987.
- Космакова М. Т., Касымова Л. Ж. К решению уравнения теплопроводности с дробной нагрузкой. — Вестник КазНУ. Серия математика, механика, информатика. № 1 (101), 2010.

