В работе исследована обратная задача определения правой части для дифференциального уравнения с частными производными четвертого порядка с переопределениям во внутренних точках. Сначала с помощью функции Грина исходная прямая задача сводится к эквивалентной задаче, для которой доказывается теорема существования и единственности решения. Далее, пользуясь методами обратных теории задач, доказывается существование и единственность решения рассматриваемой обратной задачи.
Ключевые слова: обратная задача, дифференциального уравнения с частными производными, функция Грина.
К настоящему времени обратные задачи превратились в бурно развивающуюся область знаний, проникающую почти во все сферы математики, включая алгебру, анализ, дифференциальные уравнения, математическую физику и др. С другой стороны, теория обратных задач широко применяется для решения практических задач почти во всех областях науки, в частности, в физике, медицине, экологии, экономике.
На данный момент в связи с проблемами геофизики, океанологии, физики атмосферы, использованием криогенных жидкостей в технике и ряда других проблем значительно возрос интерес к изучению динамики неоднородных, и в частности, стратифицированных жидкостей, которые приводят к начально-краевым задачам для уравнений с частными производными четвертого порядка.
В работе рассматривается обратная задача для дифференциальных уравнений с частными производными четвертого порядка.
Постановка задачи. Требуется найти функции f(t) иu(t,x) в области
ΩT={(x, t)|0<x<1,![]() },удовлетворяющие уравнению
},удовлетворяющие уравнению
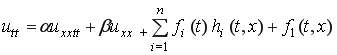 ,(1)
,(1)
заданным начальным и краевым условиям,
![]() ,
,![]() ,
,![]() ,(2)
,(2)
![]() (3)
(3)
и известно решениеu(t,x) в точке![]()
![]()
![]()
![]() ,(4)
,(4)
где 0<T — заданная постоянная,αиβ- известные постоянные.
Предположим выполнение следующих условий:
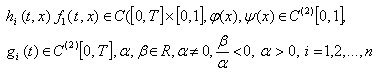 (5)
(5)
Лемма 1. Если![]() то резольвентаR(t,s)ядра
то резольвентаR(t,s)ядра![]() ,
, ![]() представима в виде
представима в виде
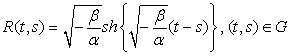 .(6)
.(6)
Доказательство.Для докакзательства покажем, что
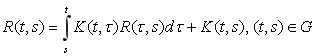 .
.
В самом деле,
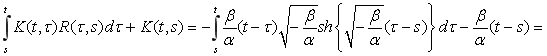
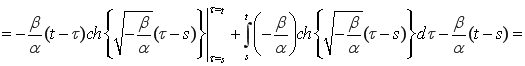
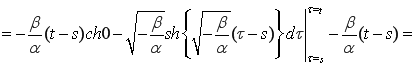
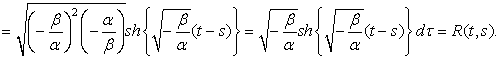
Лемма 1 доказана.
Лемма 2. Если α>0, то функция Грина краевой задачи
![]()
записывается в виде
 (7)
(7)
Доказательство.Функцию Грина G(x,) будем искать в виде
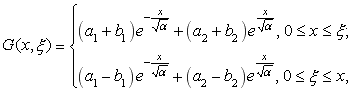 (8)
(8)
где a1,a2,b1,b2 — пока неизвестные функции.Из определения функции Грина G(x,) имеем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Продифференцируем (8) по х:
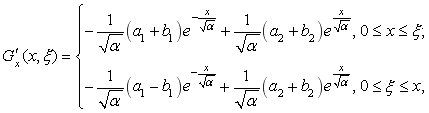
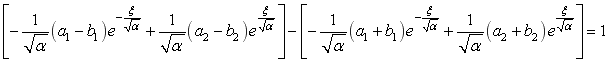 Тогда
Тогда
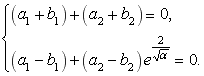
Отсюда находим
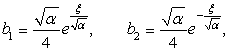 (9)
(9)
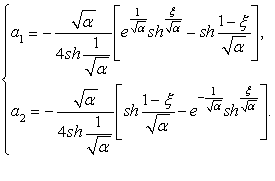 (10)
(10)
Подставляя (9) и (10) в (8), получим (7). Лемма 2 доказана.
Для решения обратной задачи (1)-(4) введем обозначение
![]() (11)
(11)
Тогда имеют место равенства
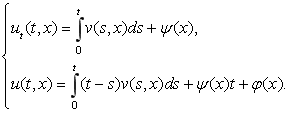 (12)
(12)
Учитывая (11) и (12), из (1) имеем
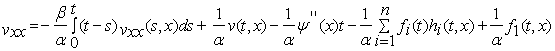 . (13)
. (13)
Применяя резольвенту (5) ядра ![]() ,
, ![]() из (12) получим
из (12) получим
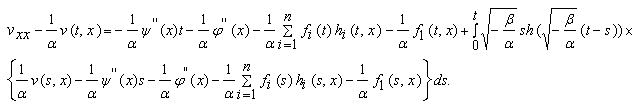 (14)
(14)
![]() Учитывая (3), из (11) имеем
Учитывая (3), из (11) имеем
![]() (15)
(15)
Используя функцию ГринаG(x,) определенную по формуле (7)к краевой задаче (14)-(15), получим
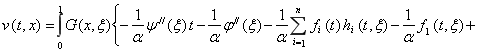
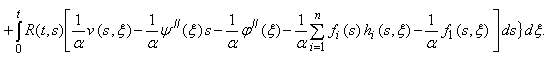 (16)
(16)
![]() Введя обозначение для известных функций
Введя обозначение для известных функций
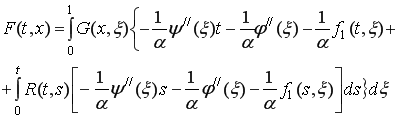 (17)
(17)
уравнение (16) перепишем в виде
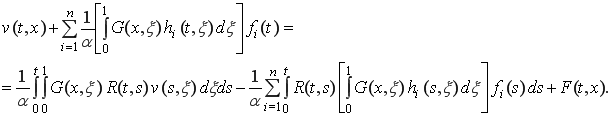 (18)
(18)
![]() Полагая
Полагая ![]()
![]() иучитывая (4), (11), из (18) имеем
иучитывая (4), (11), из (18) имеем
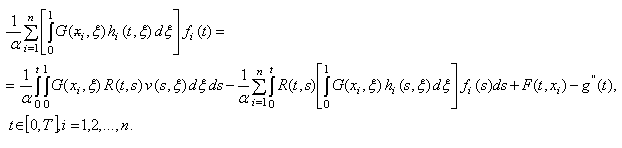 (19)
(19)
![]()
![]() Пусть
Пусть
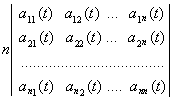
![]() где
где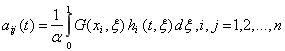 (20)
(20)
Таким образом, для определения![]() и v(t,x),
и v(t,x),![]() ,
,![]() мыполучили систему линейных интегральных уравнений Вольтерра второго рода (18) и (19).Тем самым доказана следующая
мыполучили систему линейных интегральных уравнений Вольтерра второго рода (18) и (19).Тем самым доказана следующая
Теорема. Пусть выполняются условия (5) и (20). Тогда обратная задача (1)-(4) имеет единственное решение {v(t,x),f(t),![]() }из пространства
}из пространства![]() где
где ![]() пространство n- мерных вектор- функций с элементами из
пространство n- мерных вектор- функций с элементами из ![]()
Литература:
- Asanov A., Atamanov E. R. Nonclassical and Inverse Problems for Pseudoparabolic Equations. — Netherlands: VSP, Utrecht, 1997. — 152 p.
- Асанов А., Атаманов Э. Р. Обратная задача для операторного интегро-дифференциального псевдопараболического уравнения.- Сиб. матем. журнал.- 1995. Т.36. № 4.- С.752–762.
- Бухгейм А. Л. Уравнения Вольтерра и обратные задачи. — Новосибирск: Наука, 1983. — 207 с.
- Кабанихин С. И. Обратные и некорректные задачи. — Новосибирск: Сибирское научное издательство, 2009. — 457 с.
- Лаврентьев М. М. О некорректных задачах математической физики.- Новосибирск: СО АН СССР, 1962.
- Матанова К. Б. Обратная задача для дифференциальных уравнений с частными производными четвертого порядка // Вестник ОшГУ. Труды международной научно-теоретической конференции “Проблемы образования, науки и культуры в начале 21 века”. 2001. Вып. 4. — С. 94–100.

