Работа посвящена исследованию одной граничной обратной задаче для уравнения теплопроводности, которое связана с изучением нестационарных тепловых процессов. Обратная задача заключается в нахождении граничной функции из первой начально-краевой задачи для уравнения теплопроводности по переопределению во внутренней точке. Задача сводится к интегральному уравнению Вольтерра первого рода. Методом кавзиобращение доказывается сходимость приближенного решения к точному решению и получена соответствующая оценка погрешности.
Ключевые слова: параболическое уравнение, обратные задачи, неизвестные граничные данные, переопределение во внутренней точке обратная граничная задача теплопроводности.
The work is devoted to the study of one boundary inverse problem for the heat equation, which is associated with the study of non-stationary thermal processes. The inverse problem consists of finding the boundary function from the first initial-boundary value problem for the heat equation by redefinition at an internal point. The problem is reduced to the Volterra integral equation of the first kind. Using the causi-inversion method, the convergence of the approximate solution to the exact solution is proved and the corresponding error estimate is obtained.
Keywords: parabolic equation, inverse problems, unknown boundary data, redefinition at the internal point of the inverse boundary value problem of heat conduction.
В задачах, связанных с исследованием нестационарных тепловых процессов, довольно часто встречается ситуация, когда невозможно провести прямые измерения требуемой физической величины и ее характеристики определяются по результатам некоторых косвенных измерений. При этом единственным методом нахождения требуемых значений связан с решением граничной обратной задачи теплопроводности с исходными данными, известными только на части границы. Аналогичные граничные обратные задачи возникают не только при изучении тепловых процессов, но и при исследовании процессов диффузии, изучении свойств материалов, связанных с тепловыми характеристиками.
В работе рассматривается граничная обратная задача для уравнения теплопроводности, которая сводится к интегральному уравнению Вольтерра первого рода. К этой задаче применяется метод квазиобращения, где в качестве возмущенного уравнения рассматривается псевдопараболическое уравнение [1]. Различные обратные задачи, в том числе граничные изучены в работах [1–5]. Отметим, что метод квазиобращение разработан французскими математиками Р.Латтесом и Ж.-Л.Лионсом и подробно изложены в монографии [6].
Граничные обратные задачи для параболических уравнений, в частности для уравнения теплопроводности изучались многими авторами, в частности в работах [7–12] исследованы граничные обратные задачи теплопроводности, а задача о колебаниях стержня с неизвестным условием его закрепления на части границы для исследованы в работе [14].
- Постановка обратной задачи и сведение обратной задачи к интегральному уравнению первого рода
Пусть
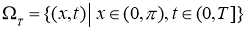
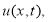
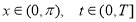
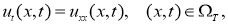
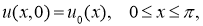
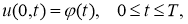
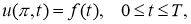
где
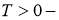
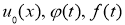
Обратная задача.
Найти пару функций
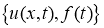
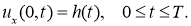
Определение 1.1.
Пара функций
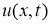
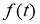
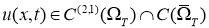
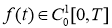
2. Корректность прямой задачи
Сначала покажем корректность прямой задачи (1)-(3).
Теорема 2.1.
Пусть
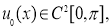
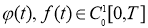
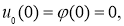
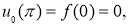
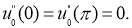
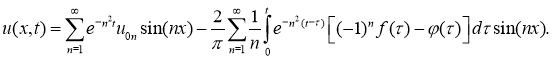
где
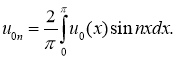
Доказательство.
Для заданной функции
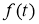
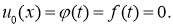
Действительно, вместо функции
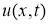
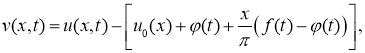
которая удовлетворяет задаче
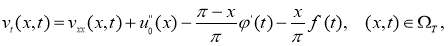
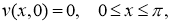
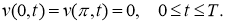
Согласно, методу Фурье ([см.3, с.243]). решение задачи (5) — (8) ищем в виде
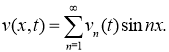
Тогда для определения функции
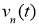
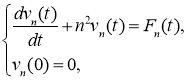
где
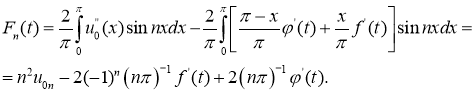
Решая задачу (11) и учитывая (12), после интегрирования по частям, имеем
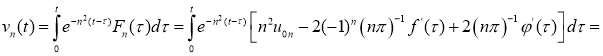
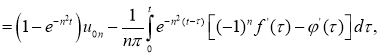
Подставляя (1.13) в (1.10), находим
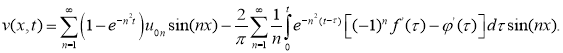
Тогда подставляя (14) в (6) и после несложных преобразований, получим
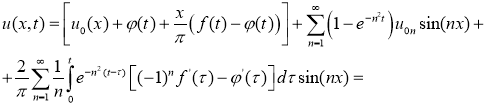
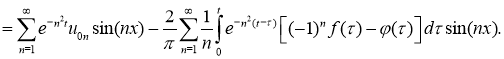
Как и в работе [5], в силу условий, наложенных на функции
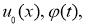
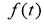
Так как
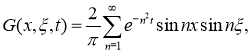
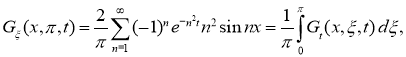
то формулу (15) можно переписать в виде
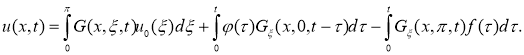
Обозначим
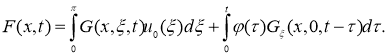
Тогда
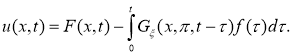
Задача нахождения граничной функции является некорректной задачей.
Действительно, продифференцируем выражение (16) по
х,
затем положим в полученное выражение
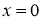
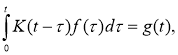
где
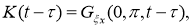
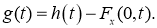
Таким образом, задача нахождения граничного условия для уравнения теплопроводности поставлено некорректно [1].
- Метод квазиобращения и оценка погрешности приближенного решения
Для приближенного решения некорректной задачи используем псевдопараболический вариант квазиобращения [1]. В этом пункте рассмотрим вопрос регуляризации следующей некорректной граничной обратной задачи нахождения пару функций
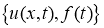
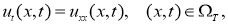
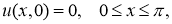
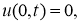
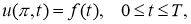
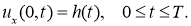
Здесь
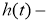
Так как задача (18)-(21) некорректна, то для заданной функции
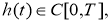
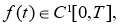
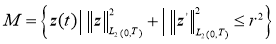
но функция
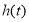
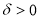
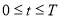
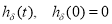
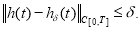
Требуется построить приближенное решение обратно задачи (18)-(21) и оценить разность между точным и приближенным решением.
Покажем, что в качестве приближенного решения обратной задачи (18) — (21) может быть взята функция
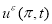
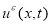
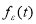
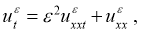
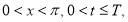
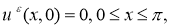
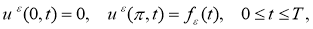
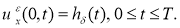
2.1. Исследование обратной задачи и оценка погрешности
Приведем результат об однозначной разрешимости задачи(23) — (25).
Т
еорема 2 [4].
Пусть функция
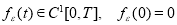
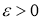
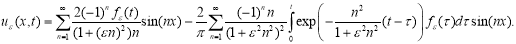
А для обратной задачи (23) — (26) справедлива
Теорема 3.
Пусть
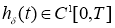
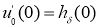
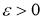
Доказательство. Согласно результата работы [2], решение задачи (23) — (26) существует, единственно и представимо явной формулой:
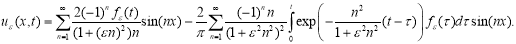
Пусть
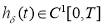
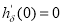
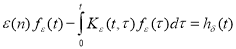
где
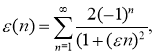
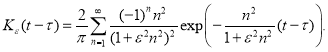
Уравнение (30) при каждом
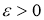
пространстве
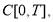
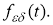
2.2. Метод квазиобращения. Для приближенного решения некорректной задачи используем псевдопараболический вариант метода квазиобращения [1]. В отличие от обычного варианта метода квазиобращения [6], здесь не требуется дополнительные граничные условия.
Теорема 2.
Пусть функция
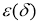
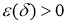
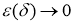
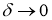
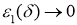
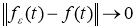
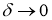
Доказательство.
Обозначим через
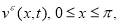
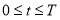
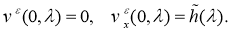
Применив к обратной задаче (18)-(21) преобразование Фурье, получим следующую обратную задачу:
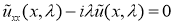
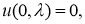
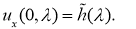
где
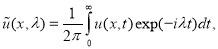
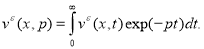
Решением задачи (31), (32) является
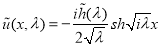
Применяя к обратной задаче (22), (23), (26) преобразование Фурье, получим следующую задачу Коши:
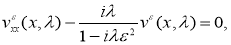
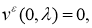
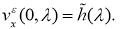
Решением задачи (2.17), (218) является функция
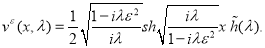
Таким образом, в качестве приближенного решения исходной граничной обратной задачи берется функция
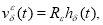
где Фурье образ функции
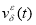
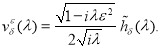
Здесь
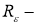
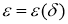
Рассмотрим оценку погрешности приближенного решения граничной обратной задачи на множестве
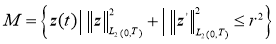
Используем методику работы [15]. В качестве характеристики точности приближенного решения используем величину
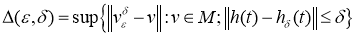
Далее, используем очевидную оценку
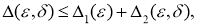
где
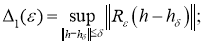
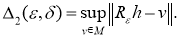
Рассмотрим функцию
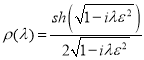
Так как
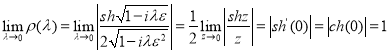
то существует такое
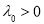
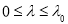
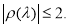
Следовательно,
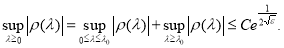
где
C —
постоянная, не зависящая от
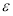
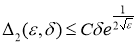
А для
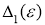
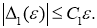
Выберем зависимость
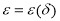
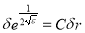
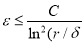
Тогда как и в работе [15] можно доказать, что существуют такие числа
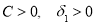
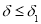
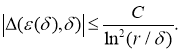
Из оценки (37) с учетом оценки погрешности оптимального метода решения обратной граничной задачи на множестве M, полученной в работе [2], доказана следующая теорема
ТЕОРЕМА 4
. Пусть точное решение задачи (18)-(21) непрерывно на отрезке
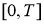
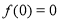
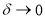
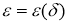
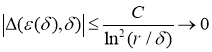
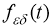
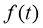
Литература:
1. Аблабеков, Б. С. Обратные задачи для псевдопараболических уравнений / Б. С. Аблабеков. — Бишкек: Илим, 2001. –183 с.
2. Аблабеков Б. С. Граничная обратная задача для уравнения фильтрации жидкостей в трещиноватом пласте // Известия Кыргызского государственного технического университета им. И.Раззакова. 2013. № 28. С. 449–452.
3. Аблабеков, Б. С. Метод полуобращения и существование решений начальной, начально-краевой задачи /Б. С. Аблабеков // Наука и новые технологии. –1999.- № 4. — С. 12– 19.
4. Аблабеков, Б. С. Первая начально-краевая задача для одномерного псевдопараболического уравнения с малым параметром [Текст] / Б. С. Аблабеков, А. Т. Муканбетова // Евразийское Научное Объединение. 2019.Т. 1. № 4 (50), C.1–5.
5. Аблабеков, Б. С. О разрешимости граничной обратной задачи для псевдопараболического уравнения [Текст] / Б. С. Аблабеков, А. Т. Муканбетова // Евразийское научное объединение. –2021. Т.1. –№ 7(77). –С.5 –8.
6. Латтес, Р. Метод квазиобращения и его приложения / Р. Латтес, Ж.-Л. Лионс. — М.: Мир,1970. — 336 с.
7. Вабищевич, П. Н. Разностные методы решения граничной обратной задачи теплопроводности / П. Н. Вабищевич // Дифференц. уравнения, 1991, том 27, номер 7, 1114–1123.
8. Костин, А. Б. О некоторых задачах восстановления граничного условия для параболического уравнения I /А. Б. Костин, А. И. Прилепко // Дифференц. уравнения. -1996.-Т.32, № 1.-С.107–116.
9. Костин, А. Б. О некоторых задачах восстановления граничного условия для параболического уравнения /А. Б. Костин, А. И. Прилепко // Дифференц. уравнения. -1996.-Т.32, № 11.-С.1519–1528.
10. Щеглов А. Ю. О равномерном приближении решения одной обратной задачи методом квазиобращений / А. Ю. Щеглов // Матем. заметки, 1993, том 53, выпуск 2, 168–174.
11. Щеглов А. Ю. Метод решения обратной граничной задачи динамики сорбции с учетом диффузии внутри зерна / А. Ю. Щеглов //Ж. вычисл. матем. и матем. физ., 2002, том 42, номер 4, 580–590.
12. Солодуша С. В. Численное решение обратной граничной задачи теплопроводности с помощью уравнений Вольтерра I рода /С. В. Солодуша, Н. M. Япарова, // Сиб. журн. вычисл. матем., 2015, том 18, номер 3, 327–335
13. Япарова Н. М. О различных подходах к решению обратных граничных обратных задач тепловой диагностики / Н. М. Япарова //Вестн.ЮУрГУ. Сер».Математика. Механика, Физика». — 2012.-№ 34.– С.60–67.
14. Бейлина, А. Б. Задача о колебаниях стержня с неизвестным условием его закрепления на части границы / А. Б. Бейлина, Л. С. Пулкина //Вестник Самарского университета. Естественнонаучная серия.2017, № 2. С.7–14.
15. Табаринцева Е. В. О решении граничной обратной задачи для параболического уравнения методом квазиобращения / Е. В. Табаринцева, Л. Д. Менихес, А. Д. Дрозин//Вестн.ЮУрГУ. Сер».Математика. Механика, Физика». — 2012.-№ 11.– С.8–13.

