Квантовое сужение, создаваемое в двухмерной гетероструктуре, ограничивая движение носителей узкой областью пространства, изменяет свойства не только доноров или экситонов [1,2], но и двухэлектронных 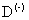 ,
, 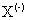 центров. Например, в полупроводниковых гетроструктурах GaAs/AlGaAs наблюдался значительный рост энергии связи
центров. Например, в полупроводниковых гетроструктурах GaAs/AlGaAs наблюдался значительный рост энергии связи 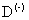 центров в условиях гибридного квантования [3].
центров в условиях гибридного квантования [3].
Для расчета энергии связи многочастичных центров 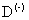 ,
, 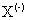 в приближении эффективной массы обычно используют вариационные методы [4–6]. Более точные расчеты обычно требуют введения значительного количества вариационных параметров в волновую функцию системы [4,6]. В некоторых случаях для расчета энергии связи
в приближении эффективной массы обычно используют вариационные методы [4–6]. Более точные расчеты обычно требуют введения значительного количества вариационных параметров в волновую функцию системы [4,6]. В некоторых случаях для расчета энергии связи 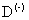 ,
, 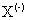 комплексов, можно воспользоваться более простыми пробными функциями. Волновая функция Чандрасекара, которая применяется в работе [5], содержит всего три параметра и имеет вид
комплексов, можно воспользоваться более простыми пробными функциями. Волновая функция Чандрасекара, которая применяется в работе [5], содержит всего три параметра и имеет вид
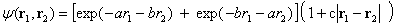 (1)
(1)
Симметризованная по координатам электронов (с учетом спина — антисимметричная) функция (1) напоминает корреляционное движение двух электронов, которые находятся на различных орбитах. При расчете энергии 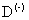 центра можно также воспользоваться трехпараметрической волновой функцией Хиллерааса
центра можно также воспользоваться трехпараметрической волновой функцией Хиллерааса
 (2)
(2)
В данном случае корреляционное движение двух электронов происходит в одной орбите.
Расчет на основе (2) полной энергии двухмерного (2D) и трехмерного (3D)  центра, энергии связи (отрыва) одного электрона и сравнение полученных результатов является целью данной работы.
центра, энергии связи (отрыва) одного электрона и сравнение полученных результатов является целью данной работы.
 центр напоминает отрицательного иона атома водорода
центр напоминает отрицательного иона атома водорода 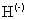 и состоит из ионизованного донорного атома и двух электронов, движущихся в поле этого заряда. Гамильтониан этой системы имеет вид
и состоит из ионизованного донорного атома и двух электронов, движущихся в поле этого заряда. Гамильтониан этой системы имеет вид
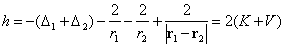 (3)
(3)
Здесь энергия и длина измеряются в единицах
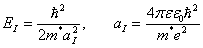 (4)
(4)
Аналогично 3D случаю (см. [7,8]) переходим от переменных
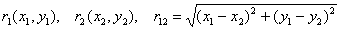
к новым переменным
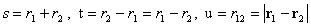 .
.
Окончательные результаты имеет вид
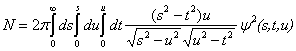 ,
,
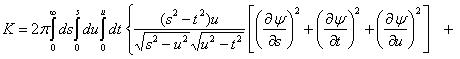
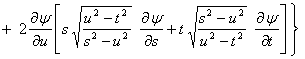 ,
,
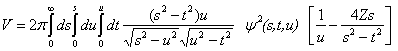
В 3D и 2D случаях вычисленные с помощью пробной функции (2) полные энергии 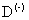 центра соответственно равны
центра соответственно равны 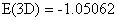 и
и 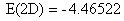 , т. е. при понижении размерности системы полная энергия возросло примерно
, т. е. при понижении размерности системы полная энергия возросло примерно 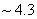 раза.
раза.
Поскольку полная энергия 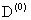 центра в 2D случае равно
центра в 2D случае равно 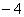 , то энергия связи (отрыва) одного электрона
, то энергия связи (отрыва) одного электрона 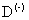 центра должна быть
центра должна быть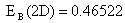 . Более точное значение для
. Более точное значение для 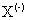 триона было получено с использованием 22 варьируемых параметров [4], оно в пределе
триона было получено с использованием 22 варьируемых параметров [4], оно в пределе 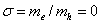 близко к нашему результату.
близко к нашему результату.
Литература:
1. Воробьев Л. Е., Ивченко Е. Л., Фирсов Д. А., Шалыгин В. А. Оптические свойства наноструктур: Учеб. Пособие / Под ред. Е. Л. Ивченко и Л. Е. Воробьева. СПб.:Наука, 2001.–188 с.
2. Шик А. Я., Бакуева Л. Г., Мусихин С. Ф., Рыков С. А. Физика низкоразмерных систем / Под ред. А. Я. Шика. СПб.: Наука, 2001. 160 с.
3. S. Huant, S. P. Najda, Phys. Rev. Lett., 65 (12), 1486 (1990)
4. B. Stebe, A. Ainane, Superlatt. Microstruct., 5 (4), 545 (1989)
5. Сергеев Р.А, Сурис Р.А, ФТТ., 43, 714 (2001). [R. A. Sergeev,R. A. Suris. Phys.Sol.St., 43, 746 (2001)].
6. J. Usukura, Y. Suzuki, K. Varga. Phys. Rev. B, 59 (9), 5652(1999).
7. М. Г. Веселов, Л. Н. Лабзовский. Теория атома. Строение электронных оболочек. М.: Наука. 328 с. (1986)
8. Ф. М. Морс и Г. Фешбах, Методы теоретической физики, т.2. ИЛ, М., (1959)

