В некоторых полупроводниках, например Si, Ge, PbTe, эффективные массы электронов вблизи дна зоны проводимости сильно анизотропны 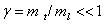 [1]. Для расчета энергии связи мелкого
[1]. Для расчета энергии связи мелкого 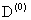 центра в приближении эффективной массы обычно используют вариационные методы [2,3]. Задача сильно усложняется в случае
центра в приближении эффективной массы обычно используют вариационные методы [2,3]. Задача сильно усложняется в случае 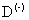 центров: необходимо одновременно учитывать межэлектронную корреляцию и анизотропию.
центров: необходимо одновременно учитывать межэлектронную корреляцию и анизотропию.
Квантовое сужение также сильно влияет на энергию двухэлектронных центров. Так, например, в полупроводниковых гетроструктурах GaAs/AlGaAs наблюдается значительный рост энергии связи 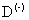 центров в условиях гибридного квантования [4]. Из-за анизотропии масс даже расчет одноэлектронного спектра в сферической квантовой точке Si требует численных методов [5].
центров в условиях гибридного квантования [4]. Из-за анизотропии масс даже расчет одноэлектронного спектра в сферической квантовой точке Si требует численных методов [5].
В настоящей работе для расчета полной энергии (а также энергия отрыва одного электрона) анизотропного 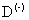 центра применяется вариационный метод Монте-Карло (МК), который широко применяется в расчетах энергии атомных и молекулярных систем [6–9]. Гамильтониан этой системы имеет вид
центра применяется вариационный метод Монте-Карло (МК), который широко применяется в расчетах энергии атомных и молекулярных систем [6–9]. Гамильтониан этой системы имеет вид
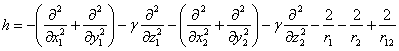 (1)
(1)
Здесь, энергия и длина измеряются в единицах
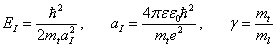 (2)
(2)
Волновую функцию представим в виде
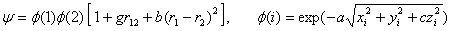 , (3)
, (3)
где величины r1- и r2-, соответственно радиус-векторы первого и второго электронов, а r12 – расстояние между ними. В (1) и (3) анизотропия учтена в одноэлектронных функциях 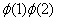 , множитель в квадратной скобке описывает корреляции в движениях двух электронов. Согласно вариационному принципу, параметры a, c, g, bи полная энергия системы определяются из условий минимума функционала
, множитель в квадратной скобке описывает корреляции в движениях двух электронов. Согласно вариационному принципу, параметры a, c, g, bи полная энергия системы определяются из условий минимума функционала
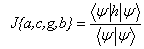 (4)
(4)
В изотропных двухмерных 2D (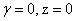 ) и трехмерных 3D (
) и трехмерных 3D (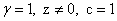 ) пределах интегралы в функционале (4) вычисляется в координатах Хиллерааса (для 3D случая, см. например [10,11]).
) пределах интегралы в функционале (4) вычисляется в координатах Хиллерааса (для 3D случая, см. например [10,11]).
В расчетах общее количество МК шагов составляет 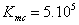 , а количество термализационных шагов равно
, а количество термализационных шагов равно 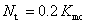 . Усреднения локальной энергии проводились по стандартному алгоритму Метрополиса
. Усреднения локальной энергии проводились по стандартному алгоритму Метрополиса
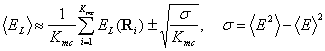 (5)
(5)
Здесь 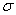 - дисперсия, Ri — координаты точки блуждания в i–м шаге МК. Выражения для локальной энергии и плотности вероятности имеют вид
- дисперсия, Ri — координаты точки блуждания в i–м шаге МК. Выражения для локальной энергии и плотности вероятности имеют вид
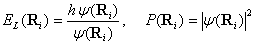 (6)
(6)
и согласно (1) и (3) их можно определить аналитически. Шаги блуждания полагали анизотропными 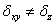 и их значения определены в этапе термализации так, чтобы количество принятых состояний
и их значения определены в этапе термализации так, чтобы количество принятых состояний  приблизительно составляло половину
приблизительно составляло половину  . Параметры кремния и германия используемые в расчетах приведены в таблице.
. Параметры кремния и германия используемые в расчетах приведены в таблице.
Таблица 1
|
|
|
|
|
| |
|
Ge |
0.082 |
1.58 |
0.0519 |
16.0 |
4.36 |
|
Si |
0.190 |
0.98 |
0.1939 |
11.9 |
18.3 |
Экстремальные значения параметров a, c, g, bбыли найдены сначала из условий минимума полной энергии. Экстремальные параметры a, c, g, bи энергия системы нами рассчитаны также из условий минимальности дисперсии 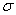 , поскольку локальная энергия, определяемая из (6) с использованием (3), имеет кулоновскую сингулярность. Значения полных энергий, найденных двумя вышесказанными способами для значений параметра анизотропии в интервале
, поскольку локальная энергия, определяемая из (6) с использованием (3), имеет кулоновскую сингулярность. Значения полных энергий, найденных двумя вышесказанными способами для значений параметра анизотропии в интервале 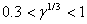 , отзличаются на малые проценты от общей энергии. На рисунке приведена зависимость величины минимизированной энергии для
, отзличаются на малые проценты от общей энергии. На рисунке приведена зависимость величины минимизированной энергии для 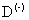 центра от параметра анизотропии, найденного первым вышеупомянутым способом. Для сравнения там же приведены результаты Кона и Латтинджера [2] для
центра от параметра анизотропии, найденного первым вышеупомянутым способом. Для сравнения там же приведены результаты Кона и Латтинджера [2] для 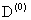 центра.
центра.
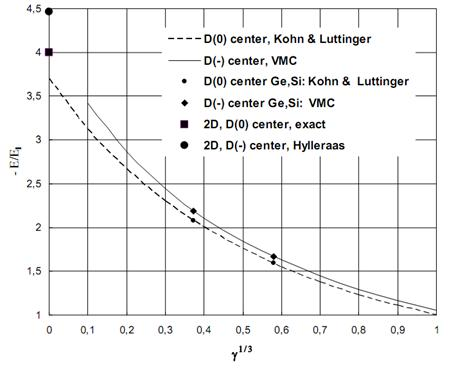
Рис. 1. Зависимость энергии 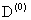 (штриховая линия) и
(штриховая линия) и 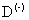 (сплошная линия) центров от параметра анизотропии
(сплошная линия) центров от параметра анизотропии 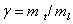
Согласно данному способу расчета, численные значения энергии связи одного электрона 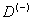 центра в Si и Ge в исходных единицах (2) соответственно равны 1.5806 meV и 0.4995 meV.
центра в Si и Ge в исходных единицах (2) соответственно равны 1.5806 meV и 0.4995 meV.
В данной работе вариационный метод МК применен к двухэлектронным центрам с анизотропией эффективных масс. Исходя из волновой функции 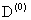 центра Кона и Латтинджера, нами для
центра Кона и Латтинджера, нами для 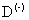 центра построена пробная волновая функция, в которой добавлен простой корреляционный множитель, использованный Хиллераасом.
центра построена пробная волновая функция, в которой добавлен простой корреляционный множитель, использованный Хиллераасом.
Обычно при моделировании изотропных объектов, таких как атомы, молекулы и атомные кластеры, сингулярность в локальной энергии исключаются с помощью функцией Жастрова. Если такое исключение затруднено, то необходимо проверить правильность полученных результатов. Сингулярность в локальной энергии в некоторых условиях (например, при понижении размерности или сильной анизотропии) могут порождать большую дисперсию при МК усреднении. Наши расчеты показали, что для полупроводников Si и Ge при усреднении их полной энергии возможная ошибка составляет около одного процента от общей энергии 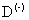 центра.
центра.
Обобщая вышесказанное, можно заключить, что проведенные нами исследования особенности МК моделирования этих систем позволяют моделировать другие малые системы, такие как экситоны, биэкситоны и трионы с анизотропией масс носителей в наноструктурах, и выявлять роли межэлектронных взаимодействий и границы (геометрию) наноструктуры.
Литература:
1. Б. М. Аскеров. Электронные явления переноса в полупроводниках. М.: Наука. 320 с. (1985)
2. W. Kohn, J. M. Luttinger, Phys. Rev., 98, 915 (1955)
3. R. A. Faulkner, Phys. Rev., 184, 713 (1969)
4. S. Huant, S. P. Najda, Phys. Rev. Lett., 65 (12), 1486 (1990)
5. А. С. Москаленко, И. Н. Яссиевич, ФТТ. 46, 8 (2004) 1465
6. D. M. Ceperely and B. J. Alder, Phys. Rev. Lett., 45, 566 (1980)
7. D. M. Ceperely and L. Mitas, Advances in Chemical Physics, Vol XCIII, edited by I. Prigogine and S. A. Rice (John Wiley and Sons 1996)
8. Quantum Monte Carlo Methods in Physics and Chemistry, Eds. M. P. Nightingle and C. J. Umrigar, Nato ASI Ser. C 525, (Kluwer, Dordrecht, 1999)
9. B. L. Hammond, J.W. A. Lester and P. J. Reynolds, Monte Carlo Methods in Ab Initio Quantum Chemistry (World Scientific, Singapore,1994)
10. М. Г. Веселов, Л. Н. Лабзовский. Теория атома. Строение электронных оболочек. М.: Наука. 328 с. (1986)
11. Ф. М. Морс и Г. Фешбах, Методы теоретической физики, т.2. ИЛ, М., (1959)
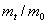
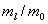
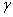
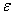
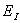 ,meV
,meV
