Библиографическое описание:
Ядгаров, У. Т. Распространение поперечных волн в бесконечно длинном цилиндрическом слое / У. Т. Ядгаров. — Текст : непосредственный // Молодой ученый. — 2016. — № 2 (106). — С. 277-280. — URL: https://moluch.ru/archive/106/25161/ (дата обращения: 24.04.2024).
В данной задаче рассматривается распространение поперечных волн в бесконечно длинном цилиндрическом слое, находящемся в упругой среде (рис.1). Основная цель исследования изучение существования фазовой скорости распространения волн от геометрических и физико-механических параметров системы. Основные уравнения теории упругости для таких задач сводятся к плоской задаче. В этом случае и осевое перемещение равно нулю [2]:
Рис. 1 Расчетная схема
,
a касательное перемещение U определяется как
(1)
где 
потенциал поперечных волн
Тогда волновое уравнение принимает следующий вид:
где
(i=1,2) (2)
-оператор дифференцирования
Решение волнового уравнения (2) для цилиндра 
и окружающей его среды 
записывается в виде:
где К0 — модифицированная функция Бесселя;
Н0(1) и Н0(2) — функции Ханкеля нулевого порядка первого и второго рода.
Для решения задачи ставятся различные условия при r = a1 и r = a2.
При r = a1: Rq1 = 0; r = a2; uq1 = uq2.
Компоненты вектора смещений в цилиндре и окружающей его среде представляются в виде:
По условию задачи при r =
a1: ur = 0, т. е.
0.
На контакте двух тел (r = a 2) ставится условие жесткого контакта, т. е.
uθ1= uθ2
,
также при r = a2: tRq1 = tRq2.
Здесь tRq1 = m1 gRq1; tRq2 = m2 gRq 2; В результате получим:
Для определения произвольных постоянных А1, В1 и С11 получим однородную систему алгебраических уравнений третьего порядка.
[C] {q}={0},
где (q} = {A1,B1,C11}T.
Для того, чтобы система однородных алгебраических уравнений имела нетривиальные решения, определитель алгебраических уравнений должен быть равен нулю. Их этих условий получим следующее дисперсионное уравнение:
, (3)
в случае К2z > К21
Для решения дисперсионного уравнения (3) составляем алгоритм на основе метода Мюллера [1], который определяет комплексные фазовые скорости. Заметим, что с увеличением толщины слоя первой и второй моды фазовая скорость уменьшается.
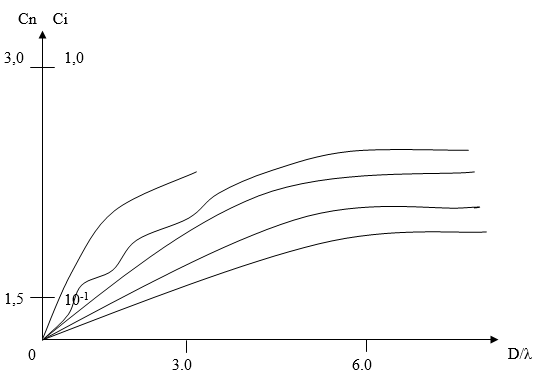
Рис. 2. Изменение скорости в зависимости от длины волн
Литература:
-
Сафаров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях. Ташкент; Фан. 1992 г. 250 с.
Основные термины (генерируются автоматически): волновое уравнение, дисперсионное уравнение.
Похожие статьи
В статье рассматривается электрическое поле, порождающее магнитное, которое оказывается переменным. Это переменное магнитное поле порождает электрическое. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле...
В статье рассматривается электрическое поле, порождающее магнитное, которое оказывается переменным. Это переменное магнитное поле порождает электрическое. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле...
Дисперсионное уравнение записывается в виде
Основные термины (генерируются автоматически): волновое число, фазовая скорость, двухслойный цилиндр, упругая среда, дисперсионное уравнение, напряжение, окружающая среда.
Дисперсионное уравнение записывается в виде
Основные термины (генерируются автоматически): волновое число, фазовая скорость, двухслойный цилиндр, упругая среда, дисперсионное уравнение, напряжение, окружающая среда.
Дисперсионное уравнение записывается в виде
Основные термины (генерируются автоматически): волновое число, фазовая скорость, упругая среда, двухслойный цилиндр, дисперсионное уравнение, напряжение, окружающая среда.
Дисперсионное уравнение записывается в виде
Основные термины (генерируются автоматически): волновое число, фазовая скорость, упругая среда, двухслойный цилиндр, дисперсионное уравнение, напряжение, окружающая среда.
Начальные данные формулируются так же, как и для классического волнового уравнения
Используя общее уравнение монохроматической волны , получим дисперсионное уравнение для (3) при
Начальные данные формулируются так же, как и для классического волнового уравнения
Используя общее уравнение монохроматической волны , получим дисперсионное уравнение для (3) при
(8). (9). Дисперсионное уравнение (8) описывает затухание альфвеновских волн в плазме с вязкой и омической диссипацией.
Значение критического числа Рэлея равно: (19). Отсюда видно, что критические числа Рэлея зависят не только от волновых чисел , но и от...
(8). (9). Дисперсионное уравнение (8) описывает затухание альфвеновских волн в плазме с вязкой и омической диссипацией.
Значение критического числа Рэлея равно: (19). Отсюда видно, что критические числа Рэлея зависят не только от волновых чисел , но и от...
В работе рассматривается распространение волн в двухслойном цилиндрическом теле с идеальной жидкостью. Задача решается в потенциалах перемещений. Дисперсионное уравнение решается методом Мюллера.
В работе рассматривается распространение волн в двухслойном цилиндрическом теле с идеальной жидкостью. Задача решается в потенциалах перемещений. Дисперсионное уравнение решается методом Мюллера.
Уравнение (3) для нахождения затухания нормальных волн, приравнивая к нулю мнимую часть.
Из рисунка видно что, с увеличением волновых чисел дисперсионные кривые приближаются к асимтотике.
Уравнение (3) для нахождения затухания нормальных волн, приравнивая к нулю мнимую часть.
Из рисунка видно что, с увеличением волновых чисел дисперсионные кривые приближаются к асимтотике.
Анализ уравнения, моделирующего волновые движения в тектоническом разломе. Горохов Александр Андреевич, аспирант; Черепанова Ирина Сергеевна, магистрант. Сибирский федеральный университет (г. Красноярск). Введение.
Анализ уравнения, моделирующего волновые движения в тектоническом разломе. Горохов Александр Андреевич, аспирант; Черепанова Ирина Сергеевна, магистрант. Сибирский федеральный университет (г. Красноярск). Введение.
Для вывода уравнений оболочки использован принцип возможных перемещений. Решения краевой задачи получены методом ортогональной прогонки Годунова. Были исследованы дисперсионные кривые в зависимости от различных геометрических параметров системы.
Для вывода уравнений оболочки использован принцип возможных перемещений. Решения краевой задачи получены методом ортогональной прогонки Годунова. Были исследованы дисперсионные кривые в зависимости от различных геометрических параметров системы.
