В [1] рассмотрен перенос вещества в среде с двойной пористостью, учитывающий обратимое и необратимое осаждение вещества в обеих зонах и равновесный обмен первого порядка между зонами. В каждой зоне, т. е. в трещинах и пористых блоках, происходит обратимое и необратимое осаждение (отложение) вещества с различными характеристиками, описываемые линейными уравнениями. Получено аналитическое решение задачи, которое использовано для описания результатов ранее проведенных экспериментов [2].
Используем аналогичную с [3] схему среды с двойной пористостью (Рис.1). В биконтинуальных средах, таких как трещиновато-пористые среды, необходимо использовать двухзонный подход, где в обеих зонах жидкость считается подвижной. В таких средах с двойной пористостью или двойной проницаемостью перенос вещества, как и движение жидкости происходит с различной интенсивностью, порою контрастной. Заметим что такой подход используется и для макроскопически неоднородных сред, где в обеих зонах может происходить конвективный перенос вещества.
Первая зона с индексом 1 в обозначениях имеет высокую проницаемость, а вторая зона — низкую. В каждой зоне есть по два участка, в каждой из которых происходит осаждение вещества с необратимой неравновесной кинетикой.
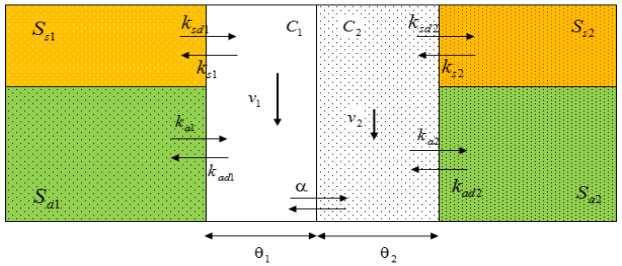
Рис.1. Схема переноса вещества в двухзонной среде
Здесь в отличие от [4] рассмотрим нелинейные уравнения кинетики.
Уравнения переноса вещества в одномерном случае записываем в виде [4]
,(1)
,
где 
— время, с, x-расстояние, м,
- коэффициент продольный дисперсии, 
— скорости движения жидкости, м/с,
,
- объемная концентрация вещества в жидкости,
и 
-концентрации отложенного вещества,
, 
- пористости зон, 
, 
- плотность среды, 
,
- коэффициент массообмена между зонами, 
.
Осаждение вещества в каждом из участков зон происходит обратимо в соответствии с кинетическими уравнениями
,(2)
,(3)
где 
,
- коэффициенты отложения вещества от жидкой фазы lна твердую фазу, 
, 
- коэффициенты отрыва вещества из твердой фазы и перехода в жидкость, 
,
Пусть в первоначально насыщенную чистой (без вещества) жидкостью среду с начального момента времени закачивается жидкость с постоянной концентрацией вещества 
. Рассмотрим такие периоды времени, где концентрационное поле не достигает правой границы среды, 
. При отмеченных допущениях начальные и граничные условия для задачи имеют вид
(4)
(5)
(6)
Задача (1) — (6) хотя и является линейной, получение аналитического решения является сложным, т. к. необходимо найти одновременно три поля в каждой из зон. Поэтому для решения задачи применяем метод конечных разностей. В рассматриваемой области 
введена равномерная по направлениям сетка
,
где I — достаточно большое целое число, выбираемое так, чтобы отрезок [
],
, перекрывал область расчетного изменения полей Ci, Sai и Ssi, h — шаг сетки по направлению х.
В открытой сеточной области
уравнения (1), (2), (3) аппроксимировались следующим образом
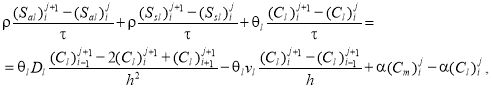(5)
,
,(6)
,(7)
где 
,
, 
— сеточные значения функций 
, 
, 
,
в точке 
.
Из явных сеточных уравнений (6), (7) определяем 
,
,(8)
,(9)
где
, 
,
, 
.
Сеточные уравнения (5) приводятся к виду
,(10)
где 
, 
, 
,
.
Устанавливается следующий порядок расчета решений. По (8), (9) определяются 
,
, затем решая систему линейных уравнений (10) методом прогонки — 
Поскольку
, схемы (8), (9) устойчивы, а для (10) условия устойчивости метода прогонки выполняются
.
В расчетах использованы следующие значения исходных параметров: 
, 
,
,
,
дисперсность
.
Некоторые характерные результаты показаны на рис. 2–4. Из рис.3 видно, что уменьшение показателя 
от единицы приводит к замедлению развития профилей концентрации (при неизменных остальных параметрах). Концентрации осажденного вещества при этом имеют опережающее развитие (рис.3,4). Другим словами, уменьшение показателя 
при прочих неизменных значениях остальных параметров приводит к интенсификации осаждения вещества в обоих участках зон. Как следствие этого в распределении концентраций вещества в подвижной жидкости обеих зон происходит отставание.
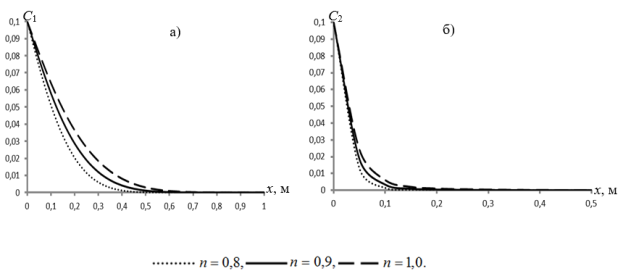
Рис.2. Профили концентраций Сl при
t=3600 c,
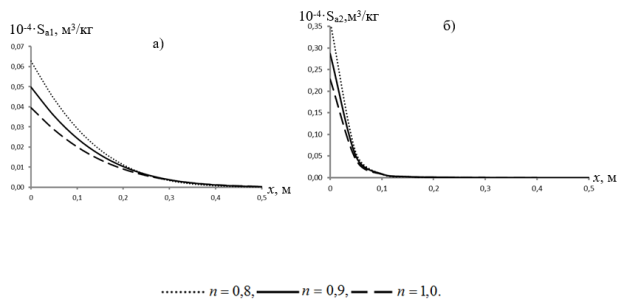
Рис. 3. Профили концентраций Sal при t=3600 c
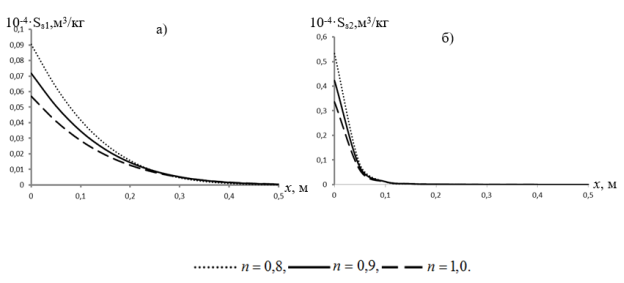
Рис. 4. Профили концентраций Ssl при
t=3600 c
Литература:
- Leij F. J., Bradford S. A. Combined physical and chemical nonequilibrium transport model: analytical solution, moments, and application to colloids // Journal of Contaminant Hydrology. 110. 2009. Pp. 87–99.
- Bradford S. A., Simunek J., Bettahar M., van Genuchten M. T., Yates S. R. Modeling colloid attachment, straining, and exclusion in saturated porous media // Environmental Science & Technology. 37. 2003. Pp. 2242–2250.
- Leij F. L., Bradford S. A. Colloid transport in dual-permeability media // Journal of Contaminant Hydrology. 150. 2013. Pp. 65–76.
- Feike J. L., Bradford S. A. Colloid transport in dual-permeability media // Journal of Contaminant Hydrology. 150. 2013.Pp.65−76.
