В 1967 году американские учёные К.С. Гарднер, Дж.М.Грин, М.Крускал и Р.Миура [1] открыли замечательное свойство уравнения Кортевега-де Фриза (КдФ). Они предложили нелинейную замену переменных в этом уравнении, после которой оно становится линейным и явно решается. В описании этой замены участвует формализм прямой и обратной задач рассеяния для оператора Штурма-Лиувилля, т.е. в нем существенно используется решение задачи о восстановлении потенциала оператора Штурма-Лиувилля на всей оси, по данным рассеяния. Этот метод получил название метода обратной задачи рассеяния. В работе [2] П.Лакс показал, универсальность метода обратной задачи рассеяния и обобщил уравнение КдФ, введя понятие высшего (общего) уравнения КдФ. Затем МОЗР был успешно применен и для многих других нелинейных эволюционных дифференциальных уравнений, таких как: нелинейное уравнение Шредингера, модифицированное уравнение Кортевега-де Фриза, уравнение sin-Гордон.
Рассмотрим линейную систему уравнений
(1)
на всей оси (
), с «быстроубывающим» потенциалом 
:
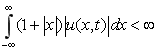.(2)
Здесь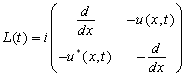 
, 
является комплексным сопряжением к 
.
Прямая и обратная задача рассеяния для оператора 
изучены в работах М.Г.Гасымова, Б.М.Левитана [3], В.Е.Захарова, А.Б.Шабата [4], И.С.Фролова [5], Л.П.Нижника, Фам Лой Ву [6], Л.А.Тахтаджяна, Л.Д.Фаддеева [7], А.Б.Хасанова [8] и др.
В данной работе рассматривается система уравнений
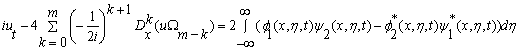, (3)
,(4)
, (5)
при начальном условии
,(6)
где 
определяется из следующих реккурентных соотношений
, 
, 
.
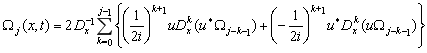Здесь начальная функция 
обладает следующими свойствами:
1) 
(7)
2) Оператор 
не имеет спектральных особенностей и в верхней полуплоскости комплексной плоскости имеет ровно N собственных значений 
с кратностями 
.
В рассматриваемой задаче вектор-функции 
и 
решения системы уравнений 
и 
соответственно, которые обладают следующими асимптотиками при 
, 
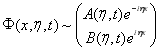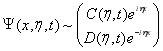,(8)
где
заданные непрерывные функции, удовлетворяющие условию:
при 
.(9)
Предполагается, что при всех 
(10)
Пусть функция 
обладает достаточной гладкостью, т.е. 
и достаточно быстро стремится к своим пределам при 
, так что
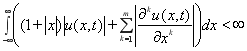.(11)
Основная цель данного работы – получить эволюции данных рассеяния несамосопряженного оператора 
с потенциалом являющимся решением уравнения (3).
Допустим, что решение 
задачи (3)-(11) существует. Рассмотрим систему уравнений
(12)
с потенциалом 
. Пусть вектор-функции 
и 
решения уравнений 
и 
соответственно с асимптотиками (8) при 
. С помощью решений Йоста 
и 
уравнений (12), определим вектор-функции
, (13)
.(14)
Здесь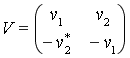 
и 
,
.
По определению, вектор-функции 
и 
аналитические функции от параметра 
в верхней полуплоскости 
. При любых действительных 
вектор-функции 
и 
имеют особенности в точке 
. Чтобы определить предельные значение вектор-функций 
и 
при 
, используем формулы Сохоцкого. В силу (13), (14) имеем
,(15)
.(16)
Здесь v.p. означает, что интеграл понимается в смысле главного значения.
Согласно (8) имеем
,
,
поэтому при 
:
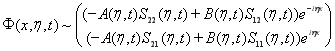,(17)
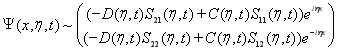.(18)
Нетрудно заметить, что справедливы равенства
.
Следовательно, 
и 
линейно зависимы с 
и 
соответственно, т.е. существуют такие 
и 
, что имеют место соотношения
,(19)
. (20)
По определению матрицы 
, из равенств (10) и асимптотик (8), (17) и (18), получим
,
где 
.
Введем следующее обозначение
.
На основании равенств (19), (20) вектор 
можно переписать в виде
.(21)
С другой стороны, из соотношений (15) и (16) имеем
.
Используя равенство 
получим
. (22)
Сравнивая равенства (21) и (22) имеем
(23)
,
следовательно
.
Заметим, что дифференциальное уравнение (23) справедливо при 
. Легко заметить, что при 
справедливо равенство
.(24)
Решая дифференциальное уравнение (24) получим
.
Отсюда следует, что нули 
функции 
, т.е. собственные значения оператора 
не зависят от 
.
Перейдем к нахождению эволюции нормировочной цепочки 
соответствующей 
кратным собственным значениям 
Заметим, что при 
справедливы равенства
, (25)
.(26)
Теперь определим функцию 
в виде
.
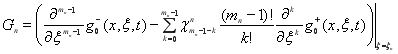В силу равенств (25) и (26) имеем
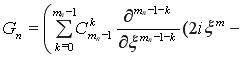
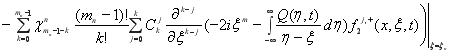. (27)
Равенство (27) можно переписать в виде
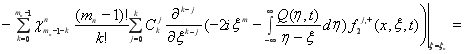
,(28)
где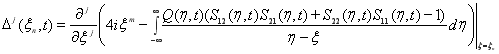 
,
Следовательно, согласно 
.
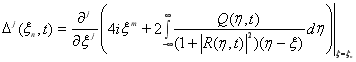С другой стороны, на основании равенств (13) и (14) имеем
.(29)
Сравнивая равенства (28) и (29), получим
, 
Таким образом доказана следующая
Теорема. Если функции 
являются решением задачи (3)-(11), то данные рассеяния несамосопряженного оператора 
с потенциалом 
меняются по 
следующим образом
,
, 
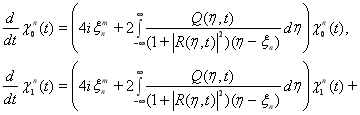
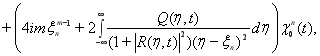
Полученные равенства полностью определяют эволюцию данных рассеяния, что позволяет применить метод обратной задачи рассеяния для решения задачи (3)-(11).
Литература:
- Gardner C.S., Сreen I.M., Kruskal M.D., Miura R.M. Method for solving the Korteweg-de Vries equation // Phys. Rev. Lett. – USA, 1967. – v.19 – p. 1095-1097.
- Lax P.D. Integrals of nonlinear equations of evolution and solitary waves // Comm. Pure and Appl. Math. – USA, 1968. – v.21. – p. 467-490.
- Гасымов М.Г., Левитан Б.М. Обратная задача для системы Дирака // ДАН СССР. – Москва, 1966. – Т.167, № 5. – C. 967-970.
- Захаров В.Е., Шабат А.Б. Точная теория двумерной самофокусировки и одномерной автомодуляции волн в нелинейной среде // ЖЭТФ. – Москва, 1971. – Т.61. № 1. – C.118-134.
- Фролов И.С. Обратная задача рассеяния для системы Дирака на всей оси // ДАН СССР. – Москва, 1972. – Т.207, № 1. – С.44-47.
- Нижник Л.П., Фам Лой Ву. Обратная задача рассеяния на полуоси с несамосопряженной потенциальной матрицей // Укр. матем. журнал. – Киев, 1974. – Т.26, № 4. – С.469-486.
- Тахтаджян Л.А., Фаддеев Л.Д. Гамильтонов подход в теории солитонов.–/ М.:, Наука. 1986. – 528 с.
- Хасанов А.Б. Об обратной задаче теории рассеяния для системы двух несамосопряженных дифференциальных уравнений первого порядка // ДАН СССР – Москва, 1984. – Т.277, № 3. – C. 559-562.
- Хасанов А.Б., Рейимберганов A.A. Конечно плотные решения высшего нелинейного уравнения Шредингера с самосогласованным источником // Уфимский матем. журнал. – Уфа 2009, том 1. № 4. – С. 133-143.
