Как известно, некоторые актуальные задачи, в частности, задачи квантовой механики, статистической механики и гидродинамики сводятся к исследованию спектральных свойств модели Фридрихса [1–3]. Пороговые резонансы для семейства модели Фридрихса с одномерным возмущением, которые ассоциированы с системой двух частиц на решетке изучены в работах [4,5], a для двухчастичного дискретного оператора Шредингера изучены в работах [6–8]. Поэтому изучение пороговых резонансов для модели Фридрихса играет важную роль в современной математической физике.
В настоящей работе рассматривается модель Фридрихса 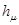 ,
, 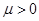 , в случае функции специального вида
, в случае функции специального вида  , являющейся параметром этого оператора. Показывается, что эта функция имеет невырожденный минимум в нескольких различных точках трехмерного тора
, являющейся параметром этого оператора. Показывается, что эта функция имеет невырожденный минимум в нескольких различных точках трехмерного тора 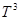 . Найдены необходимые и достаточные условия для того, чтобы, оператор
. Найдены необходимые и достаточные условия для того, чтобы, оператор 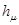 имел резонанс с нулевой энергией в зависимости от точки минимума функции
имел резонанс с нулевой энергией в зависимости от точки минимума функции  . При этом нуль является нижней гранью существенного спектра оператора
. При этом нуль является нижней гранью существенного спектра оператора 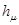 .
.
Пусть 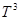 - трехмерный тор, т. е. куб
- трехмерный тор, т. е. куб 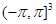 — с соответствующим отождествлением противоположных граней. Всюду в работе
— с соответствующим отождествлением противоположных граней. Всюду в работе 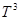 рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в
рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в 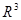 по модулю
по модулю 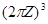 , где
, где 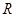 и
и 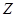 - множество вещественных и целых чисел, соответственно.
- множество вещественных и целых чисел, соответственно.
Пусть 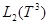 — гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на
— гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 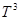 .
.
Рассмотрим модель Фридрихса 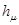 ,
, 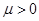 , действующий в
, действующий в 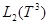 как
как 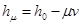 , где операторы
, где операторы 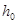 и
и 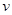 определяются по правилам:
определяются по правилам:
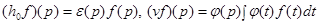 .
.
Здесь 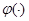 -вещественнозначная четная дважды непрерывно дифференцируемая функция на
-вещественнозначная четная дважды непрерывно дифференцируемая функция на 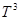 , а функция
, а функция  определена по формулам
определена по формулам
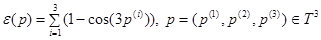 .
.
Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования. Очевидно, что при таких предположениях оператор 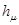 ограничен и самосопряжён в
ограничен и самосопряжён в 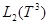 .
.
Обозначим через 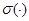 ,
, 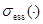 и
и 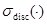 , соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
, соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Оператор возмущения 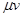 оператора
оператора 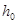 является самосопряженным одномерным оператором. Следовательно, из известной теоремы Г. Вейля [9] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора
является самосопряженным одномерным оператором. Следовательно, из известной теоремы Г. Вейля [9] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора 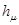 совпадает с существенным спектром оператора
совпадает с существенным спектром оператора 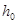 . Известно, что
. Известно, что 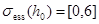 . Из последних фактов следует, что
. Из последних фактов следует, что 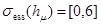 .
.
Определим регулярную в 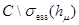 функцию (детерминант Фредгольма, ассоциированный с оператором
функцию (детерминант Фредгольма, ассоциированный с оператором 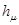 )
)
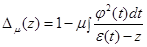 .
.
Теперь установим связь между собственными значениями оператора 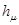 и нулями функции
и нулями функции 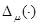 .
.
Лемма 1. Оператор 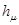 имеет собственное значение
имеет собственное значение 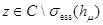 тогда и только тогда, когда
тогда и только тогда, когда 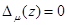 .
.
Из леммы 1 вытекает, что 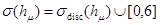 , где
, где
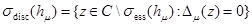 .
.
Рассмотрим точки 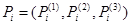 из
из 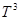 , для которых
, для которых
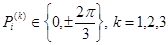 ,
,
причем 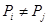 при
при 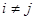 . Ясно, что число таких точек равно 27.
. Ясно, что число таких точек равно 27.
Легко проверяется, что функция  имеет невырожденный минимум в точках
имеет невырожденный минимум в точках 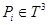 ,
, 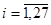 . Функция
. Функция 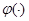 является непрерывной на
является непрерывной на 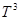 , поэтому существует конечный интеграл
, поэтому существует конечный интеграл
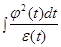 .
.
Полагая
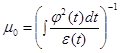
получим, что 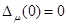 тогда и только тогда, когда
тогда и только тогда, когда 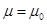 .
.
Пусть 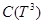 (соот.
(соот. 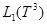 ) — банахово пространство непрерывных (соот. интегрируемых) функций, определенных на
) — банахово пространство непрерывных (соот. интегрируемых) функций, определенных на 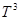 .
.
Определение 1. Говорят, что оператор 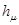 имеет резонанс с нулевой энергией, если число
имеет резонанс с нулевой энергией, если число 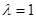 является собственным значением интегрального оператора
является собственным значением интегрального оператора
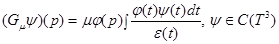
и по крайней мере одна (с точностью до константы) соответствующая собственная функция 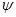 удовлетворяет условию
удовлетворяет условию 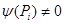 при некотором
при некотором 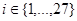 .
.
Следующая теорема о необходимых и достаточных условиях для того чтобы, оператор 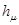 имел резонанс с нулевой энергией.
имел резонанс с нулевой энергией.
Теорема 1. Оператор 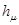 имеет резонанс с нулевой энергией тогда и только тогда, когда
имеет резонанс с нулевой энергией тогда и только тогда, когда 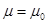 и
и 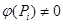 при некотором
при некотором 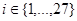 .
.
Доказательство. Необходимость. Пусть оператор 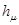 имеет резонанс с нулевой энергией. Тогда по определению 1 уравнение
имеет резонанс с нулевой энергией. Тогда по определению 1 уравнение
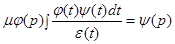 (1)
(1)
имеет нетривиальное решение 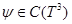 , удовлетворяющее условию
, удовлетворяющее условию 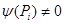 при некотором
при некотором 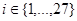 . Видно, что это решение равно (с точностью до константы) функции
. Видно, что это решение равно (с точностью до константы) функции 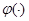 и следовательно,
и следовательно, 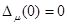 , т. е.
, т. е. 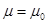 .
.
Достаточность. Пусть 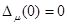 и
и 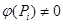 при некотором
при некотором 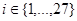 . Тогда функция
. Тогда функция 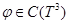 является решением уравнения (1), и следовательно, по определению 1 оператор
является решением уравнения (1), и следовательно, по определению 1 оператор 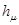 имеет резонанс с нулевой энергией. Теорема 1 доказано.
имеет резонанс с нулевой энергией. Теорема 1 доказано.
Теперь докажем, что если оператор 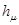 имеет резонанс с нулевой энергией, то функция
имеет резонанс с нулевой энергией, то функция 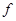 , определенная по формуле
, определенная по формуле
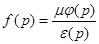 (2)
(2)
удовлетворяет уравнению 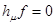 и
и 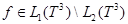 .
.
Действительно, если при некотором 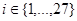 верно
верно 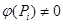 , то из непрерывности функции
, то из непрерывности функции 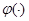 следует, что существуют числа
следует, что существуют числа 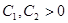 и
и 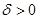 такие, что
такие, что
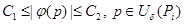 , (3)
, (3)
где
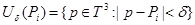 .
.
Кроме того из определения функции  для некоторых
для некоторых 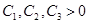 и
и 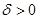 получим, что
получим, что
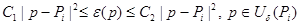 , (4)
, (4)
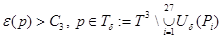 . (5)
. (5)
Имеет место равенство
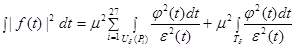 .
.
Если при некотором 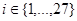 верно
верно 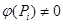 , то используя неравенства (3)-(5) получим, что
, то используя неравенства (3)-(5) получим, что
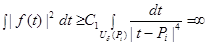 ,
,
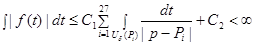 .
.
Таким образом если при некотором 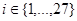 верно
верно 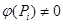 , то
, то 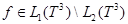 . Это и означает, что в определении 1 требование наличия собственного значения
. Это и означает, что в определении 1 требование наличия собственного значения 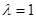 оператора
оператора 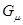 соответствует существованию решения уравнения
соответствует существованию решения уравнения 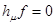 , а из условия
, а из условия 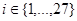 верно
верно 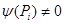 следует, что решение
следует, что решение 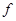 этого уравнения не принадлежит пространству
этого уравнения не принадлежит пространству 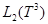 .
.
Из доказательства теоремы 1 видно, что если оператор 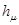 имеет резонанс с нулевой энергией, тогда решение уравнения
имеет резонанс с нулевой энергией, тогда решение уравнения 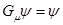 равно (с точностью до константы) функции
равно (с точностью до константы) функции 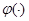 .
.
Отметим, что теорема 1 играет важную роль [10] при изучении конечности или бесконечности дискретного спектра соответствующего трехчастичного модельного оператора в зависимости от точки минимума функции  .
.
Литература:
1. Фаддеев Л. Д. О модели Фридрихса в теории возмущений непрерывного спектра. Труды Мат. Инс-та АН СССР, 73 (1964), С. 292–313.
2. Минлос Р. А., Синай Я. Г. Исследование спектров стохастических операторов, возникающих в решетчатых моделях газа. Теор. и матем. физ. 2:2 (1979), С. 230–243.
3. Дынкин Е. М., Набако С. Н., Яковлев С. И. Граница конечности сингулярного спектра в самосопряженной модели Фридрихса. Алгебра и анализ. 3:2 (1991), С. 77–90.
4. Albeverio S., Lakaev S. N., Muminov Z. I. The threshold effects for a family of Friedrichs models under rank one perturbations. J. Math. Anal. Appl. 330 (2007), P. 1152–1168.
5. Albeverio S., Lakaev S. N., Djumanova R. Kh. The Essential and Discrete Spectrum of a Model Operator Associated to a System of Three Identical Quantum Particles. Rep. Math. Phys. 63:3 (2009), P. 359–380.
6. Albeverio S., Lakaev S. N., Makarov K. A., Muminov Z. I. The threshold effects for the two-particle Hamiltonians in lattice. Comm. Math. Phys. 262 (2006), P. 91–115.
7. Albeverio S., Lakaev S. N., Muminov Z. I. Schroedinger operators on lattices. The Efimov effect and discrete spectrum asymptotics. Ann. Henri Poincare. 5 (2004), P. 743–772.
8. Абдуллаев Ж. И., Лакаев С. Н. Асимптотика дискретного спектра разностного трехчастичного оператора Шредингера на решетке. Теор. и мат. физ., 136:2 (2003), С. 231–245.
9. Рид М., Саймон Б. Методы современной математической физики. Т. 4, Анализ операторов. — М., Мир, 1982.
10. Расулов Т. Х. Асимптотика дискретного спектра одного модельного оператора, ассоциированного с системой трех частиц на решетке. Теор. и матем. физ. 163:1 (2010), С. 34–44.

