Настоящая статья является продолжением работы [1], в которой рассмотрено семейство обобщенных моделей Фридрихса. Там обсужден случай, когда параметр функции этой модели имеет специальный вид и невырожденный минимум в 
, 
, различных точках шестимерного тора. В данной работе рассматривается обобщенная модель Фридрихса 
, 
. Изучено число и местоположение собственных значений оператора в зависимости от параметра взаимодействия 
. Пусть 
— одномерное комплексное пространство и 
- гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на 
, 
. Обозначим через 
прямую сумму пространств 
и 
, т. е. 
. Гильбертово пространство называется двухчастичным обрезанным подпространством Фоковского пространства.
Рассмотрим обобщенную модель Фридрихса , действующую в гильбертовом пространстве и задающуюся как операторная матрица
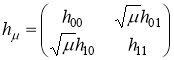, (1)
где операторы 
, 
и 
, 
определяются по формулам
, 
, 
, 
;
, 
, 
, 
.
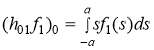Здесь 
и 
- вещественные числа. Легко можно проверить, что в этих предположениях оператор , определенный по формуле (1), и действующий в гильбертовом пространстве 
, является ограниченным и самосопряженным.
Оператор возмущения 
, 
оператора 
, является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г.Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора , совпадает с существенным спектром оператора 
. Известно, что 
, поэтому независимо от параметра взаимодействия 
имеет место равенство 
.
С целью изучения дискретного спектра оператора , определим регулярную в 
следующую функцию (определитель Фредгольма, ассоциированный с оператором ):
.
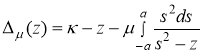Следующая лемма устанавливает связь между собственными значениями оператора
и нулями функции 
.
Лемма 1. При каждом фиксированном число 
является собственным значением оператора тогда и только тогда, когда 
.
Из определения функции следует, что она монотонно убывает на промежутках 
и 
. Следовательно, имеют место следующие утверждения.
Лемма 2. Оператор имеет единственное собственное значение, лежащее на 
тогда и только тогда, когда 
.
Лемма 3. Оператор имеет единственное собственное значение, лежащее на 
тогда и только тогда, когда 
.
Далее исследуем поведение функции в точках 
и 
. Очевидно, что
, 
.
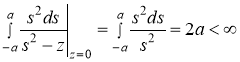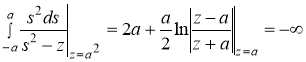Из теоремы о предельном переходе под знаком интеграла Лебега следует, что
, 
.
Основным результатом настоящей работы является следующая теорема.
Теорема 1. При каждом фиксированном оператор имеет не менее одного и не более двух собственных значений, лежащих вне существенного спектра. Кроме, того
1)для любого
оператор имеет единственное собственное значение, лежащее на промежутке ;
2)существование собственного значения оператора на промежутке зависит от значения параметра взаимодействия ;
2.1) если 
, то оператор не имеет отрицательных собственных значений;
2.2) если 
, то оператор имеет единственное отрицательное собственное значение;
3) если 
, то число 
является единственным собственным значением оператора 
, расположение которого зависит от 
.
Литература:
1. Р. Р. Гадаев, У. А. Джонизоков. О семействе обобщенных моделей Фридрихса. Молодой учёный, –2016, — № 13 (117). — С. 5–7.
