Как известно, что некоторые актуальные задачи, в частности, задачи квантовой механики, статистической механики и гидродинамики сводятся к исследованию спектральных свойств модели Фридрихса [1,2]. Поэтому изучение собственных значений модели Фридрихса играет важную роль в современной математической физике.
Впервые в 1937 г. в работе [3] Фpидpихс предложил рассмотреть в качестве пpостой модели теоpии возмущений непpеpывного спектpа следующий оператор:
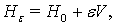
где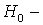 
оператор умножения на независимую переменную, действующий в гильбертовом пространстве функций, квадратично-интегрируемых на отрезке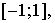 
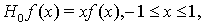
а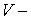 
ограниченный интегральный оператор
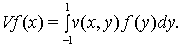
Невозмущенный опеpатоp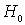 
имеет абсолютно непрерывный спектр, расположенный на отpезке 
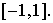Пpедполагая, что ядpо 
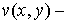гёльдеровски непpеpывная функция своих пеpеменных, удовлетвоpяющая условию
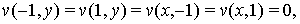
Фpидpихс доказал, что пpи всех достаточно малых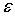 
, 
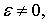опеpатоpы 
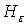и 
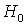унитаpно эквивалентны.
Эта модель в дальнейшем называлась моделью теории возмущений непрерывного спектра, так как непрерывный (существенный) спектр самосопряженного оператора не изменяется при компактном возмущении.
Фpидpихс в pаботе [4] пpедложил следующим обpазом обобщить свою модель: во-пеpвых, pассматривать вместо отpезка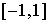 
пpоизвольный (конечный или бесконечный) интеpвал 
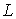на вещественной оси, во-втоpых, pассматpивать функции 
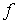со значениями в некотоpом абстрактном гильбеpтовом пpостpанстве 
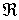. В этом случае для любых 
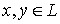ядро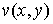 
есть ограниченный оператор в том же гильбеpтовом пpостpанстве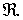 
В случае бесконечного интервала 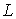накладывая на это ядpо дополнительное тpебование относительно его убывания на бесконечности, Фpидpихс пеpенес сфоpмулиpованный выше pезультат на рассматриваемый более общий случай. Предложенное обобщение значительно расширяет область применимости развитой теории.
В настоящей работе рассматривается ограниченный самосопряженный модель Фридрихса в одномерном случае. Найдены условия существование собственных значений этой модели.
Пусть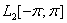 
— гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 
.
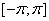В гильбертовом пространстве 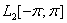рассмотрим модель Фридрихса 
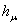действующий по формуле
,
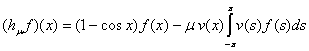где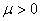 
и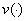 
вещественно-аналитическая функция на .
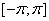В этих предположениях оператор 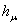является ограниченным и самосопряженным в гильбертовом пространстве .
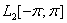Этот модель ассоциировано с системой двух одинаковых частиц на одномерной решетке и полученные результаты играют важный роль при оценке нижнего граня существенного спектра соответствующего модельного оператора, ассоциированного с системой трех одинаковых частиц на одномерной решетке.
Обозначим через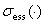 
и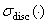 
соответственно существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Оператор возмущения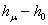 
оператора 
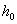является самосопряженным одномерным оператором. Следовательно, из известной теоремы Г. Вейля [5] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора 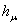совпадает с существенным спектром оператора 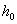. Известно, что
.
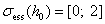Из последних фактов следует, что
.
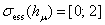При каждом фиксированном 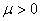определим регулярную в 
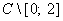функции
.
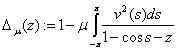Функция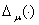 
называется детерминантом Фредгольма, ассоциированный с оператором .
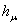Следующая лемма устанавливает связь между собственными значениями оператора 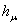и нулями функции .
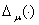Лемма 1. При каждом фиксированном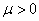 
число 
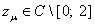является собственным значением оператора 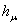тогда и только тогда, когда 
.
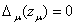Из леммы 1 вытекает, что для дискретного спектра оператора 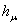имеет место равенство
.
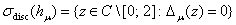Теперь исследуем дискретный спектр оператора .
Теорема 1. Если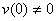 
, то для любого 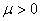оператор 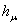имеет единственный простой отрицательной собственной значений 
.
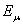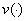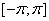Доказательство. Пусть . Тогда из непрерывности функции на следует, что существуют числа 
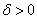и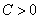 
такие, что 
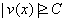при всех 
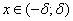. Из разложения
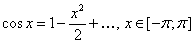
следует, что существуют числа 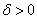и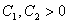 
такие, что
.
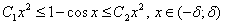Следовательно,
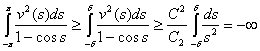
и поэтому
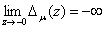
при всех .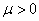
Так как для любого 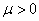функция 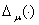является непрерывной и монотонно убывающий в 
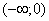, из равенство
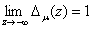(1)
вытекает, что для любого 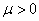функция 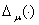имеет единственный ноль 
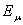, лежащее в 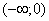. В силу леммы 1 число 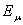является собственным значением оператора . Теорема 1 доказана.
Отметим, что если , то из вещественно-аналитичности функции 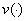на 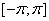следует, что существуют положительные числа 
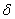и 
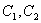такие, что имеет место неравенства
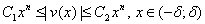(2)
для некоторого натурального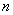 
. Используя неравенства (2) получим положительность и конечность интеграла
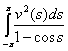
Положим
.
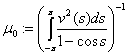Теорема 2. Пусть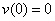 
.
а) Если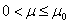 
, то оператор не имеет собственных значений;
б) Если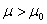 
, то оператор имеет единственное отрицательное простое собственное значение .
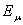Доказательство. Сначала заметим, что если при всех 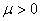и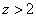 
имеет место неравенство 
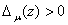. Поэтому в силу леммы 1 для любого 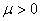оператор не имеет собственных значений, лежащих на 
.
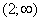а) Пусть 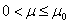. Для любого 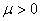функция 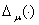монотонно убывает в полуоси 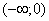. Поэтому
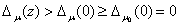
при всех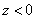 
и 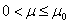, т. е. 
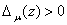при всех 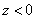и 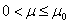. Следовательно, в силу леммы 1 для любого 
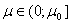оператор не имеет собственных значений.
б) Пусть теперь 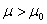. Тогда как выше для любого 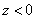имеем
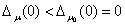. (3)
Так как для любого 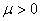функция 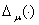является непрерывной и монотонно убывающий в 
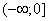в силу неравенства (3) для любого 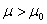существует единственный точка 
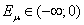такое, что 
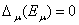. В силу леммы 1 для любого 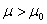точка 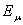является единственным простым собственным значением оператора . Теорема 2 доказана.
Литература:
1. Л. Д. Фаддеев. О модели Фридрихса в теории возмущений непрерывного спектра // Труды Математического Института АН СССР, 1964, Т. 73, С. 292–313.
2. Р. А. Минлос, Я. Г. Синай. Исследование спектров стохастических операторов, возникающих в решетчатых моделях газа // Теоретическая и математическая физика, 1979, Т. 2, № 2, С. 230–243.
3. Friedrichs K. O. Uber die Spectralzerlegung einee Integral operators // Math. Ann. 1938, V. 115, No. 2, P. 249–272.
4. Friedrichs K. O. On the perturbation of continuous spectra // Comm. Pure. Appl. Math. 1948, V. 1, No. 4. P. 361–406.
5. М. Рид, Б. Саймон. Методы современной математической физики // Т. 4, Анализ операторов, М.: Мир, 1982.
