В рамках проблемы нескольких тел на непрерывном пространстве и на решетке исследовано большое число задач о существовании собственных значений для систем квазичастиц, число которых сохраняется [1]. Однако имеются в определенном смысле более актуальные и интересные задачи, возникающие в теории твердого тела [2], статистической физике [3], теории квантового поля [4] и теории химических реакций [5], в которых число квазичастиц не сохраняется.
В настоящей работе рассматривается семейство обобщенной модели Фридрихса 
,
,
, действующей в двухчастичном обрезанном подпространстве фоковского пространства. Описано множество собственных значений лежащих ниже существенного спектра оператора 
.
Пустъ 
-трехмерный куб с соответствующим отождествлением противоположных граней, 
— гилъбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 
, 
-одномерное комплексное пространство.
Обозначим 
, 
, 
.
Определение 1. Гилъбертово пространство H называется двухчастичным обрезанным подпространством Фоковского пространства.
Рассмотрим семейство ограниченных и самосопряженных операторов 
, 
, 
(семейство обобщенных моделей Фридрихса), действующих в гилъбертовом пространстве 
и задающихся формулой
,
,
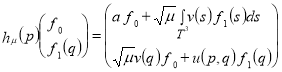(1)
Где 
и 
— вещественные положительные числа, 
-вещественно-непрерывная (отличная от нуля) функция на 
, а функция 
определяется равенством:
,
, 
.
Оператор возмущения
, 
оператора 
, 
является самосопряженным оператором ранга 2. Следовательно, из известной теоремы Г.Вейля о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора 
совпадает с существенным спектром оператора 
, 
. Известно, что
,
где числа 
и 
определяются равенствами:
, 
.
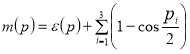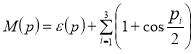Из последних двух фактов следует, что
.
Видно, что существенный спектр оператора 
не зависит от 
. В частности
.
Замечание 2. Отметим, что функция 
записывается в виде
, 
.
Следовательно, для любого 
функция 
имеет единственный невырожденный минимум в точке 
.
Следующая теорема описывает число собственных значений оператора
.
Теорема 1. Для любого 
оператор имеет не более чем по одному простых собственных значений лежащихлевее и правее существенного спектра.
Положим:
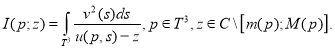
Для любых 
и 
имеет место 
. Так как функция 
имеет единственный невырожденный минимум в точке 
и 
непрерывная функция на 
, в силу теоремы Лебега о предельном переходе под знаком интеграла имеем, что существует конечный интеграл
.
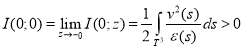Обозначим 
Следующая теорема описывает расположение собственных значений оператора .
Теорема 2.
1)Для любых 
и оператор не имеет собственных значений, лежащих ниже существенного спектра;
2)Для любого ненулевого оператор 
имеет единственное собственное значение 
лежащее на 
;
3)Для любых
и оператор имеет единственное собственное значение 
Более того
и 
В силу теоремы 2 можно сформулировать аналогичную теоремы о собственном значении оператора лежащих правее его существенного спектра.
Заметим, что теорема 2 играет важную роль при изучени структуры существенного спектра оператора
действующего в гильбертовом пространстве
Здесь под знаком интеграла стоят одинаковые слои.
Литература:
- Ю. А. Изюмов, М. В. Медведев. Магнитный полярон в ферромагнитном кристалле. ЖЭТФ. 1970, вып. 2, № 8, с. 553–560.
- А. Т. Mogilner. Hamiltonians of solid state physics at few particle discrete Schroedinerger operators: problems and results. Advances in Sov. Math. 5 (1991), 139–194.
- V. A. Malishev and R. A. Minlos. Linear infinite-particle operators. Translations of Math. Monagraphs. Amer. Math. Soc. Trasl. 177 (1996), № 2, 159–193.
- K. O. Friedrichs. On the perturbation of continuous spectra. Comm. Appl. Math. 1 (1948), 361–406.
- V. Bach, J. Froehlich, I. M. Sigal. Mathematical theory of non-relavistic matter and radiation. Lett. Math. Phys. 34 (1995), 183–201.
