Изображение геометрического тела в изометрической проекции, например правильной шестигранной призмы, выполняют в такой последовательности (рис. 1):
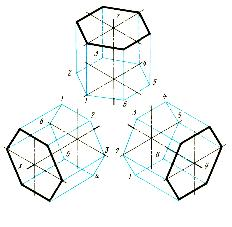
Рис. 1.
Если основание призмы — правильный многоугольник (например, шестиугольник), то построение вершин основания по координатам можно упростить, проведя одну из осей координат через центр основания. На рис. 1 оси х, у и z проведены через центры правильных шестиугольников призмы.
Построив изометрическую проекцию основания призмы, из вершин шестиугольника основания проводим прямые, параллельные соответственно осям х, у или z (для каждой из рассматриваемых на рис. 1 призм) [1]. На этих прямых от вершин основания отложим высоту призмы и получим точки 1, 2, 3, 4, 5, 6 вершин другого основания призмы. Соединив эти точки прямыми, получим изометрическую проекцию призмы. В заключение устанавливаем видимые и невидимые линии; невидимые линии надо проводить штриховыми линиями.
Построение изометрической проекции правильной пирамиды выполняют в той же последовательности, т. е. строят основание и высоту, а затем проводят ребра. Если пирамида усеченная, строят ее второе основание.
На рис. 2 показано построение изометрической проекции плоской детали криволинейного очертания по комплексному чертежу [2]. Деталь расположена параллельно фронтальной плоскости проекций. На фронтальной проекции комплексного чертежа намечают ряд точек и строят их на изометрической проекции (рис. 2-в). На рис. 2-б и в показано построение точки 14.
Через построенные точки контура кулачка проводят по лекалу кривую линию.
Параллельно оси у от найденных точек проводят прямые линии, на которых откладывают отрезки, равные А (толщине детали). Соединяя новые точки, получают контур другой плоскости детали, который также обводят по лекалу.
Аналогично строят изометрическую проекцию кулачка, расположенного параллельно горизонтальной плоскости проекций.
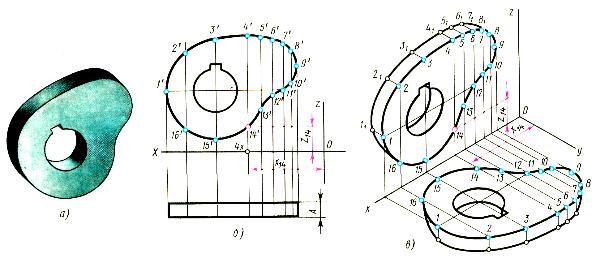
Рис. 2.
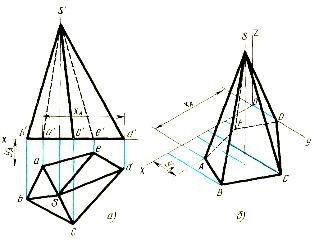
Рис. 3.
На рис. 3 показано построение изометрической проекции неправильной пятиугольной пирамиды по ее комплексному чертежу. Определяем координаты всех точек основания пирамиды, затем по координатам х и у строим изометрическую проекцию пяти точек — вершин основания пирамиды. Так, например, изометрическая проекция точки А получается следующим образом.
По оси х от намеченной точки О откладываем координату XA=a'd. Из конца ее проводим прямую, параллельную оси у, на которой откладываем вторую координату этой точки уА=а'а.
Далее строят по координатам высоту пирамиды и получают точку S — вершину пирамиды. Соединяя точку S с точками А, В, С, D и Е, получают изометрическую проекцию пирамиды.
Последовательность построения изометрической проекции детали по данному комплексному чертежу показана на рис. 4.
Деталь мысленно разделяют на отдельные простейшие геометрические элементы, в данном случае на призматические элементы (рис. 4, б).
Находят центры окружностей (рис. 4-в). Затем удаляют лишние построения, контур изображения обводят сплошной основной линией (рис. 4-г).
Для выявления внутренней формы предмета применяют вырез одной четверти детали. Разрезы в аксонометрических проекциях можно строить двумя способами.
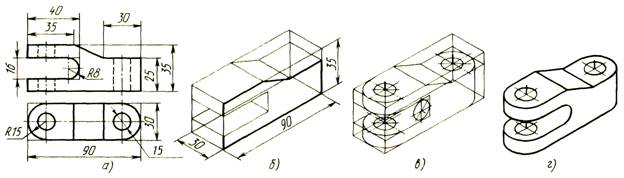
Рис. 4
Первый способ. Вначале строят в тонких линиях аксонометрическую проекцию (рис. 5-а). Затем выполняют вырез, направляя две секущие плоскости по осям х и у (рис. 5-б). Удаляют часть изображаемого предмета (рис. 5-в), после чего штрихуют сечения и обводят изображение сплошными толстыми линиями (рис. 5-г). Второй способ построения разреза при изображении деталей в аксонометрической проекции показан на рис. 6. Сначала строят аксонометрические проекции фигур сечения, а затем дочерчивают части изображения предмета, расположенные за секущими плоскостями (рис. 6-б).
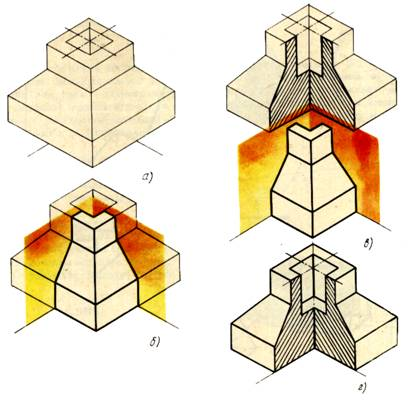
Рис. 5
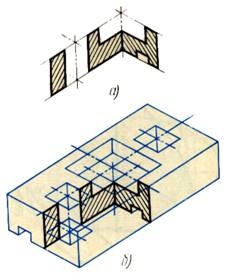
Рис. 6
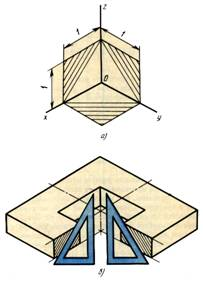
Рис. 7
Второй способ упрощает построение, освобождает чертеж от лишних линий.
Линии штриховки сечений в аксонометрических проекциях наносят, как показано на рис. 7, параллельно диагоналям проекций квадратов, которые лежат в плоскостях проекций и стороны которых параллельны аксонометрическим осям. Штриховку сечений в изометрической проекции удобно выполнять треугольником с углами 30 и 60° (рис. 7-б).
Литература:
1. Вышнепольский И. С. Техническое черчение. — М.: Высшая школа, 1981. — 216 с.
2. Боголюбов С. К. Черчение. — М.: Машиностроение, 1989. — 336 с.

