В школьном курсе математики в полной мере изучаются два специальных вида последовательностей — арифметическая и геометрическая прогрессии, однако последовательности, обобщающие их, т. е. сочетающие их свойства и признаки, в явном виде не рассматриваются.
Известно, что ряд различных типов последовательностей по природе своей являются рекуррентными, или возвратными, в том смысле, что каждый следующий член последовательности по определенному правилу выражается через некоторое фиксированное число предыдущих. К таким последовательностям относятся арифметическая и геометрическая прогрессии, последовательность Фибоначчи и др. [1]
В данной статье представлены итоги исследования рекуррентной последовательности 
, заданной по правилу 
, где числа 
и 
называем соответственно знаменателем и разностью этой последовательности, а саму последовательность — арифметико-геометрической прогрессией.
Актуальность исследования обусловлена тем, что в настоящее время эта проблема стала особенно значима для науки и практики. Этим вопросом занимаются многие теоретики и исследователи. Изучению прогрессий посвящены статьи в периодических изданиях и монографии многих ученых. Как правило, информация, посвященная данной проблеме, изложенная в учебной литературе, имеет общий характер, а в современных монографиях по этой теме анализируются более узкие вопросы проблемы.
Высокая значимость и недостаточная теоретическая разработанность проблемы изучения арифметико-геометрической прогрессии определяют несомненную новизну данного исследования.
Определение 1. [2] Арифметико-геометрическая прогрессия задается следующим рекуррентным соотношением:
, (1)
где 
и — постоянные, называемые соответственно знаменателем и разностью арифметико-геометрической прогрессии.
Замечание 1. При q=1 и d=0 получим стационарную последовательность 
.
В случае
и в (1), получим арифметическую прогрессию 
, а при 
и 
, — геометрическую прогрессию: 
.
Вышеуказанное замечание отражается в названии рассматриваемой последовательности: арифметико-геометрическая прогрессия.
Рассмотрим примеры арифметико-геометрических прогрессий.
1) 
;
2) 
.
Указание явных формул для нахождения общего члена последовательности, а также для суммы ее первых n членов являются основными задачами о последовательностях.
Арифметико-геометрическая прогрессия является обобщением арифметической и геометрической прогрессий. А значит, по аналогии можно вывести формулы для нахождения общего члена арифметико-геометрической прогрессии, а также для суммы ее первых n членов, и установить характеристическое свойство данного типа последовательности, а также ряд других важных свойств.
В ходе исследования были получены конкретные результаты:
1. Выведена формула n-го члена последовательности: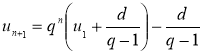 
.
Пусть в соотношении (1) 
. Прибавив к обеим частям равенства 
выражение 
, получим
.
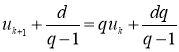
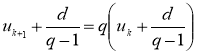Последнее соотношение является рекуррентным, поэтому можно записать аналогичные равенства для
:
, 
,…, 
.
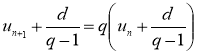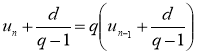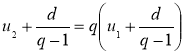Перемножив выписанные равенства, имеем:
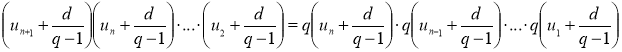
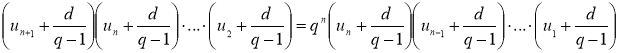
Разделив обе части последнего равенства на произведение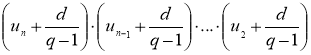 
, получим 
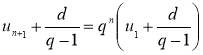, откуда 
.
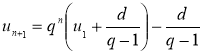Таким образом, получили формулу общего члена арифметико-геометрической прогрессии
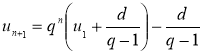. (2)
2. Доказано, что арифметико-геометрическая прогрессия сходится и ограничена только в случае, когда 
;
Из формулы общего члена арифметико-геометрической прогрессии следует, что
а) при 
арифметико-геометрическая прогрессия сходится к числу
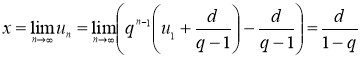, а значит, при эта последовательность ограничена.
б) при
арифметико-геометрическая прогрессия расходится и не ограничена.
3. Выведена формула суммы первых n членов арифметико-геометрической прогрессии: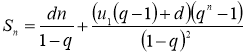 
. Также установлено, что сумма бесконечного числа членов последовательности не существует.
Рассмотрим n-ую частичную сумму 
арифметико-геометрической прогрессии .
Согласно соотношению (1), имеем:
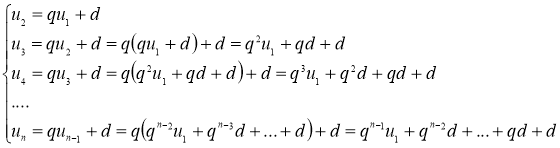
Тогда
. (3)
Умножив последнее равенство на знаменатель 
, получим
или 
(4)
Из равенства (3) вычтем равенство (4) и выполним преобразования.
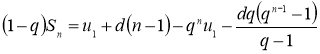
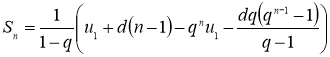
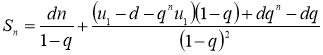
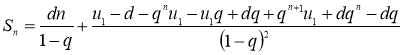
Преобразуя последнее равенство, получим формулу суммы 
первых n членов арифметико-геометрической прогрессии: 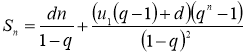. (5)
4. Доказано, что арифметико-геометрическая прогрессия является возвратной последовательностью второго порядка и задается возвратным уравнением 
; как следствия были получены характеристические свойства арифметической и геометрической прогрессий.
Действительно, будем утверждать, что при k=1 и при любом 
справедливо равенство 
. Осталось определить значения 
.
В силу соотношения (1) 
, тогда
.
Из равенства 
следует, что
,
,
, откуда уравняв коэффициенты, получим систему линейных уравнений с двумя переменными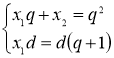 
, решением которой является 
.
Итак, верно равенство . Что и требовалось доказать.
5. Выведены формулы для нахождения разности 
и знаменателя 
арифметико-геометрической прогресси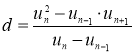и: 
и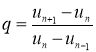 
.
6. Доказано характеристическое свойство арифметико-геометрической прогрессии : последовательность 
, где 
, является геометрической прогрессией с тем же знаменателем 
, то есть 
. (6)
Доказательство. Согласно формуле (2)
.
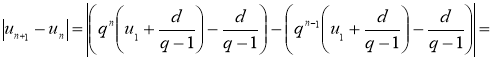
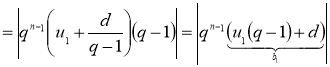Упростив правую часть равенства (6), получим:
.
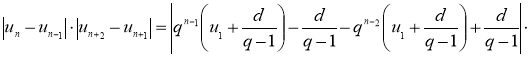
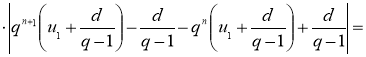
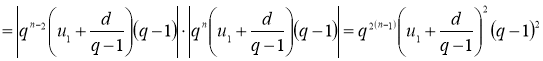Тогда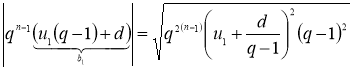 
.
Таким образом, доказано равенство (6), которое и является характеристическим свойством арифметико-геометрической прогрессии.
Все полученные результаты являются новыми. Данные результаты имеют научную и практическую ценность, в частности, они могут быть использованы при решении геометрических задач. [2]
В доступной нам литературе подобные исследования ранее не встречались, лишь некоторые свойства арифметико-геометрической прогрессии встречаются без доказательства.
Литература:
- Маркушевич А. И. Возвратные последовательности — М.: Наука, 1975. — 47 с.
- Суконник Я. Н. Арифметико-геометрическая прогрессия. Научно-популярный физико-математический журнал «Квант», № 1 1975г. — с.80
- Вавилов В. В., Красников П. М. Математические коллоквиумы. — М.: Школа им. А. Н. Колмогорова СУНЦ МГУ, 2006. — с. 60
