Изучение функций и построение графиков функций является одним из основных разделов математики. Умение строить графики часто помогает решать сложные задачи, а иногда является единственным способом их решения. В школьном курсе изучаются построение графиков функций по точкам, при помощи преобразований или с использованием начал анализа. Причем построение графика функций в полярных и декартовых координатах — процесс весьма трудоемкий и занимающий много времени.
В свою очередь, построение графических изображений в Паскале, исследование графиков функций, один из важных и интересных тем программирования. Компьютерная графика в Паскале — область информатики, изучающая методы и свойства обработки изображений с помощью программно-аппаратных средств.
Одним из приложений компьютерной графики является наглядное представление результатов математических расчетов. Графики функций, диаграммы, линии уровней распределения пространственных зависимостей и т. п. делают результаты расчетов обозримее, нагляднее, понятнее. Рассмотрим лишь один простейший вариант математической графики — построение графика функции.
Требуется составить программу построения на экране дисплея графика функции y = F(x).
Решение этой задачи удобно проводить в следующем порядке:
- Определить границы значений аргумента, в пределах которых будет строиться график. Обозначим их следующим образом: Xmin— нижняя граница, Хmax — верхняя граница.
- Для данной области значений аргумента определить предельные значения функции: Ymin и Ymax. Эти значения необязательно должны быть точными. Они могут быть оценочными снизу и сверху соответственно.
- Задать границы графического окна, в пределах которого будет рисоваться график: [Xgmin, Xgmax], [Ygmin, Ygmax]. Поскольку в графических координатах вертикальная ось направлена вниз, то Ygmin>Ygmax. Таким образом, имеем две системы координат: (X, Y), которую назовем системой математических координат (в литературе чаще используют термин «мировые координаты»), и (Xg, Yg) — систему графических координат. Нетрудно получить формулу, связывающую графические и математические координаты:
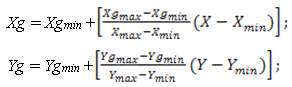 (1)
(1)
Здесь квадратные скобки означают округление до целого значения (функция Round).
Построение графика функции может производиться либо точечным методом, либо кусочно-линейным. При первом способе график строится как последовательность точек, расположенных максимально близко. Производится «попикселевый» перебор значений аргумента в интервале [Xgmin, ![]() ] с выставлением точек с соответствующими координатами Y. При кусочно-линейном методе задается шаг
] с выставлением точек с соответствующими координатами Y. При кусочно-линейном методе задается шаг ![]() Х и рассчитывается последовательность значений (Xi, Yi):
Х и рассчитывается последовательность значений (Xi, Yi):
Xi=Xmax+i![]() Х, Yi=F(Хi), i=0,1,…, n, n=
Х, Yi=F(Хi), i=0,1,…, n, n=![]() .
.
График строится в виде отрезков прямых, проведенных через точки (Xi, Yi), (Xi+1, Yi+1).
Пример 1. Построение графиков функций в декартовых координатах.
Построить графики тригонометрических функций y=sin(x), y=cos(x).
Первым делом, подключаем модуль GraphABC, описываем функции, после чего мы сможем обратиться к ним по именам функций F1 и F2 соответственно. Описываем нужные нам в ходе программирования переменные целого и вещественного типа.
Для того чтобы построить координатные прямые, нам нужно найти координату точки О (точку пересечения осей Х и У). Для этого, ширину экрана и высоту экрана делим пополам, получим координату точки О(x0, y0). График функции лежит в интервале от -![]() , обозначим отрезок через переменные xn=-
, обозначим отрезок через переменные xn=-![]() и xk=+
и xk=+![]() . Подберем более удобный масштаб по формуле (1) mx:=(x0–30)/xk, my:=y0–40. Где x0, y0–начало координат, xk=
. Подберем более удобный масштаб по формуле (1) mx:=(x0–30)/xk, my:=y0–40. Где x0, y0–начало координат, xk=![]() .
.
В результате получится следующая часть программы:
x0:=windowwidth div 2;
y0:=windowheight div 2;
xn:=-2*pi; xk:=2*pi;
mx:=(x0–30)/xk;
my:=y0–40;
Рисуем оси, пересекающиеся в точке О (x0, y0), подписываем их и отмечаем на оси Y интервал [-1,1]. Далее, приступаем к изображению графиков.
Задаем цикл пока: пока ![]() мы наращиваем i (изначально счетчик (i) принимает значение левой границы
мы наращиваем i (изначально счетчик (i) принимает значение левой границы ![]() ), т. е. i:=i+dx и рисуем графики нашей функции, используя формулу (1).
), т. е. i:=i+dx и рисуем графики нашей функции, используя формулу (1).
Получим:
i:=xn;
dx:=0.001;
while i<=xk do
begin
i:=i+dx;
setpixel(x0+round(i*mx),y0-round(F1(i)*my),clBlue);
setpixel(x0+round(i*mx),y0-round(F2(i)*my),clRed);
end;
Напоследок, подписываем полученные функции.
Протокол отладки:
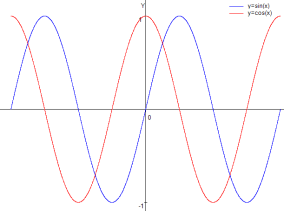
Рис. 1. График функции у = sin (х) и y=cos(x)
Пример 2. Построение графиков функций в полярных координатах.
Построить график «Розы» или кривой Гвидо Гранди — семейство кривых, полярное уравнение которых имеет вид: ![]() , где
, где ![]() — некоторые положительные числа.
— некоторые положительные числа.
Первым делом, подключаем модуль GraphABC. Описываем нужные нам в ходе программирования переменные целого, вещественного и строкового типа и определяем константы ![]() .
.
Для того чтобы построить координатные прямые, нам нужно найти координату точки О (получим, как в предыдущем примере). Следующий шаг — изображение координатной сетки. Для этого вычислим шаг по оси радиуса в пикселях, используя введенное нами значение k. Масштаб для графика найдем по формуле m:=2*(y0–40). Используя цикл for, нарисуем окружности с центром в O(x0, y0) и радиуса=d, где d шаг по оси радиуса в пикселях. Отмечаем шкалу. Шаг по кругу будет равен 30 градусам. Задаем цикл for для того, чтобы нарисовать радиусы пунктиром (радиусов будет 12) и подписываем их. Используя формулу ![]() и знания, о переходе от градусов к радианам, найдем значения x1 и y1.
и знания, о переходе от градусов к радианам, найдем значения x1 и y1.
В результате получится следующая часть программы:
d:=round((y0–40)/(round(k)));
m:=2*(y0–40);
setpencolor(clBlue);
setbrushstyle(bsClear);
for i:=1 to round(k) do
begin
circle(x0,y0,i*d);
str(i/k:0:1,s);
textout(x0-i*d+5,y0+10,s);
end;
f:=30;
for i:=1 to 12 do
begin
Setpenstyle(psDash);
x1:=x0+round((y0–40)*cos(i*f*pi/180));
y1:=y0-round((y0–40)*sin(i*f*pi/180));
end;
Далее, рисуем осевые линии и приступаем к самому графику.
Начальный угол нулевой (x = 0). Задаем цикл пока: пока x≤360 мы вычисляем уравнение в полярных координатах, приводим их к декартовым и к экранным.
x:=0;
while x<=360 do
begin
r:=a*cos(k*x);
xr:=r*cos(x);
yr:=r*sin(x);
x1:=x0+round(m*xr/2);
y1:=y0-round(m*yr/2);
setpixel(x1,y1,clRed);
x:=x+0.01;
end;
Протокол отладки: Рассмотрим при а=1, но при различных k.
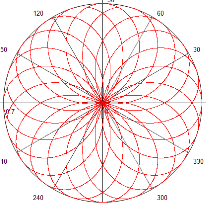

 Рис. 2. График кривой Гвидо Гранди при
Рис. 2. График кривой Гвидо Гранди при ![]()
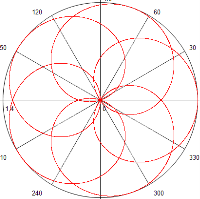

 Рис. 3. График кривой Гвидо Гранди при
Рис. 3. График кривой Гвидо Гранди при ![]()
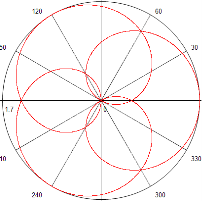

 Рис. 4. График кривой Гвидо Гранди при
Рис. 4. График кривой Гвидо Гранди при ![]()
Данные программы можно использовать на интегрированных уроках информатики и математики, когда учащиеся на уроках информатики практически применяют знания, полученные на уроках математики. Так же на уроках математики при повторении темы: «Полярные координаты», «Графики». Плюс состоит в том, что учителю не потребуется много времени, чтобы изобразить графики на доске. Необходимо только заранее подготовить программы и запустить во время урока, чтобы показать наглядность и решить ту или иную задачу. Конечно же, использовать данные программы можно только после того, как убедились в том, что ученики научились строить графики от руки.

