В настоящее время матричное исчисление широко применяется в различных областях математики, механики, теоретической физики, теоретической электротехники и т. д.
Пусть 
— матрицы 
с комплексными элементами. В данной работе дадим 5 разные доказательство следующего утверждения.
Теорема 1.Матрицы 
и 
имеют одинаковые собственные значение.
Сначала приводим некоторые общеизвестные факты [1–4].
Пусть 
– след матрицы 
, а 
детерминант матрицы 
. Тогда имеют место следующие соотношение:
;(1)
;(2)
и они хорошо известны в курсе линейной алгебры.
Под следом матрицы 
понимают сумму диагональных элементов этой матрицы:
.
Нетрудно видеть, что
,
если 
– характеристические числа матрицы 
.
Доказательство равенство (1) очевидно. Докажем соотношение (2).
Пуст
характеристический многочлен матрицы 
, 
–его корни с учетом кратности. Они являются характеристическими числами матрицы . Известно, что 
является 
–ый элементарный многочлен этих чисел. Следовательно,
;
;
.
Чтобы доказать теоремы 1 надо показать, что
(3)
для всех 
.
Мы знаем, что этот факт верны в случаях 
и 
. Докажем, что оно верна при остальных значениях 
.
Доказательство 1. Достаточно показать равенство
(4)
при всех 
. Подчеркнем, что характеристические числа матрицы 
является 
–ый степень характеристических чисел матрицы 
. Таким образом,
.
Поэтому соотношение (4) эквивалентно следующему
.
С другой стороны из (1) вытекает, что
.
Это и завершает доказательство теоремы 1.
Доказательство 2. Соотношение (3) можно доказать непосредственно. Коэффициент 
является суммой всех принципиальных миноров порядка 
матрицы 
. Прямые вычисления (с помощью формулы Бине–Коши) приводят соотношению (3). Более софистская версия этого аргумента включается анти–симметрической тензорной произведений 
. Оно является матрицей порядка 
, элементы который будут миноры порядка 
матрицы . Тогда
.
Один из важных свойств является следующая:
.
Следовательно,
.
Это и завершает доказательство теоремы 1.
Доказательство 3. Это доказательство вводит аргумент непрерывности, который полезный во многих контекстах. Предположим, что 
обратимая (не сингулярная) матрица. Тогда
.
Поэтому 
и 
являются подобными, и следовательно, имеют одинаковые собственные значение. Таким образом, соотношение (3) верно в случае, когда 
обратимо. Чтобы доказать в общем случае мы нуждаемся два факта: а) Если не сингулярная, мы можем выбрать последовательность не сингулярных матриц 
такое, что 
. б) Функция 
есть многочлен элементов матрицы 
, и следовательно, они непрерывны. Таким образом, если сингулярная, то мы можем выбрать последовательность не сингулярных матриц такое, что и заметим, что
.
Это и завершает доказательство теоремы 1.
Доказательство 4. В этом доказательстве используется блочные матрицы 
. Рассмотрим матрицы 
вида
,
элементы, которых являются матрицы 
, а 
есть нулевая матрица. Характеристические число этой матрицы есть 
характеристические числа матриц 
и 
. Детерминант этой матрицы равно
.
Для любой матрицы 
порядка 
, матрица
порядка является обратимым, и его обратное имеет вид
.
Учитывая этот факт получим, что
.
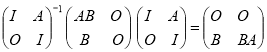Следовательно, матрицы
и
подобны, и поэтому имеют одинаковые характеристические числа. Таким образом, матрицы и имеют одинаковые характеристические числа. Это и завершает доказательство теоремы 1.
Доказательство 5. Пусть 
идемпотентная матрица, т. е. 
. Тогда 
является оператором проектирования (не обязательно ортогональной). В этом случае, некотором базисе (не обязательно ортонормальной) матрица записывается как
.
В этом базисе пусть
.
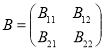Тогда
.
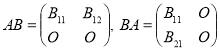Поэтому и имеют одинаковые собственные числа. Пусть теперь произвольная матрица. Тогда существует обратимая матрица 
такое, что
.
Заметим, что 
есть идемпотентная матрица и применяем специальный случай подставляя вместо 
матрицы 
, а вместо 
матрицы 
. Это показывает, что 
и 
имеют одинаковые характеристические числа. С другими словами, и имеют одинаковые характеристические числа. Это и завершает доказательство теоремы 1.
Пусть 
и 
две линейные ограниченные операторы в гильбертовом пространстве 
. Тогда ненулевые элементы спектров операторов 
и 
совпадают.
Пусть и две прямоугольные матрицы. Если обе произведение и имеют смысл, то ненулевые характеристические числа и совпадают.
Литература:
- Ф. Р. Ганхмахер. Теория матриц. — 4-е изд. –М.: Наука, 1988.
- R. Bhatia. Matrix analysis. Springer-Verlag, New York, 1997.
- R. Bhatia. Positive definite matrices. In: Princeton Series in Applied Mathematics. Princeton University Press, 1997
- F. Nielsen, R. Bhatia. Matrix Information Geometry. Springer, XII, 2013, 454.
