Полярное соответствие
— Полярой точки A относительно окружности с центром в O и радиусом R называется прямая a такая, что a OA и OA * OA’ = R 2 , где A’ — основание перпендикуляра, опущенного из O на a.
— Полюсом прямой a относительно окружности с центром в O и радиусом R называется точка A такая, что a OA и OA * OA’ = R 2 , где A’ — основание перпендикуляра, опущенного из O на a.
— Основное свойство полярного соответствия: если поляра точки A проходит через точку B, то поляра точки B так же проходит через точку A (док-во элементарно)
— Если точка A находится вне окружности или на ней, то её поляра относительно совпадает с прямой, проходящей через точки касания и касательных к ней из точки A (док-во элементарно)
— Полярным преобразованием относительно окружности называется преобразование, каждой прямой сопоставляющее её полюс относительно , а каждой точке — её поляру
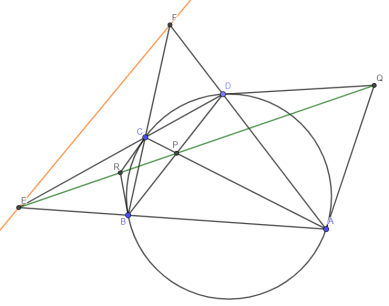
— Теорема Брокара: для вписанного ABCD P — полюс EF
Доказательство:
1) Пусть R — пересечение касательных к в
B и C, а Q — в A и D, тогда, по теореме Паскаля (её док-во см., например, [1]) для AACDDB и для CCABBD имеем
Q — P — E и E — R — P, откуда R — P — Q
2) Т. к. F лежит на полярах R и Q, то RQ есть поляра F P лежит на поляре F F лежит на поляре P. Аналогично и E лежит на поляре P EF есть поляра P P — полюс EF, ч.т.д.
3*) Кроме того, E — полюс PF и F — полюс EF, а также из определения поляр следует, что O — ортоцентр PEF
Теорема о бабочке
— AB — хорда окружности с центром в точке O. На прямой AB выбрана точка P. Перпендикуляр к OP в точке P пересекает касательные к в A и B в X и Y. Докажите PX = PY
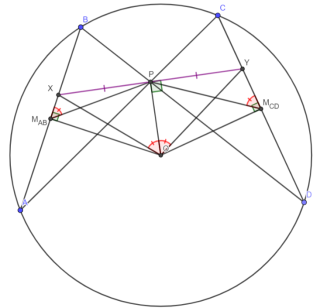
— (Теорема о бабочке) Диагонали вписанного четырёхугольника ABCD пересекаются в точке P, O — центр описанной окружности, докажите, что стороны AB и CD высекают равные отрезки на прямой, перпендикулярной OP и проходящей через P
Доказательство:
1) Пусть X и Y — точки пересечения перпендикуляра к OP в P и сторон AB и CD. Тогда, в силу OM
AB
X = OXP =

2) Поскольку PM AB и PM CD — соответственные элементы подобных треугольников ABP и CDP, то XM AB P = YM CD P XOP = YOP в треугольнике XOY высота OP является биссектрисой, а значит PX = PY, ч.т.д.
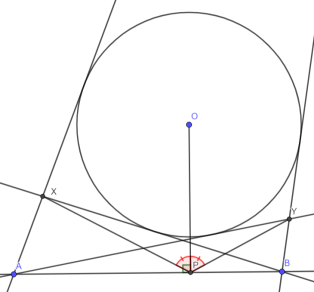
— (Двойственная теорема о бабочке) Из точек A и B проведены касательные к окружности с центром в точке O, пересекающиеся в точках X и Y (на каждой касательной по точке). P — основание перпендикуляра из O на прямую AB. Докажите, что XPO = YPO.
Указание к доказательству: сделайте полярное преобразование относительно , тогда X из теоремы о бабочке перейдет в XP, а Y — в YP. Задача сведется к равенству расстояний от O до XP и YP, что следует из теоремы о бабочке
Теорема Птолемея, её обобщения и еще несколько формул
— Теорема Птолемея: AC * BD = AB * CD + AD * BC (Для доказательства удобно отметить на AC точку X такую, что ABX = DBC и воспользоваться подобием)
— Вторая теорема Птолемея:
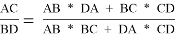
— Теорема Бретшнайдера: для произвольного четырёхугольника ABCD верно
(AC * BD)
2
= (AB * DC)
2
+ (AD * BC)
2–
2 * AB * BC * CD * DA *
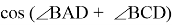
Указание к доказательству: на DA и AB построить PDA и ABQ, подобные ABC и ACD так, чтобы PD оказался || BQ и воспользоваться теоремой косинусов для PAQ
К слову, площадь произвольно четырёхугольника со сторонами a, b, c, d, полупериметром p и противоположными углами и вычисляется по формуле
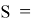
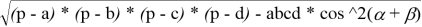
четырёхугольника:
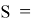

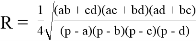
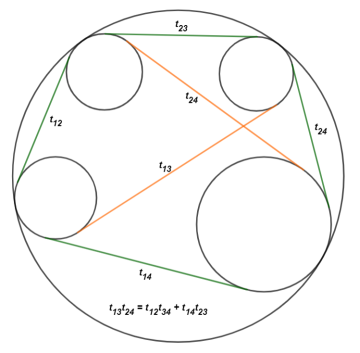
— Теорема Кэзи: для четырёх окружностей, касающихся пятой и имеющих длины касательных (в зависимости от “одноимённости” касания внутренних или внешних) t 12 , t 13 , t 14 , t 23 , t 24 , t 34 верно:
t 13 * t 24 = t 12 * t 34 t 14 * t 23 (Док-во см, например, [5])
Подробнее про теорему Птолемея можно почитать здесь: [4]
Ортодиагональный вписанный четырёхугольник и некоторые свойства замечательных точек
— Теорема Брахмагупты: если AC BD, то M BC P AD
— Свойство 1.1: если AC BD, то (O, CD) =
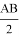
— Свойство 1.2: если AC BD, то проекции P на стороны ABCD и середины этих сторон лежат на одной окружности
Доказательство: постольку P и O изогонально сопряжены (простой счет углов даёт изогональность), то их проекции на стороны лежат на одной окружности, ч.т.д.
— Свойство 1: H ABD H ACD CB — параллелограмм
Доказательство: поскольку каждый из отрезков BH ABD и CH ACD равен 2 * (O, AD) (известное свойство треугольника) и они параллельны, то H ABD H ACD CB — параллелограмм, ч.т.д.
— Свойство 2: AI ABD I ACD D — вписанный
Доказательство: по лемме о трезубце для ABD и для ACD LA = LI ABD = LD и LA = LI ACD = LD, где L — середина дуги AD AI ABD I ACD D — вписанный, ч.т.д.
— Японская теорема: I ABD I ACD I BCD I ABC — прямоугольник
Доказательство: используя свойство 2 получаем: I
ABC
I
ABD
I
ACD
= 2 — AI
ABD
I
ACD
—
AI
ABD
I
ABC
= ABI
ABC
+ ADI
ACD
=

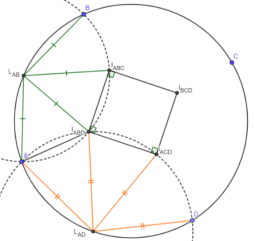
— Свойство 3: P, O и точка пересечения перпендикуляров к BC и AD, восстановленных в C и D соответственно, лежат на одной прямой.
Доказательство:
1) Пусть Q и T — точки пересечения перпендикуляров к BC и AD, восстановленных в C и D и в B и A соответственно, а K и L — проекции P на BC и AD, тогда, очевидно, Q, O и T коллинеарны и достаточно проверить равенство
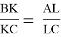
(От противного легко проверить, что если на некоторых прямых отметить точки A, B, C и A’, B’, C’ так, что
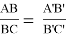
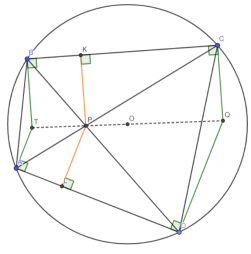
“Школьные” методы доказательства некоторых теорем
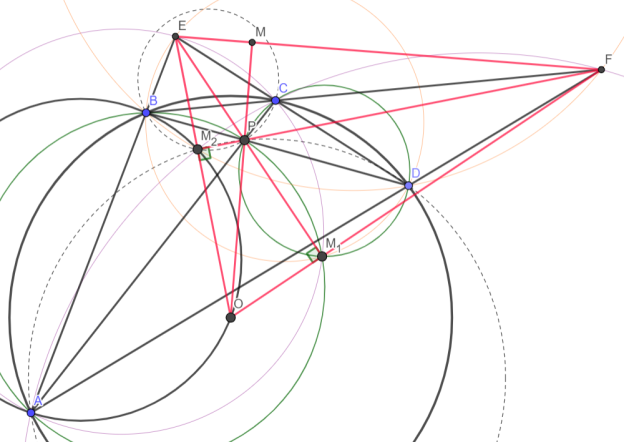
— Пусть (ABP) ∩ (CDP) = M 1 , (BCP) ∩ (ADP) = M 2 , тогда
1) M 1 и M 2 будут точками Микеля ломаных ACDB и ACBD. Отсюда моментально получаем вписанность ECM 1 A, EDM 1 B, FCM 2 A, FDM 2 B
2) E — P — M 1 и F — P — M 2 как радикальные оси зелёных и пунктирных окружностей (см. чертёж)
3) AOB = ADP + BCP = AM 2 B (из пунктирных окружностей) AOM 2 B — вписанный, аналогично DOM 2 C, BOM 1 C и AOM 1 D тоже вписанные, тогда, опять же как радикальные оси описанных окружностей этих четырехугольников, E — M 2 — O, F — M 1 — O, кроме того,
EM 2 * EO = EB * EA = EP * EM 1 , откуда OPM 1 M 2 — вписанный
4) OM
2
* OE = OE
2
— EM
2
* OE = OE
2
— (OE
2
— R
2
) (квадрат касательной) = R
2
, аналогично OM
1
* OF = R
2
EM
2
M
1
F — вписанный, но, в силу вписанности и OPM
1
M
2
, OM
2
P = OM
1
P =

5) Кроме того, FM * FE = FP * FM 2 = FC * FB CEMB — вписанный, аналогично DFMC вписанный
M — точка Микеля ABCD O — P — M
6) Легко проверить, что AMO = AMC, тогда, т. к. OA = OC, AOCM будет вписанным по признаку. Аналогично и BODM
Задачи
-
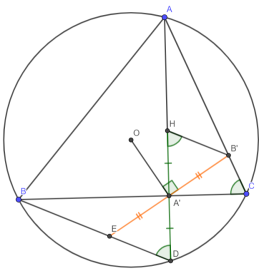
(Из материалов IMO, 1996) O и H — центр описанной окружности и точка пересечения высот треугольника ABC соответственно. A’ — основание высоты из A на BC. Точка B’ на AC такова, что B’A’O =

Решение:
1) Пусть AA’ ∩ описанную окружность в точке D, а A’B’ BD — в E
2) Широко известно, что HA’ = A’D, кроме того, по теореме о бабочке B’A’ = A’E; HA’B’ и EA’D — вертикальные A’ED = HA’B’
3) BCA = A’DE = A’HB’, ч.т.д.
- (Теорема Фейербаха). Окружность девяти точек треугольника касается его вписанной и вневписанных окружностей.
Доказательство:
1) Пусть A’, B’ и C’ — середины BC, AC и AB соответственно, а A
1
, B
1
и C
1
— точки касания вписанной окружности со сторонами; BC = a, AC = b, AB = c, p =
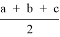
2) Если рассматривать A’, B’ и C’ как окружности нулевого радиуса, то нам достаточно проверить условие обратной теоремы Кэзи: A’C’ * B’B
1
= A’A
1
* B’C’ + C’C
1
* A’B’, т. е.
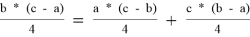
3) Аналогично и с вневписанными окружностями
- (Л. А. Емельянов) Пусть ABC — произвольный треугольник, а M — точка внутри треугольника. Проведём через точку M три чевианы, основания которых — A 1 , B 1 , C 1 . Построим вне треугольника три окружности, касающиеся сторон треугольника в основаниях чевиан и описанной окружности, и четвёртую, касающуюся этих трёх внешним образом. Тогда эта окружность касается вписанной окружности треугольника внутренним образом.
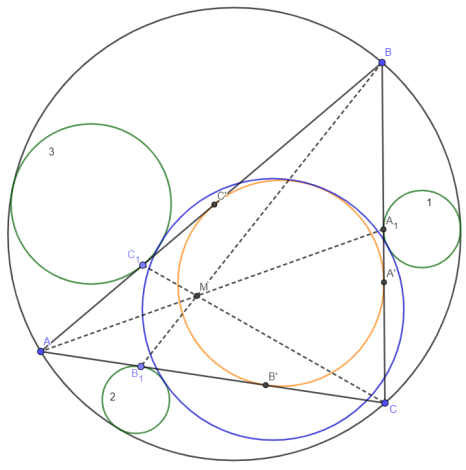
1) Обозначим для удобства AB = c, AC = b, BC = a, p =
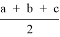
2) Применим теорему Кэзи для A, B, 1, C: t
1
A
t
BC
= t
AB
t
1
C
+ t
AC
t
1
B
, откуда t
1
A
=
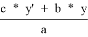
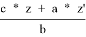
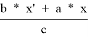
3) Применим теорему Кэзи для B, C, 2, 3: t
3
C
t
2
B
= t
CB
t
23
+ t
2
C
t
3
B
, откуда, подставляя результаты п.2: t
23
=
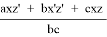
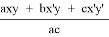
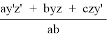
4) t 1 = (p — c) — y’, t 2 = z’ — (p — a), t 1 = x’ — (p — b). Подставим полученные выражения в условие обратной теоремы Кэзи для 1, 2, 3 и :
t
12
t
3
— t
13
t
2
— t
23
t
1
=
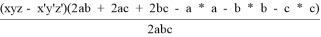
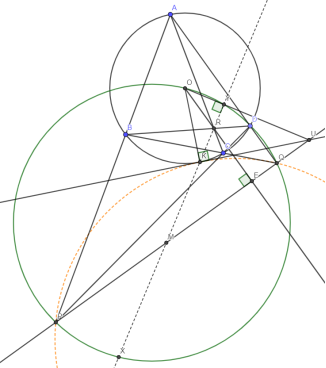
- (Romanian Masters, 2013, задача 3, автор — М. А. Кунгожин) Четырёхугольник ABCD вписан в окружность . Прямые AB и CD пересекаются в точке P, AD и BC — в Q, диагонали AC и BD — в R. Пусть M — середина PQ. Точка K — общая точка прямой MR и . Докажите, что описанная окружность KPQ касается .
Решение:
1) Пусть O — центр , Y — проекция O на MR, OY ∩ PQ = U.
2) По теореме Брокара PQ — поляра R по основному св-ву полярного соответствия R лежит на поляре U. Но MR OU MR — поляра U UK — касательная к UK 2 = UY * UO (из пр/у треугольника OKU)
3) По теореме Брокара R — ортоцентр OPQ X, симметричная R относительно M, (OPQ) (PXQ = PKQ =

Задачи для самостоятельного решения
- Дан вписанный шестиугольник A 1 A 2 A 3 A 4 A 5 A 6 . Докажите, что A 1 A 4 *A 2 A 4 *A 3 A 6 = A 1 A 2 *A 3 A 6 *A 4 A 5 + A 2 A 3 *A 1 A 4 *A 5 A 6 + A 3 A 4 *A 2 A 5 *A 6 A 1 .
- Высоты BB’ и CC’ треугольника ABC пересекаются в точка H. Прямая B’C’ пересекает прямую BC в точке E. M — середина BC. Докажите, что MH AE.
- H — точка пересечения высот ABC, M — середина BC. Перпендикуляр к MH в H пересекает прямые AB и AB в X и Y. Докажите, что HX = HY.
- Вневписанная окружность треугольника ABC, касающаяся стороны BC, касается AB, CB и AC в C 1 , A 1 и B 1 — соответственно. I — центр вписанной окружности ABC. IX и IY — касательные из I к вневписанной окружности, касающейся BC. Докажите, что середины отрезков C 1 A 1 и B 1 A 1 и точки X и Y лежат на одной прямой.
- (Польская национальная олимпиада, финал, задача 5. Автор — Dominik Burek) Точка M — середина стороны BC треугольника ABC. Точка P на стороне AB такова, что AP > BP. Точка Q на стороне AC такова, что ∠BPM = ∠CQM. Серединные перпендикуляры к BC и PQ пересекаются в точке S. Докажите, что ∠BAC + ∠QSP = ∠QMP.
- (ВСОШ, заключительный этап, 2009/2010, 11.3) Четырехугольник ABCD вписан в окружность ω, а его диагонали пересекаются в точке K. Точки M 1 , M 2 , M 3 , M 4 — середины дуг AB, BC, CD, DA (не содержащих других вершин четырехугольника) соответственно. Точки I 1 , I 2 , I 3 , I 4 — центры окружностей, вписанных в треугольники ABK, BCK, CDK, DAK соответственно. Докажите, что прямые M 1 I 1 , M 2 I 2 , M 3 I 3 , и M 4 I 4 пересекаются в одной точке.
- Вписанная окружность треугольника ABC с центром I касается стороны AC в точке Q; точка E — середина стороны AC, а K — точка пересечения высот треугольника BIC. Докажите, что KQ IE.
- ABCD — описанный четырёхугольник. AB ∩ CD = E, AD ∩ BC = F, AC ∩ BD = P. X — основание перпендикуляра из P на EF. Докажите, что AXP = PXC.
-
(По мотивам Romanian Masters, 2013, задачи 3) Четырёхугольник ABCD вписан в окружность . Прямые AB и CD пересекаются в точке P, AD и BC — в Q, диагонали AC и BD — в R. Пусть M — середина PQ. Прямая MR пересекает в точках K и L. Докажите, что PKQ + PLQ =
- (XVIII олимпиада имени И. Ф. Шарыгина, финал, 10 класс, задача 4, авторы — А. Матвеев, И. Фролов) Выпуклый четырехугольник ABCD таков, что ∠B = ∠D. Докажите, что середина диагонали BD лежит на общей внутренней касательной к окружностям, вписанным в треугольники ABC и ACD.

