При выборе напорного устройства системы охлаждения крупных электрических машин с внутренней полостью, заполненной жидким диэлектриком, [1] приходится учитывать то обстоятельство, что в так называемом «воздушном зазоре» машины (кольцевом канале) и в осевых каналах ротора (каналы круглого сечения, вращающиеся вокруг параллельной им внешней оси) течение жидкости происходит в дополнительном поле центробежных сил.
Для теоретического изучения влияния центробежных сил на движение жидкости в указанных выше каналах необходимо, чтобы они вошли в соответствующие уравнения, то есть, чтобы эти силы были внешними. Это, как известно, может быть достигнуто в том случае, если анализировать относительное движение.
Общее уравнение относительного напорного установившегося движения жидкости, составленное из основных размерных переменных параметров, характеризующих упомянутое движение, можно представить в виде:
для кольцевого канала
F1 (r1, d, D, qZ, qf, Dр, ац, g, r, n) = 0; (1)
для осевого канала
(2)
Введенные в уравнение (1) и (2) параметры относятся к трем категориям:
1) характерные линейные размеры, определяющие границы области (радиус 
внутренней цилиндрической поверхности и высота 
кольцевого канала, внутренний диаметр 
осевого канала,
шероховатость стенок каналов D);
2) кинематические и динамические характеристики движения (осевая qz и вращательная 
компоненты средней относительной скорости в кольцевом канале, средняя относительная скорость 
в осевом канале, перепад давления Dр в каналах, среднее центробежное ускорение 
, действующее на частицы жидкости в кольцевом канале, равное 
, где rс — средний радиус вращения, равный rс = 0,5d; среднее центробежное ускорение 
действующее на частицы жидкости в осевом канале, равное 
где 
-линейная скорость канала на радиусе 
вращения его оси; ускорение свободного падения g);
3) физические свойства жидкости (плотность r, кинематический коэффициент вязкости n).
Зависимостям (1) и (2) можно придать более определенный вид, сгруппировав все переменные размерные величины в безразмерные комплексы с использованием 
- теоремы. В данном случае упомянутыми безразмерными комплексами являются:
для кольцевого канала
1) число Эйлера 5) число Фруда
; 
2) «осевое» число Рейнольдса 6) относительная шероховатость
; 
3) «окружное» число Рейнольдса 7) симплекс
; 
.
4) число Тейлора
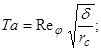
для осевого канала
1) число Эйлера 4) параметр ориентации
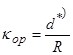
2) число Рейнольдса 5) число Фруда
3) параметр вращения 6) относительная шероховатость
.
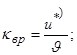
*) Терминология, принятая, согласно [2].
Средняя линейная скорость вращения жидкости в кольцевом канале может быть представлена в виде:
(3)
где 
- средняя угловая скорость вращения жидкости.
В узких кольцевых каналах 
Учитывая сказанное и опуская индекс «с» при угловой скорости 
в формуле (2), выражение для окружного числа Рейнольдса 
и для числа Тейлора Та принимают вид:
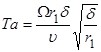, (4)
где — угловая скорость на радиусе 
Если геометрические размеры канала известны и заданы скорости 
, 
,то числа 
Та, 
являются критериями, входящими в нижеследующие критериальные уравнения:
для кольцевого канала
(5)
или
(6)
для осевого канала
. (7)
Естественно, что отыскание функциональной зависимости числа Эйлера от столь большого числа одновременно действующих переменных величин, представляет собой трудную задачу. Очевидно, что эти переменные в зависимости от условий движения жидкости могут в различной степени влиять на 
Задача может быть значительно облегчена в том случае, если представится возможность изучать движение жидкости в таких условиях, которые позволят исключить из рассмотрения некоторые переменные в зависимостях (5 ¸ 7). Иными словами, если представится возможность ограничить число переменных теми из них, которые главным образом характеризуют поток в данных условиях и влияют на потери напора.
В рассматриваемых здесь крупных электрических машинах с жидкостным охлаждением даже при сравнительно небольших частотах вращения ротора (300–500 
) величина центробежного ускорения 
составляет порядка 100g, благодаря чему влиянием ускорения силы тяжести g на поток можно пренебречь и число Фруда из уравнений (5 ¸ 7) исключить. Кроме того, течение жидкости в рассматриваемых каналах будет происходить при значениях чисел Рейнольдса, соответствующих ламинарному и начальной стадии турбулентного режимов движения, при которых, как известно, влиянием относительной шероховатости на потери напора можно пренебречь.
С учетом сказанного, зависимости (5 ¸ 7) примут вид:
для кольцевого канала
(8)
или
(9)
для осевого канала
(10)
Свяжем перепад давления 
в каналах со средней скоростью и течения жидкости в них следующими зависимостями:
для кольцевого канала
(11)
для осевого канала
(12)
где l — длина канала; 
- так называемый гидравлический диаметр; - диаметр канала; 
- некоторый коэффициент пропорциональности.
Подставляя (11) и (12) в полученные выше выражения для чисел Эйлера найдем, что в подобных каналах в роли числа Эйлера будет выступать коэффициент 
Имея это в виду, уравнения (8 ¸10) перепишем в виде:
для кольцевого канала
(13)
или
(14)
для осевого канала
(15)
Таковы критериальные уравнения относительного плавно изменяющегося напорного движения жидкости в кольцевом и осевом каналах.
Из рассмотрения этих уравнений видно, что , также как и коэффициент гидравлического трения 
(учитывающий потери напора по длине в канале с неподвижными стенками), зависит от скорости осевого движения жидкости в канале и геометрических характеристик канала и кроме того, дополнительно, от скорости вращательного движения.
Вместе с тем, выполненный нами анализ уравнений (13) и (14) показал, что существует область автомодельности относительно скорости вращательного движения (относительно числа Тейлора), причем в этом случае величину можно вычислять по известной формуле:
(16)
Выводы
В системах охлаждения крупных погружных электродвигателей, заполненных жидким диэлектриком в целях интенсификации процесса теплообмена, необходимо обеспечить непрерывную циркуляцию жидкого диэлектрика внутри машины напорным устройством.
При определении напорно-расходной характеристики напорного устройства необходимо учитывать, что в кольцевом канале («воздушном зазоре») машины и в осевых каналах ротора течение жидкости происходит в дополнительном поле центробежных сил.
Определены этапы теоретического изучения влияния центробежных сил на движение жидкости в указанных выше каналах.
Получены и проанализированы критериальные уравнения относительного плавно изменяющегося напорного движения жидкости в кольцевом и осевом каналах.
Показано, что область ламинарного с отсутствием вихрей Тейлора течения жидкости в кольцевом канале, является областью автомодельности коэффициента относительно скорости вращательного движения.
Литература:
1. Денисов В. А., Полубояринов Ю. Г. Применение встроенных насосов в системах охлаждения жидкостно-заполненных герметичных электродвигателей. Межвузовский сборник: СЗПИ, № 37, 2007.
2. Квитковский Ю. В. Гидромеханическое подобие и кинематическая структура аксиальных потоков жидкости // Тр.МИИТ, 1976, вып. 525, с.4–11.
