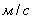Кинематическое исследование кулисного механизма для привода рабочего органа поршневого насоса для вязких и неоднородных жидкостей

В рассматриваемом кулисном механизме кривошипно-шатунного рабочего органа поршневого насоса вес звенья параметров данного механизма можно условно разделить на две части — кулисного механизма и кривошипно-шатунного рабочего органа поршневого насоса. Заключительную часть выполнения технологической части работы составляет кривошипно-шатунный поршень, поэтому, данное звено мы называли кулисный механизм поршневого насоса.

Основная деталь узла механизма (рисунок 1, а) — поршень 6 перемещающаяся в цилиндре 7. Наружная поверхность поршня 6 плотно прилегается к обработанной поверхности цилиндра 7. Поршень движется возвратно-поступательно и совершает движение под воздействием кривошипно-шатунного механизма (1, 2, 3) воздействующего на шток 5. При движении ползуна 2 вправо поршень 6 совершает рабочий ход 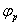, а при движении ползуна 2 влево происходит холостой ход .

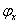Для преобразования вращательного движения кривошипа 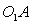 в возвратно-поступательное движение ползуна 2 применяется кулисный механизм 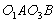. Кривошип 9 вращается со средней угловой скоростью 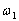, а кулиса  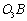качается относительно точки 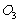. Кулисный механизм позволяет получить большую скорость  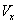холостого хода, чем скорость  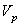рабочего хода поршня, т. е. 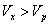. Величину хода  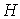поршня можно изменять в зависимости от изменения длины радиуса  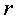кривошипа : .

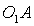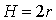Кривошипно-шатунный механизм применяется для преобразования непрерывного вращения ведущего звена-кривошипа 1 в возвратно-поступательное движение ведомого звена — поршня в бетононасоса и, наоборот, для преобразования поступательного движения поршня 6 в непрерывное движения кривошипа 1.

Скорость точки 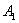 звена кривошипа кулисного механизма определяем аналитически по формуле

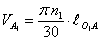                                                                                                              (1)

где 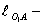длина радиуса кривошипа 1 кулисного механизма, ;

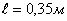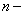частота вращения кривошипа, .

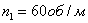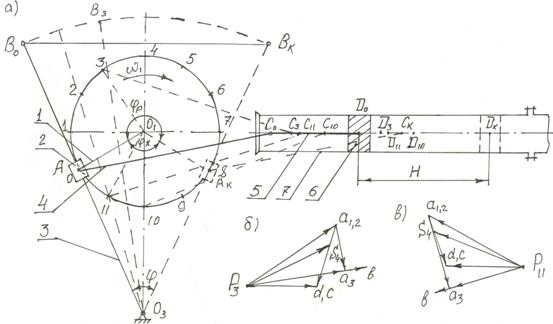
Рис. 1. Кинематическая схема кулисного механизма (а) и плана скоростей (б, в) звеньев механизма

Подставляя численные значения, получим

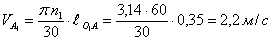
Вектор скорости точки 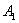 направлена перпендикулярно кривошипа 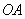. Скорости точек других звеньев кулисного механизма определяем путем построения планов скоростей с использованием векторных уравнений связывающих скоростей для структурной группы из звеньев ползуна 12 и кулисы 13.

Векторная скорость точки 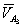 кулисы составляется два векторных уравнения, в которых искомая скорость  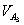связывается с известными скоростями точек  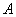ползуна и  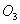кулисы, имеют вид:

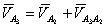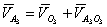;                                                                                (2)

где 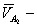скорость точки  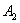звена ползуна, которая совмещена с точкой  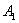звена кривошипа и считается принадлежащей ползуну 2. По модулю она равна величине  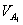и направлена также перпендикулярно к линии  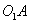в сторону вращения кривошипа;

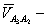скорость точки  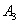звена кулисы 3 относительно точки  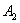ползуна, направлена параллельно кулисе  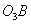и неизвестна по модулю;

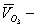скорость данного звена  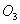равна нулю, так как точка  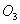относится к неподвижной стойке кулисы;

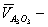скорость точки  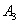звена считается принадлежащей кулисе 3, поэтому скорость точки  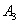при вращении её вокруг стойки  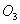неизвестна по модулю и направлена перпендикулярно к линии  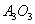кулисы .

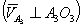Для определения скорости 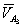 необходимо графическое решение векторных уравнений (2) из произвольной точки  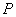(полюс плана) в направлении вектора  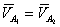откладываем отрезок  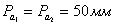(рисунок 1, в). Тогда масштаб скоростей будет

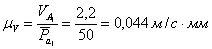
Из точки 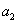 отрезка  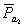проводим линию направления вектора 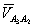, а из полюса  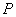(т. к. 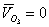) — по линию направления вектора 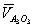. На пересечении этих линий находим точку  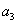и соединив ее с полюсом получим отрезок 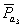, изображающий скорость .

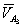Кулисный механизм служит приводом рабочего органа поршневого насоса, в котором кривошип через ползуна 2 и шатуна 4 соединен со штоком 7 поршня 6. Векторные уравнения скоростей группы звеньев шатуна 4 и штока 7 (поршня 6) записываются в виде

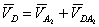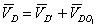;                                                                                    (3)

где 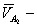скорость точки  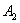звена ползуна, которая совмещена с точкой  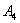звена шатуна, направлена перпендикулярно кривошипу  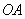по направлению его вращения;

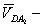скорость точки  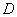звена штока относительно точки  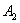ползуна, направлена перпендикулярно звену шатуна ;

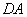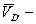скорость равна нулю, т. к. точка  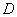звена лежит на неподвижной направляющей ;

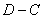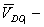скорость перемещения точки  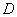звена штока по направляющей, направлена параллельно ее оси и неизвестна по модулю.

Для графического решения уравнения (3) из конца вектора 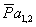 проводим линию направления вектора 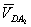, а из полюса  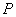(т. к. 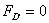) — линию направления вектора 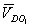. На пересечении двух линий отмечаем точку  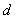и соединив ее с полюсом получим отрезок  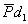изображающий вектор .

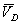Истинное значение скорости каждой точки определяем по формулам:

; ;

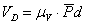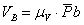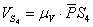
Планы скоростей строим для всех 12 ти положений кулисного механизма. На рисунке 1, в приводится план скоростей механизма для 3 позиции. Полученные числовые значения скоростей поршня 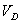, кривошипа  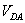и центра масс шатуна  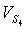сводим в таблицу 1.

В кулисных и поршневых механизмах различают рабочий и холостой ход так называемые фазовые углы — 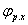 и 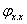. Рабочий фазовых угол  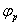равно позициям от 0 до 7, а холостой фазовый угол  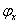— от 7 до 0. Тогда средняя скорость  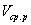рабочего фазового угла будет:

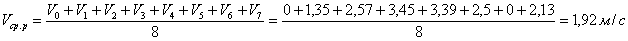Средняя скорость холостого фазового угла будет:

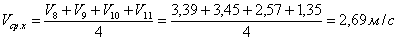
По отношению средних скоростей холостого и рабочего хода поршня находим коэффициента 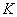 изменение скорости хода поршня

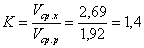
Следовательно, при равномерном вращении кривошипа кулисного механизма скоростные параметры рабочего хода от холостого хода отличается в 1,4 раза, что значительно увеличивается надежность и срок службы механизма.