Производство бетонных смесей на заводах с большой производительностью позволяет достигнуть выработки до 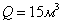 на одного рабочего в смену, что снижает стоимость приготовления бетонных смесей в 5–8 раз по сравнению с приготовлением их на мелких установках. Для доставки бетонных смесей к месту укладки применяются бетононасосы. Главным параметром этих насосов является производительность.
на одного рабочего в смену, что снижает стоимость приготовления бетонных смесей в 5–8 раз по сравнению с приготовлением их на мелких установках. Для доставки бетонных смесей к месту укладки применяются бетононасосы. Главным параметром этих насосов является производительность.
Нами предлагается кинематическая схема (рисунок 1) кулисного механизма с планетарной передачей для привода рабочего органа поршневого насоса при транспортирования бетонных смесей. С помощью предлагаемого бетононасоса возможно перемещение бетонов на расстояние до 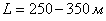 по горизонтали, а также подъем на высоту до
по горизонтали, а также подъем на высоту до 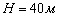 . Данная производительность является в два раза больше, чем серийные кривошипно-шатунные бетононасосы. Бетонная смесь (рисунок 1, а) из приемного бункера 1 подается лопастными устройствами 1 и 3, в котором она непрерывно перемещается, к всасывающему клапану 4 цилиндра 5 насоса. После заполнения цилиндра 5 всасывающий клапан 4 закрывается и открывается последующий клапан 6 нагнетания. Основная деталь бетононасоса — поршень 6, перемещающаяся в цилиндре 5. Поршень движется возвратно-поступательно и совершает движение под воздействием кривошипно-шатунного механизма (7, 8, 9) воздействующего на шток 7. При движении ползуна 12 вправо поршень 6 совершает рабочий ход, а при движении ползуна 12 влево происходит холостой ход.
. Данная производительность является в два раза больше, чем серийные кривошипно-шатунные бетононасосы. Бетонная смесь (рисунок 1, а) из приемного бункера 1 подается лопастными устройствами 1 и 3, в котором она непрерывно перемещается, к всасывающему клапану 4 цилиндра 5 насоса. После заполнения цилиндра 5 всасывающий клапан 4 закрывается и открывается последующий клапан 6 нагнетания. Основная деталь бетононасоса — поршень 6, перемещающаяся в цилиндре 5. Поршень движется возвратно-поступательно и совершает движение под воздействием кривошипно-шатунного механизма (7, 8, 9) воздействующего на шток 7. При движении ползуна 12 вправо поршень 6 совершает рабочий ход, а при движении ползуна 12 влево происходит холостой ход.
Для преобразования вращательного движения кривошипа 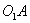 в возвратно-поступательное движение ползуна 12 применяется кулисный механизм
в возвратно-поступательное движение ползуна 12 применяется кулисный механизм 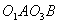 . Кривошип 9 вращается со средней угловой скоростью
. Кривошип 9 вращается со средней угловой скоростью 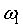 , а кулиса
, а кулиса 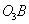 качается относительно точки
качается относительно точки 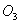 . Кулисный механизм позволяет получить большую скорость обратного хода, т. е. холостого хода. Для получения нужной основной скорости поршня служит коробка передач. Величину хода
. Кулисный механизм позволяет получить большую скорость обратного хода, т. е. холостого хода. Для получения нужной основной скорости поршня служит коробка передач. Величину хода 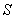 поршня можно изменять в зависимости от изменения длины радиуса
поршня можно изменять в зависимости от изменения длины радиуса 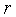 кривошипа
кривошипа 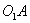
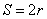 (1)
(1)
При заданной величине хода поршня 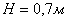 определяем длину радиуса кривошипа
определяем длину радиуса кривошипа 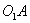 , т. е.
, т. е. 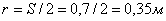 . Кривошипно-шатунный механизм применяется для преобразования непрерывного вращения ведущего звена-кривошипа 9 в возвратно-поступательное движение ведомого звена — поршня в бетононасоса и, наоборот, для преобразования поступательного движения поршня 6 в непрерывное движения кривошипа 9. Перемещение ползуна 12, в кулисном механизме из одного крайнего положения
. Кривошипно-шатунный механизм применяется для преобразования непрерывного вращения ведущего звена-кривошипа 9 в возвратно-поступательное движение ведомого звена — поршня в бетононасоса и, наоборот, для преобразования поступательного движения поршня 6 в непрерывное движения кривошипа 9. Перемещение ползуна 12, в кулисном механизме из одного крайнего положения 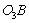 в другое
в другое 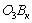 происходит при повороте кривошипа на угол
происходит при повороте кривошипа на угол 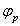 , а обратный ход коромысла — во время поворота кривошипа 9 на угол
, а обратный ход коромысла — во время поворота кривошипа 9 на угол 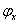 . Углы
. Углы 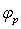 и
и 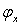 будем называть фазовыми углами соответственно прямого — рабочего и обратного — холостого ходов:
будем называть фазовыми углами соответственно прямого — рабочего и обратного — холостого ходов:
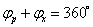 (2)
(2)
Разность между каждым из этих углов и 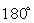 обозначается углом
обозначается углом 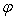 — размаха кулисы, которая определяется:
— размаха кулисы, которая определяется:
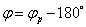 (3)
(3)
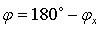 (4)
(4)
Отношение этих углов называется коэффициентом 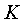 изменения скорости хода поршня:
изменения скорости хода поршня:
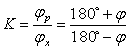 (5)
(5)
отсюда находим угол 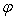 размаха кулисы
размаха кулисы
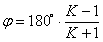 (6)
(6)
В кривошипно-ползунных механизмах при разных звеньев фазовый угол 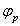 может иметь величину от
может иметь величину от 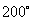 практически примерно до
практически примерно до 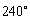 , т. е. коэффициент
, т. е. коэффициент 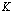 изменения скорости хода поршня бетононасоса может изменяться в следующем интервале
изменения скорости хода поршня бетононасоса может изменяться в следующем интервале 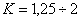 .
.
Коэффициент увеличения средней скорости кулисы будет
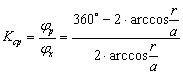 (7)
(7)
Подставляя численные значения радиуса кривошипа, 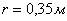 и
и 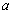 - межосевого расстояния кулисного механизма,
- межосевого расстояния кулисного механизма, 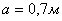 в уравнение (6) получим:
в уравнение (6) получим:
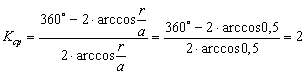
и, следовательно, разница в интервалах прямого 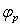 и обратного
и обратного 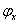 ходов возрастает по мере приближения межосевого расстояния кулисы к радиусу
ходов возрастает по мере приближения межосевого расстояния кулисы к радиусу 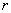 .
.
По коэффициенту увеличения средней скорости 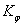 определяем угол
определяем угол 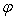 размаха качающейся кулисы
размаха качающейся кулисы 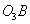 :
: 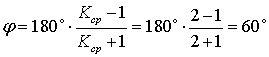
Находим длину радиуса качающейся кулисы 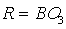 данного механизма:
данного механизма:
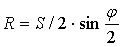 (8)
(8)
а также параметр высоты катета 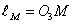 кулисного механизма:
кулисного механизма:
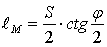
 (9)
(9)
где 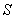 - ход вершины
- ход вершины 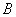 кулисы
кулисы 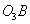 кулисного механизма.
кулисного механизма.
В обоих уравнениях (8) и (9) имеем по две неизвестных: радиуса 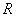 качающейся кулисы (катета
качающейся кулисы (катета 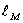 ) и хода
) и хода 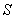 кулисного механизма, поэтому длину радиуса
кулисного механизма, поэтому длину радиуса 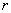 кривошипа и межосевое расстояния
кривошипа и межосевое расстояния 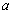 кулисного механизма подбираем таким образом, чтобы соблюдалось условие:
кулисного механизма подбираем таким образом, чтобы соблюдалось условие:
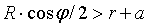 (10)
(10)
Подставляя численные значения радиуса кривошипа 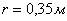 и межосевое расстояние
и межосевое расстояние 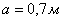 кулисного механизма, получим:
кулисного механизма, получим: 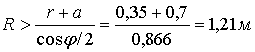
Принимаем радиус 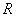 качающегося кулисы,
качающегося кулисы, 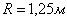 , тогда подставляем данное значение в уравнение (7) получим длину хода
, тогда подставляем данное значение в уравнение (7) получим длину хода 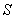 качающейся кулисы:
качающейся кулисы: 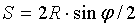
Подставляя численные значения 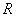 и
и 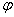 , получим:
, получим:
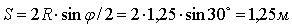
Полученное данное численные значения хода 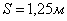 кулисы подставляем в уравнение (9) получим высоту катета
кулисы подставляем в уравнение (9) получим высоту катета 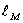 кулисного механизма:
кулисного механизма:
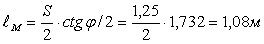
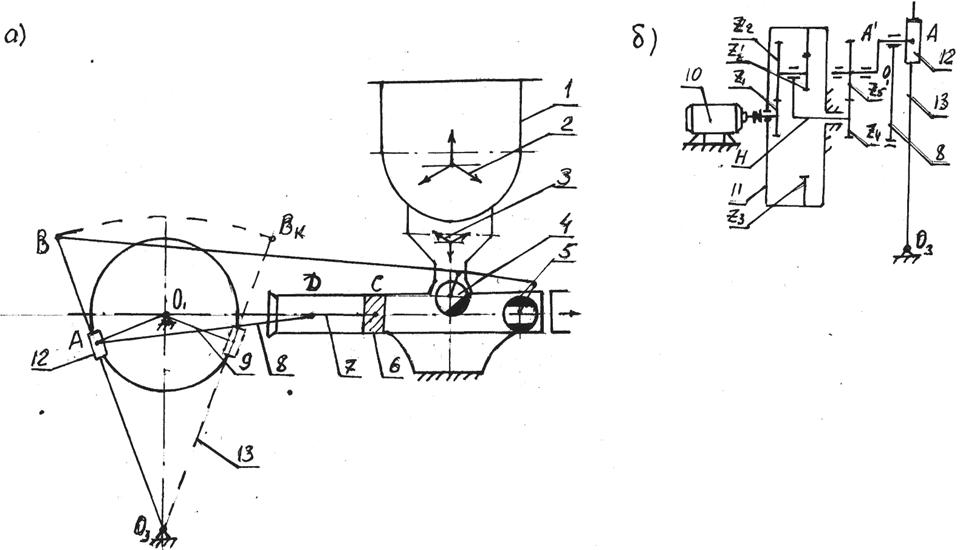
Рис. 1. Кинематическая схема кулисного механизма (а) и привода (б) рабочего органа поршневого насоса.
При этом если подставим полученные значения 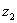 в уравнения (1), то получим:
в уравнения (1), то получим:
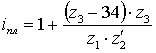 ,
,
подставляя численные значения 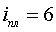 ;
; 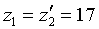 получим:
получим:
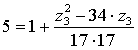
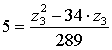
Решая данное уравнение будем иметь:
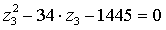
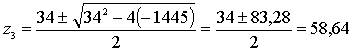
Принимаем 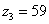 , тогда подставляя
, тогда подставляя 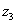 в уравнение (2) получим численное значения
в уравнение (2) получим численное значения 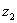 :
:
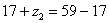
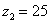
Второе конструктивное условие ограничивает число 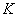 сателлитов
сателлитов 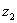 и
и 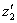 планетарной передачи таким образом, чтобы зубья колес смежных сателлитов, устанавливаемых вокруг центрального
планетарной передачи таким образом, чтобы зубья колес смежных сателлитов, устанавливаемых вокруг центрального 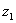 и коронного
и коронного 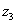 зубчатого колеса не пересекались между собой. Условие соседства смежных сателлитов для заданной схемы планетарного редуктора пишется в виде:
зубчатого колеса не пересекались между собой. Условие соседства смежных сателлитов для заданной схемы планетарного редуктора пишется в виде:
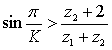 (11)
(11)
Отсюда определяем максимальное количество 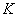 расположение сателлитов в планетарном передаче:
расположение сателлитов в планетарном передаче: 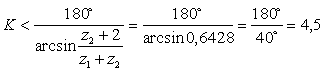
По расчету вполне можно установить в данном планетарном редукторе количество сателлитов 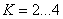 . Принимаем
. Принимаем 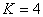 .
.
Также второе конструктивное условие выполнено. Третьим конструктивным условием является обеспечение возможности сборки планетарного редуктора, когда
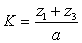 (12)
(12)
где: 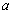 — произвольное целое число.
— произвольное целое число.
Из уравнения (12) находим произвольное целое число 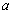 :
:
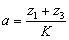
Подставляя численное значение 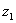 ,
, 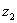 и
и 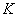 равный
равный 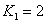 ,
, 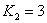 и
и 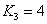 .
.

