Материал оболочки (бетон) предполагается при сжатии нелинейно-упругим, при растяжении работающей с трещинами. Закон деформирования бетона описывается при кратковременном загружении нелинейными алгебраическими уравнениями, а при длительном действии нагрузки – уравнениями нелинейной наследственной теории ползучести.
Несущая способность оболочки оценивается с учетом неупругого деформирования конструкции, на основе экспериментально установленных закономерностей, полученных при испытании конических куполов и его элементов.
Для оценки напряженно-деформированного состояния конических оболочек считается целесообразным применение разрешающего уравнения с учетом влияния краевого эффекта возникающего вблизи опорного кольца конических оболочек.
, 
.(1)
Если учесть, что
; 
(2)
то при этом длина образующей sотcчитывается от вершины конуса.
С учетом (1) усилия в срединной поверхности купола можно определить по выражениям
;
(3)
Усилия N1 и Q выражаются через распорную силу N2и известные осевые усилия V (s) в сечении оболочки определяется по формулам
,(4)
,(5)
где N2 = 
.
Для линейно деформированной оболочки радиальное 
, осевое перемещение 
и угол поворота нормали 
представим в виде
, 
,(6)
при аналогичных предположениях 
представим
.(7)
Деформации срединной поверхности оболочек 
и параметры изменения её кривизны 
могут быть выражены через две деформации. Для линейно деформированной оболочки радиальное , осевое перемещение и угол поворота нормали представим в виде
, ,(7)
при аналогичных предположениях представим
.(8)
Таким образом, полученная система уравнений является замкнутой и в результате её интегрирования можно определить внутренние силы и перемещения 
и 
.
На основе гипотезы прямых нормалей перемещение произвольной точки оболочки (на расстояние z от срединной поверхности) с учетом осевых и цилиндрической жесткость стенки оболочки, изменениям угла поворота и максимальное деформации, возникающие в оболочке в связи с её изгибом представим в виде
, (i=1,2).(9)
В качестве физических уравнений принимаем соотношение нелинейной упругости
,
,(10)
где Е -модуль деформаций материала
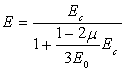,(11)
E0, 
– модуль упругости и коэффициент Пуассона для линейно упругого материала [1, с 26-29]; Ес – секущий модуль деформации.
Погонные усилия (рис.1) на единицу длины армированный оболочки относительно срединной поверхности определим зависимостями
, 
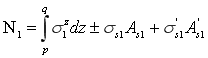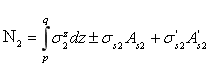.(12)
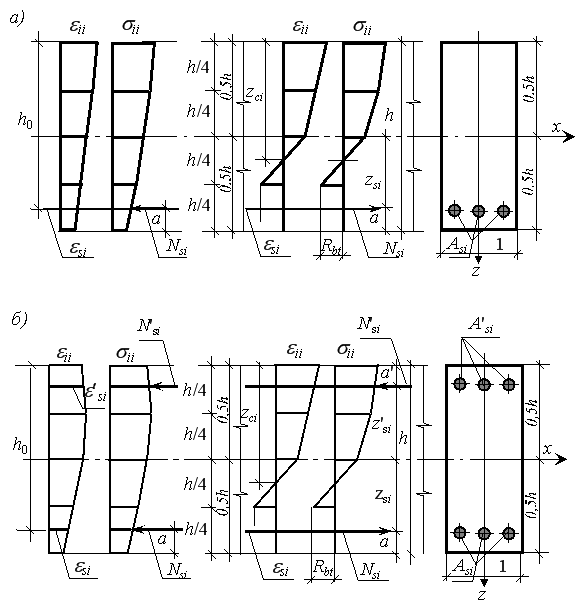
Рис 1. Эпюры деформаций и напряжений в поперечном сечении железобетонной оболочки с одиночной (а) и двойной (б) арматурой
Погонные моменты на единицу длины армированной оболочки определим зависимостями
,
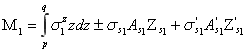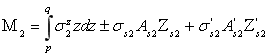.(13)
Пределы интегрирования приняты равными
или 
,
где 
–высота сжатой зоны сечения.
Высота сжатой зоны сечения 
определяется из геометрических соотношений (9) при 
на основе предложения В.М. Бондаренко [2, с 288] о совмещении нулевых деформаций и напряжений на единой нейтральной оси. Напряжения в арматуре 
и 
с учетом (9) представим
,
,
,(14)
.
Для случая одиночного армирования оболочки 
принимаются равными нулю.
Выражение для погонных усилий (12) с учетом (9)-(11), (14) после интегрирования в пределах p, qпредставим в виде
,
.(15)
здесь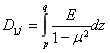 
; 
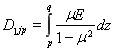
Моментные усилия (13), с учетом геометрических (9) и физических (10) зависимостей, представим следующими выражениями
,
.(16)
; 
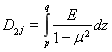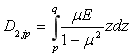;(j=1,2);
;
; 
;
;
; 
;(i=1,2),
здесь 
– прогиб оболочки с учетом начальных дефектов, допущенных при изготовлении
,
,
, 
, 
.
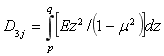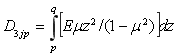Рассматривается случай больших oсесимметричных деформаций, в которых угол 
между нормалью и осью симметрии изменяется существенно, то есть уравнения равновесия составляется для деформированного состояния оболочки. Поэтому в отличие от рассмотренной линейной теории разница между углом 
для недеформированной и углом 
для деформированной оболочки будет существенной. В связи с этим вместо формул (7) и (8) и можно применят следующие формулы
,
, (17)
, 
.
Можно предположить, что радиальное перемещение
, согласно выражения
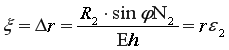
Уравнения равновесия оболочки при подстановке в них значений 
и кривизны деформированной оболочки
, 
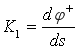принимают следующий вид
-
,
,(18)
.
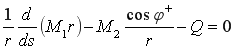В качестве основных искомых функций выбирают величины 
. Следует здесь отметить, что в отличие от линейного случая, где второй неизвестной был угол поворота 
, в нелинейном является полный угол нормали 
– для деформированный оболочки. Остальные неизвестные выражаются через основные в следующем виде
;
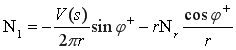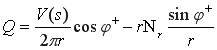;(19)
;
.
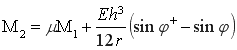Система уравнений (18) после некоторых преобразований с учетом (17) и (19) примет вид
;
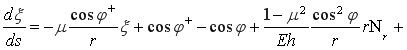
;(20)
;
.
К этой замкнутой системе четырех уравнений с четырьмя неизвестными следует добавить уравнение для определения осевых перемещений [3, с 83-85]
(21)
Если считать угол поворота нормали
малым, то в полученных уравнениях следует принять
, 
;(22)
если при этом сохранить только члены первого порядка малости, то уравнения совпадут с линейными. Так же как и в линейном случае, для уравнения (20) можно решить задачу Коши-Бидермана, т.е., зная значения основных неизвестных 
, параметров в начальном сечении оболочки s=so,можно определить, путем интегрирования уравнений на ЭВМ значения тех же неизвестных при s=s1 . При этом, как в линейной задаче, две из четырех величин для s=so находят из граничных условий, а остальные две выбирают так, чтобы удовлетворялось условие на торце s=s1.
Приведенная методика расчета также приемлема для оценки напряженно-деформированного состояния ребристых конических оболочек куполов при линейном и нелинейном деформировании с учетом моментных и безмоментных состояний.
Литература:
- ГОСТ 24452-80. Методы определения призменной прочности, модуля упругости и коэффициента Пуассона. М.: Госстандарт, 1981. – С. 26-29.
- Бондаренко В.М., Бондаренко С.В. Инженерные методы нелинейной теории железобетона. – М.: Стройиздат, 1982. -288 с.
- Бердиев О.Б. Определение модуля деформации бетона в конических оболочках при высоких уровнях загружения // Науч. тр. Республиканской научно-технической конференции с участием зарубежных ученых. – Ташкент, 2010. – С. 83-85.
