Распространение волн напряжения в плоскостях с свободными краями

Ядгаров Уктам Турсунович, кандидат технических наук, доцент

Бухарский инженерно-технологический институт (Узбекистан)

В работе рассматривается проблема распространения вынужденных импульсов напряжения в элементах плоскостей со свободными краями. Оно исходит из дифференциальных уравнений движения линейной теории упругости для плюской задачи:

(1)

где:

v- коэффициент Пуассона, Е- модуль упругости.

Поиск решения уравнения (1) сводится к следующему:

где: — круговая частота,

Подставляя (3) ва(1) получим следующее выражение:

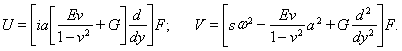(4)

Здесь F удовлетворяет дифференциальному уравнению четвертого порядка

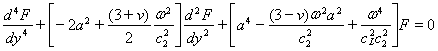
где:

Решение уравнения (4) выражается через экспоненциальных функций:

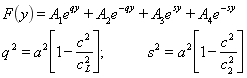(5)

При симметричном движении решение (5) примет вцд:

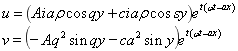(6)

На краях y=±e/2 ставится следующие граничные условия:

(7)

Подставляя (6) в (7) получим следующее дисперсионное уравнение:

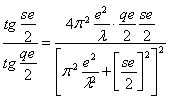(8)

где:

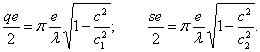
В таблице приведено изменение фазовой скорости (с/с0) от длины волны

Таблица

Если, из (8), полечим с=с0. В случае тогда (8):

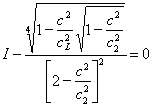
(8) в таком виде означает уравнение Рэле (1).

С помощью метода стационарной фазы Кельвина и метода анализа Фурье объясняются основные свойства распространения и деформирования широкополосных импульсов напряжения в полосе стены со свободными краями. Вычисление с помощью ЭВМ было проведено при наличии импульса напряжений в форме (х=0):

(9)

«В» и «а» характеризуют импульс, , или выражение (9) можно записать в виде:

или

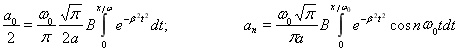
После некоторых преобразований можно найти перемещение полосы

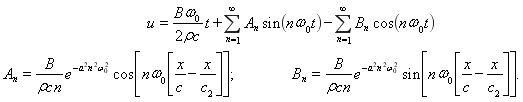
Результаты данных исследований показали, что имеет место существование геометрической дисперсии на распространение упругих волн напряжения. Помимо того, оно влияет на импульсов напряжения в плоских образцах, а также способствует боже глубокому объяснению ударных явлений.

Литература:

1. Сафаров И. И. «Колебания и волны в диссипативно неоднородных средах и конструкциях». — Ташкент, 1992.