В статье рассматривается импульсное взаимодействие плоского тела со стержневой упругой системой. Рассмотрен вопрос предотвращения кривизны возмущения упругой системы.
Импульсное взаимодействие систем связано с изменением энергии и в этой связи имеет сложную динамику, особенности которой определяются частными условиями.
Если на упругую стержневую систему действовать касательно плоским телом, расположенным перпендикулярно её продольной оси, способным обеспечить ей мгновенное приращение скорости ∆V, то этим можно создать значительные силы инерции. Эффект инерциального проявления возрастает пропорционально суммарной массе m свободной вершиной части системы. При выборе соответствующей геометрии взаимодействующей поверхности плоского тела можно предельно уменьшить действие точечного ударного процесса и явлений, связанных с ними, и привести к случаю скоростного касательного взаимодействия. Динамика процесса будет иметь более резкое проявление в случае наложения на основание системы различных связей, например, зажим стержней в подающем зажимном транспортере.
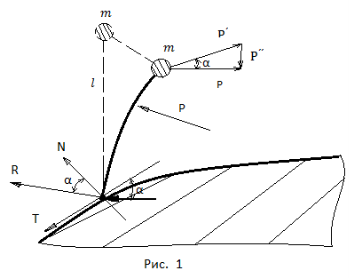
Сила инерции Р вершинной части стержней (рис. 1) после взаимодействия плоским телом
(1)
Где 
и 
- соответственно скорости транспортирования системы плоского тела.
Из уравнения (1) следует, что больший эффект действия силы Р возможен при и , противоположных по знаку (случай встречного движения), и условий, что ||>||. При касательном движении импульса со стороны плоского твердого тела упругая система будет испытывать действие двух характерных составляющих сил 
сил инерции Р.
Если угол касания α, то эти силы соответственно равны:
=Р/cosα; 
= tgα (2)
При этом сила направляет вершину стержней вдоль поверхности касания, другая наклоняет их на плоское тело. Если сила Р не превышает критических значений, скольжение системы вдоль грани касания должен существовать в пределе значений 0<α<П/2.
При α=const силы затухают пропорционально изучению функции ускорения. Это показательно для случая, когда грань тела образует прямая линия. Если же грань тела описать по некоторой кривой, то возможно возникновение дополнительных динамический явлений, зависящих от изменения функции ускорения тел скольжения.
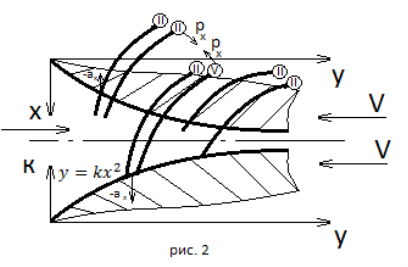
Если принять, как простейший и наиболее технологичный случай, когда образующая поверхности скольжения имеет вид 
и скорость движения упругой системы 
. Тогда движение вершинной части стрержнеивых элементов после импульса встречного взаимодействия относительно выбранной системы координат в параметрической форме (рис. 2) описывается системой:
(3)
C учетом приятных допущений следует, что ускорения стержневой массы относительно осей соответственно равны:
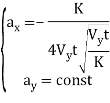(4)
Где 
- скорость стержневой системы относительно оси у; К- постоянная характеристика образующей кривой.
Из выражения (4) следует, что при выбранной форме поверхности касания возможно возникновение сил инерции, направленных противоположно ускорению 
и влияющих на поведение вершинной части массы упругих элементов, которые начнут двигаться вдоль оси Х в положительном направлении. Если стержневую систему обхватить одновременно двумя идентичными плоскими телами (рис. 2) при условии их встречного касания, то силовые импульсы в соответствии с уравнением (4) будут действовать встречно и создадут эффект бокового уплотнения системы элементов. Этим можно упорядочить движение упругой системы и обеспечить направленность ее движения в заходное щелевое пространство плоского тела, определяемого криволинейными образующими поверхности скольжения.
Движение системы вдоль грани щели возможно, если
(5)
Здесь N- нормальная реакция грани на действие силового импульса; f- коэффициент трения.
Из (рис. 1) видно, что 
. Тогда из условий (2) и (5) с учетом ограничений следует, что 
. Это означает, что заход стержневой системы в щелевое пространство возможен практически при всех условиях трения. С целью предотвращения повреждаемости поверхности следует ввести ограничение на угол касания, т. е. α<ϕ (ϕ- угол трения).
Стержневая система создает давление на грань плоского тела, равное реакции N, которая оценена выражением из условия упругой деформации
(6)
Где IE- жесткость упругой системы; p- радиус кривизны изогнутых стержней; l- Удаление точки касания от вершинной части.
Из выражения (6) следует, что трение при относительном движении плоского тела и стержней возрастает пропорционально значениям p и l. Поэтому для снижения сопротивления движения целесообразно обеспечить процесс взаимодействия плоского тела с системой упругих стержней в предельно нижнем положении. Предотвратить недопустимую кривизну возмущенной упругой системы можно либо установкой специальных упоров на поверхности плоского тела, либо заданием ему движения одновременно и вдоль продольной оси стержневой массы. Последнее условие, более доступное, можно обеспечить, если плоскому телу задать вторую кривизну, при которой возможно перемещение поверхности касания не только в перпендикулярном, но и в продольном направлении. Из анализа состояния системы при дополнительном возмущении следует, что движение плоского тела вдоль продольной оси возможно обеспечить при постоянстве скорости, не допуская её предельных значений. Этим исключается процесс захлестывания.
Описанные динамические явления могут быть положены в основу конструирования новых рабочих органов сельскохозяйственных машин, где в роли упругой системы может быть принята стебельная масса. Экспериментальная проверка на очесе стеблей льна щелевым очесывающим аппаратном подтверждает правильность сделанных выводов.
Литература:
- Фролов В. С. Инерциальная навигация.: Издательство «Знание» Москва 1970.-48с.
- Яблонский А. А. Курс теоретической механики.- М.: Высшая школа,1966
- Болотин Н. Н. Динамическая устойчивость упругих систем.-М.:Гостехиздат,1956
