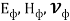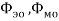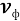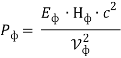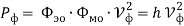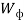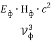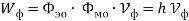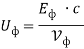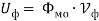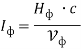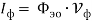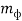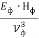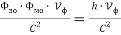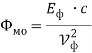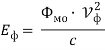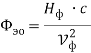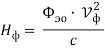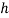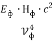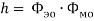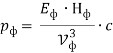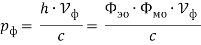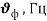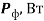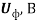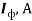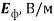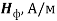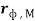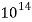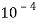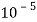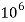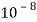Электромагнитные параметры единичных фотонов



В настоящей работе вводится ряд электромагнитных параметров единичных фотонов электромагнитного излучения и устанавливается связь с их квантовыми параметрами на основе метода аналогий [1] и метода анализа размерностей [2, с. 127–136].

Известно, что понятиями напряженности электрических и магнитных полей пользуются для описания световой волны в условиях классичности, когда число фотонов N 1 [3, с. 84-85]. Так как фотон является электромагнитным образованием, то его также, как и световую волну, можно характеризовать определенными значениями напряженности электрического поля фотона и напряженности магнитного поля фотона .

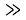
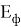
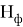
Согласно квантовой теории, электромагнитное излучение испускается или поглощается в виде порций энергии (квантов).

(1)

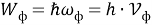
Где =

Дж∙с или

Дж∙с – постоянная Планка;

- циклическая частота фотона

– частота фотона

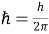
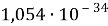
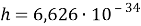
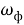
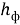
Воспользуемся методом анализа размерностей и запишем единицу измерения в следующем виде

[ (2)

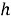
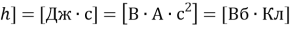
Как видно единицу измерения можно представить в виде произведения единицы измерения магнитного потока и единицы измерения электрического потока.

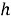
Так как элементарный электрический поток (квант электрического поля) имеет величину, равную =1,6∙ Кл, а элементарный магнитный поток (квант магнитного поля, соответствующей элементарному заряду) =4,14∙ Вб (4, то если взять произведение элементарных потоков, получим выражение

(3),

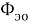
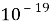
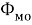
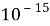
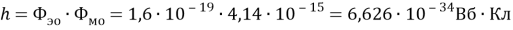
по численному значению, равное постоянной Планка.

Для фотона можно ввести понятие электромагнитной мощности

(4)

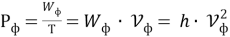
Где Т – период колебаний электромагнитного поля фотона с другой стороны выражение для мощности фотона можно записать в виде

= , тогда (5)

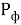
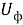
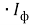
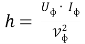
Где Uф, Iф – напряжение и ток, соответствующие электромагнитной мощности фотона.

Сравнивая для фотона выражение (3) и (5)

и

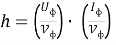
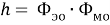
Получим для напряжения, тока и мощности фотона следующие зависимости

= ∙ ; (6)

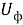
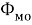
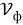
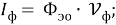
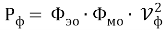
С другой стороны, эти величины можно выразить через напряженности электрических и магнитных полей

= (7)

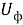
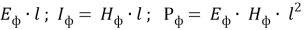
Где - граничные размеры фотона;

- радиус фотона

, – напряженности электрического и магнитного полей фотона.

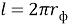
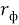
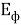
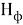
Граничные размеры фотона получим из выражения момента количества движения фотона [5, с. 79; 6, с. 317].

(8)

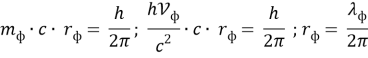
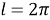
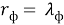
где - скорость света в вакууме

– длина волны фотона, м

– масса фотона, кг

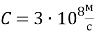
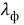
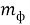
Проведя преобразования, получим следующие выражения для электромагнитных параметров фотона и их связи с квантовыми параметрами, которые сведены в таблицу 1.

Таблица 1

Название параметра	Формулы, выраженные через	Формулы выраженные через ,
Электромагнитная мощность фотона
Энергия фотона	=
Напряжение фотона
Ток фотона
Масса фотона	=	=
Квант магнитного поля
Напряженность электрического поля
Квант электрического поля
Напряженность магнитного поля
Постоянная	=
Импульс фотона

Таким образом, фотон можно характеризовать не только частотой колебаний, энергией, массой, импульсом, но и величинами напряженностей электрического и магнитного полей, электромагнитной мощностью, напряжением, током.

В таблице 2 приведены результаты расчетов электромагнитных параметров для фотонов фиолетового, зеленого и оранжевого видимого излучения.

Таблица 2

Частота	Электромагнитная мощность	Напряжение	Сила тока	Напряженность электрического поля	Напряженность магнитного поля	Радиус фотона
7,5∙ 6∙ 5∙	3,727∙ 2,385∙ 1,656∙	3,105 2,5 2,07	12∙ 9,6∙ 8∙	7,7625∙ 4,968∙ 3,45∙	300 192 133,3	6,4∙ 7,96∙ 9,55∙

Расчеты показывают, что фотоны различной частоты имеют разные линейные размеры и разные величины и . При этом, чем выше частота, тем меньше линейные размеры фотона и тем больше величины , , .

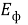
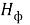
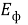
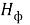
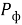
Литература:

1. Гомоюнов К.К Совершенствование преподавания технических дисциплин. -Л: Издательство Ленинградского университета, 1983, 206с
2. Бутиков Е.И, Быков А.А., Кондратьев А.С. Пособие по физике. - М: ООО «Издательство Мир и Образование, 2004, 640с
3. Тарасов Л.В Введение в квантовую оптику. М: Высшая школа, 1987, 304с
4. Яворский Б.М., Детлаф А.А. Справочник по физике. – М: Наука, Главный редактор физико-математической литературы, 1981, 512с
5. Королев Ф.А. Теоретическая оптика. – М: Высшая школа 1966, 596с
6. Хайкин С.Э. Физические основы механики, Нос издательство физико-математической литературы. - М. 1962, 772с