Ионное распыление было открыто в 1852 году В. Р. Гроувом. Распыление — это удаление поверхностных атомов при бомбардировке твёрдого тела ускоренными частицами, происходящее при столкновении частиц и атомов тела в приповерхностных слоях. После столкновения некоторые атомы, находящиеся в граничном слое, приобретают энергию, достаточную для вылета с поверхности тела (рис. 1).
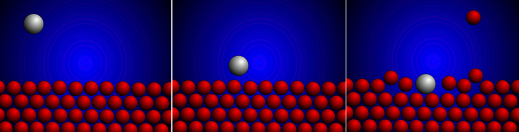
Рис. 1. Падающий ион, падающий на поверхность твердого тела, вызывает каскад столкновений, что приводит к эмиссии его атомов
Идея последовательных фокусированных столкновений — фокусонов — была впервые предложена в 1957 г. Р. Силсби [1]. Фокусоны передают импульс неподвижным атомам плотноупакованной цепочки, так, что он распространяется под углом θ к оси цепочки, меньшим при каждом следующем столкновении.
Изучение фокусировки атомных столкновений очень важно для изучения радиационных возмущений и для изучения катодного распыления. Также изучение распыления поверхностей под действием быстрых частиц имеет особое значение, в частности, в связи с запуском искусственных спутников Земли и космических кораблей, корпус которых бомбардируется частицами в верхних слоях атмосферы и в межпланетном пространстве [2]. Немаловажны и закономерности разрушения металлов в результате ионной бомбардировки при конструировании плазменных и ионных двигателей для космических кораблей. Изучение механизма распыления металлов под действием ионов, имеющих относительно высокую энергию, актуально из-за влияния этого процесса на загрязнение плазмы в термоядерных установках. Также изучение фокусировки атомных столкновений важно для анализа и очистки различных поверхностей, создания наноструктур, пор или другого рельефа, исследования дефектов поверхностей в полупроводниках.
Рассмотрение, проведенное Силсби, показывает, что при r (диаметр шара), близких по величине к D (расстояние между шарами), и при малых D движущаяся частица передает свой импульс неподвижным атомам плотноупакованной цепочки, так, что он распространяется под углом θ к оси цепочки, меньшим при каждом следующем столкновении.
Влияние регулярного расположения атомов в кристаллической решетке твердых тел приводит к тому, что при бомбардировке заряженными или нейтральными частицами преобладает распространение волны столкновений атомов вдоль направлений наиболее плотной упаковки решетки [3].
В 1955 году Венер озвучил идею, что ион, ударяющий твёрдое тело, передает свой импульс атомам плотноупакованной цепочки распыляемого кристалла, вследствие чего на коллекторе вблизи распыляемого образца образуется осадок в виде симметричных пятен — «пятен Венера» (рис. 2) [4].
По предположению Р. Силсби, картина пятен при эмиссии атомов с поверхности кристалла обусловлена распространением фокусированных цепочек атомных столкновений, но в 1966 году К. Леман, П. Зигмунд и Д.Харрисон показали, что роль фокусонов в механизме распыления не всегда достаточно значительна как при малых, так и высоких энергиях бомбардировки, и что «пятна Венера» могут быть причиной упорядоченного расположения атомов лишь двух приповерхностных атомных слоёв кристалла [5, 6].
Р.Нельсон и М.Томпсон наблюдали распределение осадка в виде симметричных пятен при распылении поликристаллических мишеней, что объяснялось как результат фокусировки импульса линзами из нескольких атомов [7].
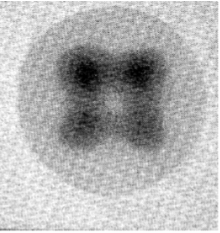
Рис. 2. Пятна Венера, обнаруженные при бомбардировке поверхности Ag ионами Hg + с энергией 100 эВ
Постановка задачи . Р. Силсби впервые указал, что в плотноупакованной изолированной цепочке равноотстоящих атомов при определенных условиях может происходить фокусировка удара. Рассмотрим одномерную цепочку из большого числа атомов на расстоянии D друг от друга, которые мы будем считать жесткими шарами с диаметром r . Сообщим крайнему шару скорость v 0 под углом θ 0 к цепочке (рис.3).
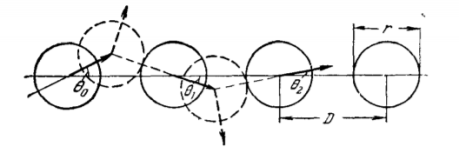
Рис. 3. Фокусирующий эффект при распространении удара вдоль линейной цепочки жестких шаров
Из закона сохранения импульса и энергии следуют рекуррентные соотношения, где θ n — угол между вектором скорости n -го шара и направлением цепочки, α = D / r , E n — кинетическая энергия, которая передается при столкновении:
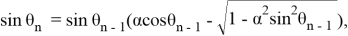
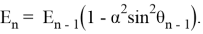
Применяя приближение малых углов, получаем:
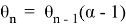
Отношение
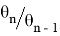
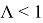
Итак, для параметра фокусировки получаем соотношение:
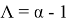
Таким образом, образование фокусонов (по крайней мере, при малых углах столкновения) возможно при
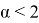
Критический угол образования фокусона . Найдем максимальный начальный угол, при котором столкновение все еще возможно (оно будет касательным). Так как скорость v 0 направлена по касательной (рис. 4), то получившийся треугольник будет прямоугольным. Из него мы находим:
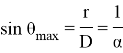
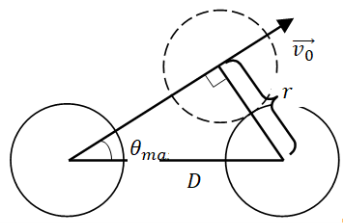
Рис. 4. К расчету максимального начального угла
Отметим, что при
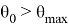
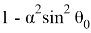
Теперь определим критический угол
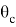
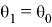
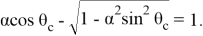
Уединим корень и возведем в квадрат:
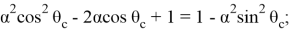
после использования основного тригонометрического тождества получим
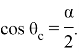
Так как косинус любого угла не может превосходить единицы, получаем ограничение на
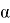
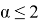
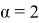
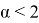
Энергия фокусировки.
Рассмотрим цепочку из очень большого количества атомов. Значение энергии, которая будет передана от первого атома к последнему, может быть найдена путем «разворачивания» рекуррентных соотношений и последующим предельным переходом
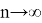
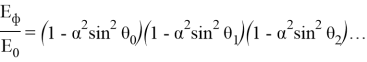
Применим приближение малых углов и раскроем скобки, оставляя только слагаемые вида
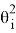
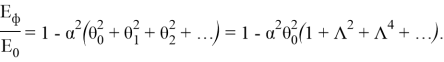
В скобках стоит сумма бесконечно убывающей геометрической прогрессии со знаменателем
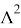
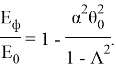
Итак, мы получили очень осмысленное выражение, поскольку дробь в правой части характеризует долю энергии, потерянной в цепочке столкновений.
Методика исследования
. В данной задаче используется программа Focuson (рис. 5), которая была написана на языке программирования Object Pascal с использованием среды программирования Borland Delphi 7. В процессе выполнения программы происходит моделирование и визуализация столкновений шаров. Основными элементами окна программы являются панель ввода данных и область моделирования. В соответствующие поля на панели вводятся количество частиц (от 2 до 10), начальный угол
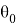
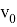
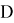
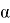
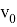
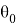
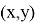
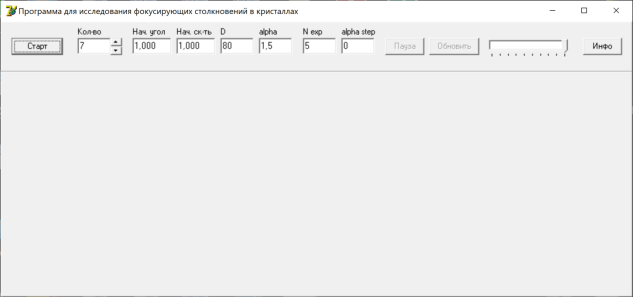
Рис. 5. Скриншот программы
На каждом временном шаге выполняется сдвиг шаров:
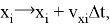
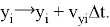
Если i-ый и j-ый шар сближаются на расстояние
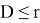
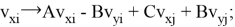
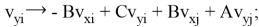
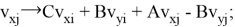
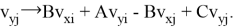
Коэффициенты
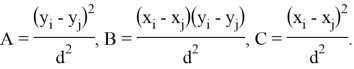
После каждого соударения рассчитываются
Результаты и
обсуждение
. При
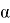
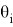
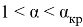
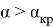
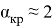
Методом подбора был определен критический начальный угол
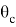
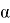
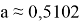
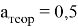
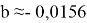
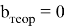
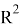
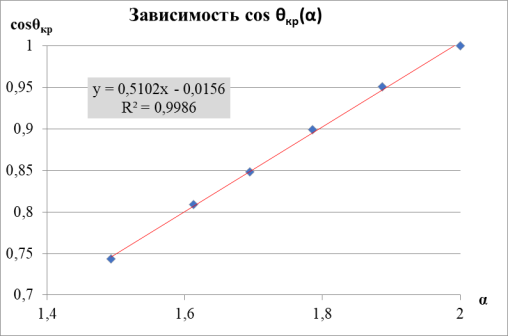
Рис. 6. Зависимость
Для начального угла
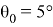
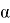
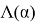
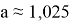
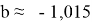
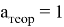
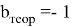
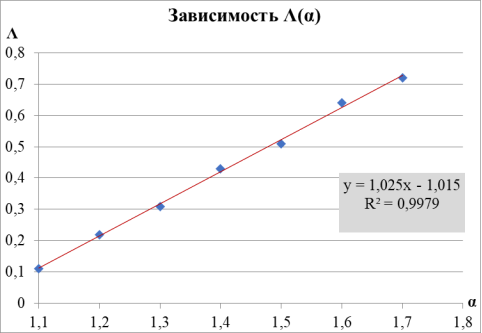
Рис. 7: Зависимость параметра фокусировки от
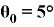
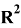
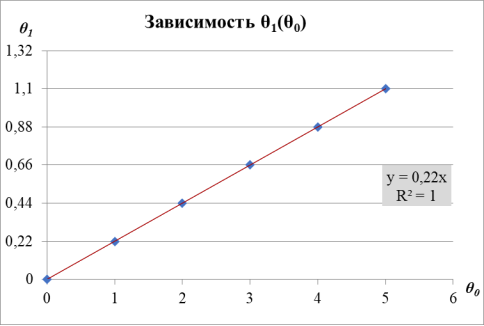
Рис. 8. Зависимость
θ
1
от
θ
0
.
Указаны коэффициенты линейной зависимости и величина достоверности
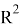
При
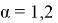
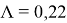
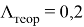
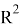
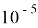
При θ
0
= 5
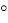
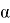
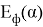
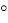
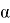
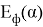
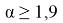
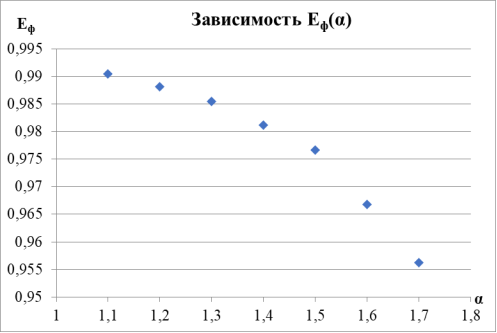
Рис. 9. Зависимость энергии фокусировки от
α
. Указаны коэффициенты линейной зависимости и величина достоверности
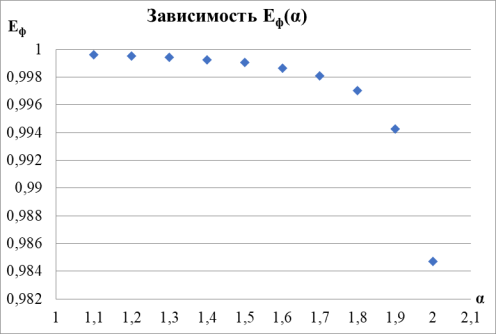
Рис. 10. Зависимость энергии фокусировки от
α
. Указаны коэффициенты линейной зависимости и величина достоверности
Выводы . Нами был создан программный продукт, позволяющий исследовать фокусировку столкновений в цепочке атомов. С использованием численной модели была проверена фокусонная модель Р. Силсби [1]. Результаты хорошо согласуются.
Результаты работы могут быть полезны для понимания процессов атомных столкновений, которые важны для анализа и очистки поверхности, создания наноструктур или какого-либо рельефа, для исследования дефектов в полупроводниках, а также для изучения закономерности разрушения металлов в результате ионной бомбардировки при конструировании плазменных и ионных двигателей для космических кораблей. Ещё их можно будет использовать для объяснения пятен Венера при распылении монокристаллов.
Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М. В. Ломоносова [8].
Результаты работы в 2019–2020 учебном году были представлены на следующих конференциях:
– XXIX Открытая московская инженерная конференция школьников «Потенциал» (Москва, 31 января — 1 февраля 2020 г.)
– Всероссийский конкурс научных работ школьников «Юниор» (Москва, 31 января — 2 февраля 2020 г.)
– Конференция «Наука для жизни» (Москва, 1–10 апреля 2020 г.)
– Конференция «Курчатовский проект — от знаний к практике, от практики к результату» (Москва, 13–15 апреля 2020 г.)
На конференции «Потенциал» доклад занял II место в секции «Физика».
Работа выполнена на базе ГБОУ Школа № 1557 имени Петра Леонидовича Капицы в рамках проекта «Курчатовский проект в московской школе» совместно с лабораторией «Теоретические исследования процессов на поверхности кристаллов» МГУ им. М. В. Ломоносова. Авторы благодарят доцента кафедры общей физики физического факультета МГУ Самойлова В. Н. за неоценимый научный вклад и за обсуждение результатов, а также администрацию ГБОУ Школа № 1557 за помощь и поддержку.
Литература:
1. R. H. Silsbee, Focusing in Collision Problems in Solids. // Journal of Applied Physics. 28, 1246 (1957).
2. D. ΜсКеоwn, New Method for Measuring Sputtering in the Region Near Threshold // Review of Scientific Instruments. 32(2), 133–136, (1961).
3. Р. И. Гарбер, А. И. Федоренко. Фокусировка атомных столкновений в кристаллах // Успехи физических наук (1964).
4. G. K. Wehner, Sputtering of Metal Single Crystals by Ion Bombardment // Journal of Applied Physics. 26(8), 1056–1057 (1955).
5. Lehmann, Chr., Sigmund P. On the Mechanism of Sputtering. // Phys. Stat. Sol. 1966. V. 16. No. 2. P. 507–511.
6. Harrison D. E., Johnson J. P., Levy N. S. Spot patterns and Silsbee chains of a Cu single crystal // Appl. Phys. Lett. 1966 V. 8 No. 2 P. 33–36.
7. Nelson R. S., Thompson M. W. Atomic collision sequences in crystals of copper, silver and gold revealed by sputtering in energetic ion beams // Proc. Roy. Soc. 1961 V. A259. No. 1299 P. 458–479.
8. Воеводин Вл.В., Жуматий С. А., Соболев С. И., Антонов А. С., Брызгалов П. А., Никитенко Д. А., Стефанов К. С., Воеводин Вад.В. Практика суперкомпьютера «Ломоносов» // Открытые системы. — Москва: Издательский дом «Открытые системы», N 7, 2012. С. 36–39.

