Интегродифференциальное уравнение Фредгольма



В работе рассматриваются следующие задачи:

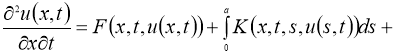
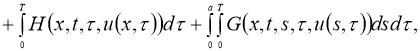
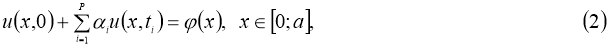
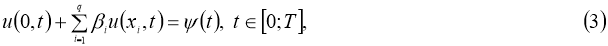
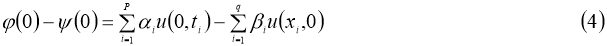
где

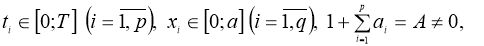
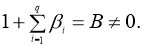
1. Однозначная разрешимость

В этом пункте находятся достаточные условия однозначной разрешимости задачи .

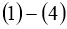
В пространстве используется норма

.

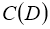
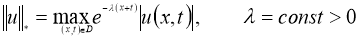
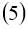
Теорема 1. Пусть непрерывные функции,

удовлетворяют условию:

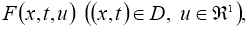
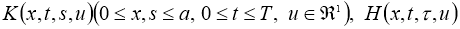
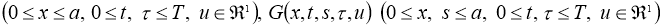
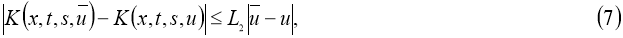
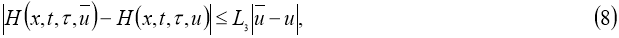
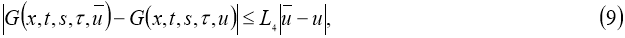
где

,

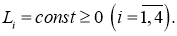
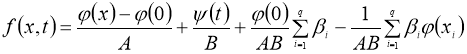
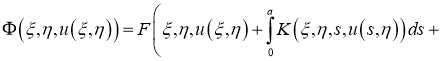
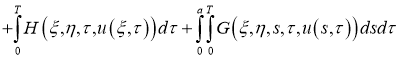
Если существует удовлетворяющая неравенству

, тогда задача имеет единственное решение в пространстве .

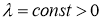
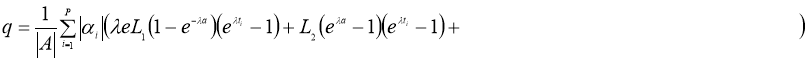
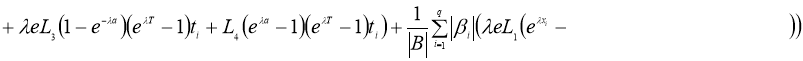
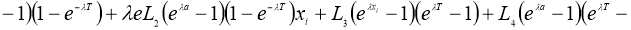
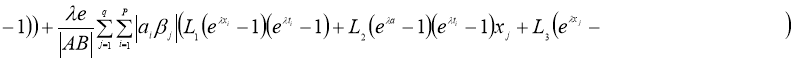
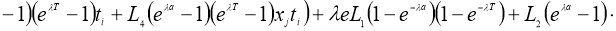
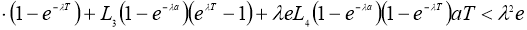
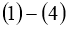
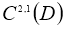
Доказательство.

Очевидно, что задача (1) — (4) эквивалентна интегрофункциональному уравнению:

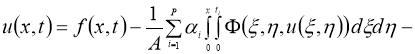
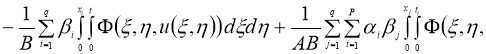
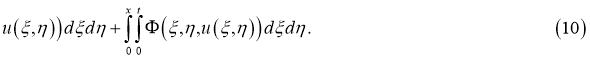
Пусть

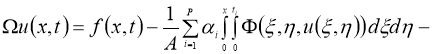
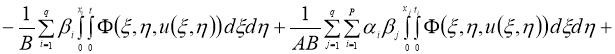
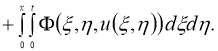
Очевидно, что . Теперь докажем, что оператор сжимающий. имеем:

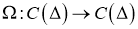
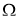
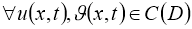
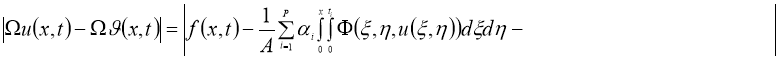
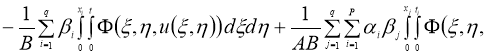
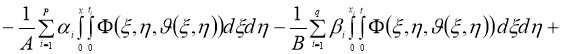
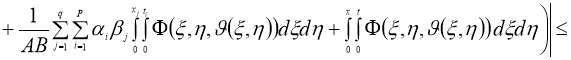
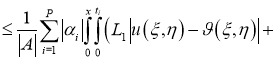
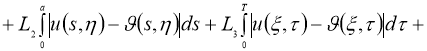
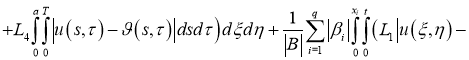
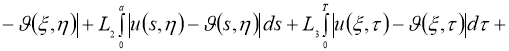
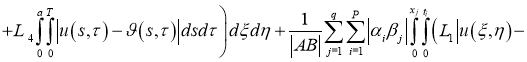
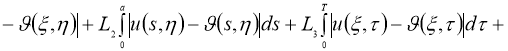
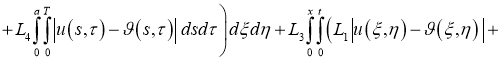
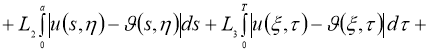
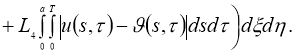
Используя норму (5), имеем:

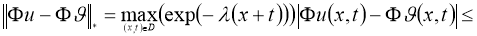
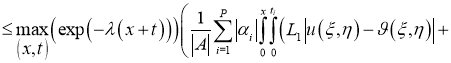
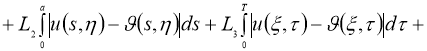
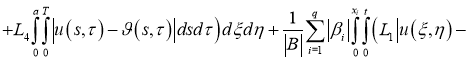
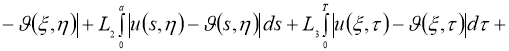
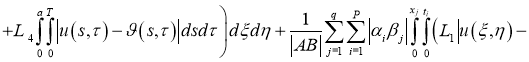
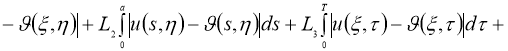
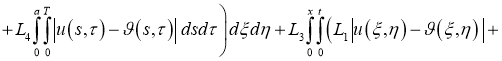
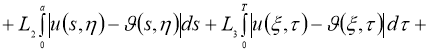
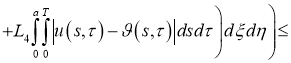
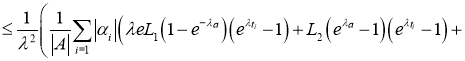
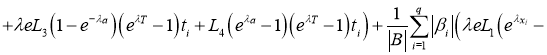
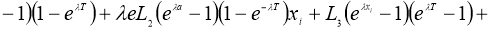
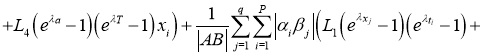
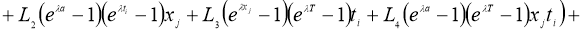
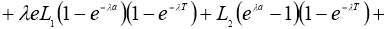
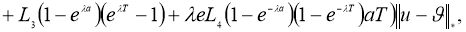
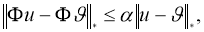
где Доказательство теоремы 1 следует из принципа сжимающих отображений.

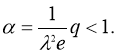
2. Непрерывная зависимость решения от параметров

Следующая задача:

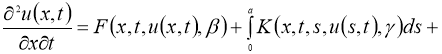
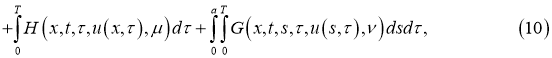
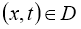
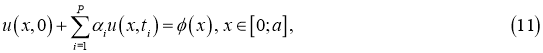
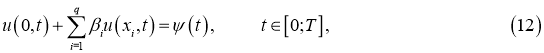
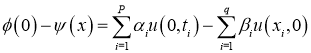
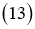
где

параметр.

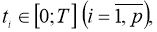
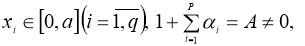
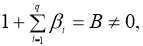
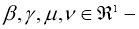
Теорема 2. Пусть, непрерывные функции

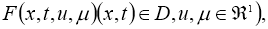
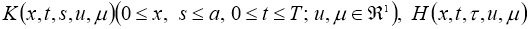
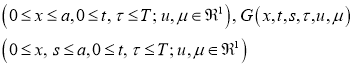
удовлетворяют условию:

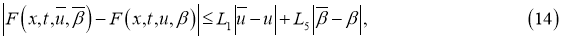
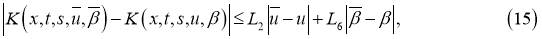
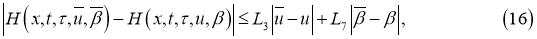
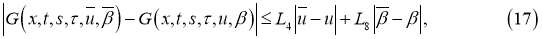
где

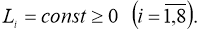
Если существует , удовлетворяющая неравенству

, тогда единственное решение задачи (1) — (4) непрерывно зависит от параметров.

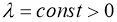
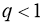
Доказательство. При фиксированных параметрах однозначной разрешимости задача доказана в теореме 1.

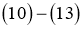
Задача эквивалентна следующему интегральному уравнению:

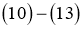
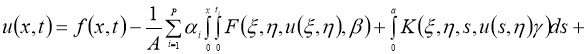
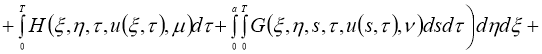
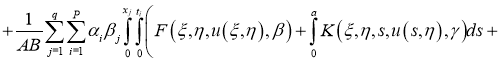
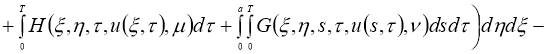
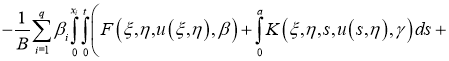
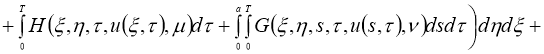
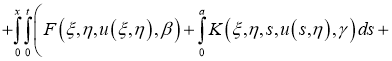
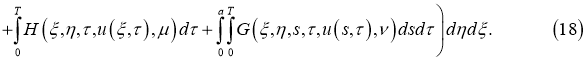
Обозначим через

решение уравнение , соответствующее параметрам и . Имеем

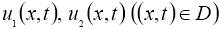
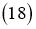
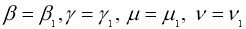
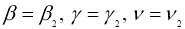
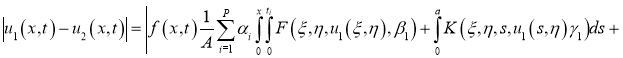
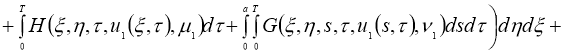
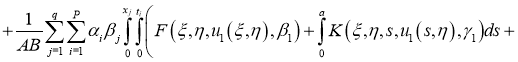
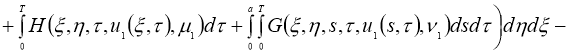
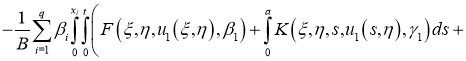
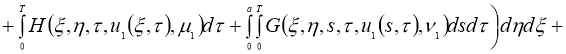
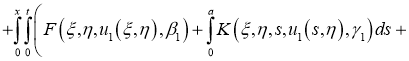
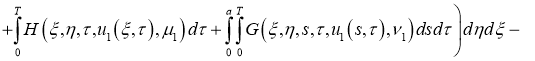
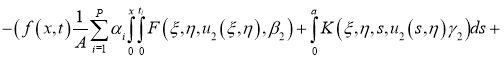
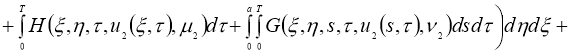
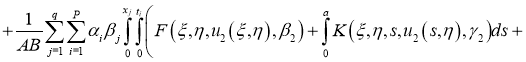
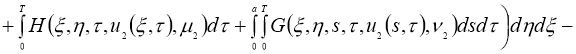
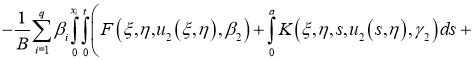
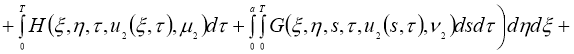
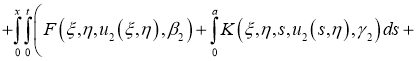
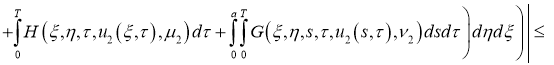
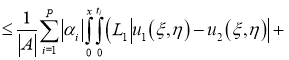
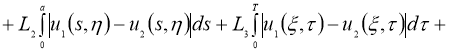
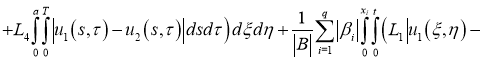
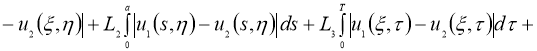
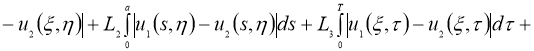
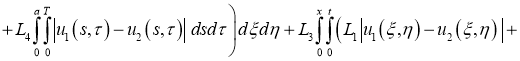
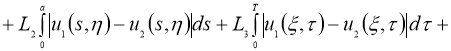
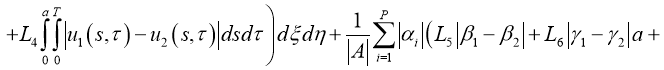
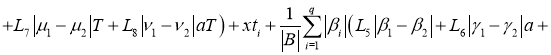
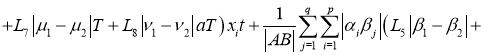
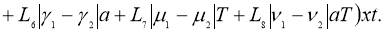
Имеем:

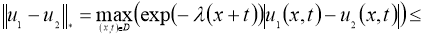
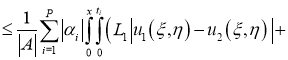
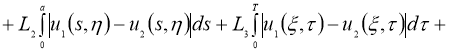
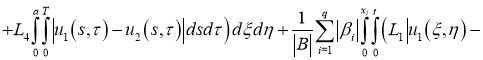
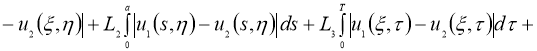
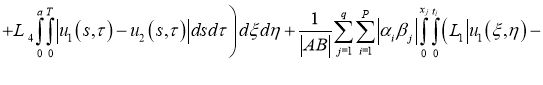
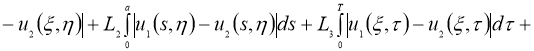
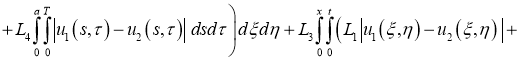
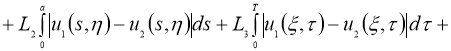
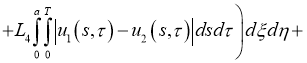
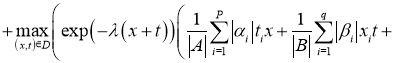
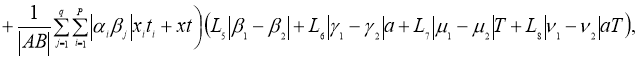
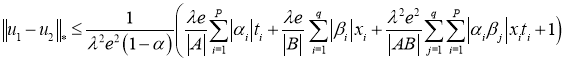
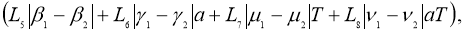
Отсюда следует утверждение теоремы 2.