Изучение теплофизических процессов, происходящих в электрических контактах, является весьма актуальным в автоматике. При математическом моделировании теплофизических свойств таких процессов возникает необходимость решения краевых задач теплопроводности, особенность которых состоит в наличии подвижной границы и вырождении области решения в начальный момент времени [1–3]. С помощью тепловых потенциалов решение таких задач сводится к решению особых интегральных уравнений Вольтерра второго рода. Особенность такого рода уравнений заключается в том, что норма интегрального оператора в классе существенно ограниченных функций равна единице, то есть к ним не применим метод последовательных приближений.
Рассмотрим интегральное уравнение
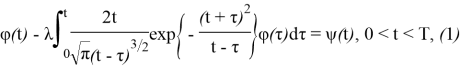
где
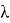

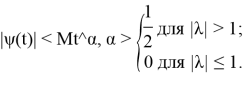
Подобного рода интегральные уравнения были предметом исследования в работах [4–7].
Решение уравнения (1) будем искать в классе функций
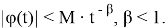
Легко видеть, что
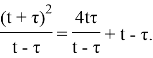
Ввиду этого уравнение (1) преобразуется к виду
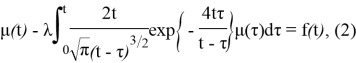
где
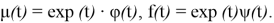
Рассмотрим однородное уравнение
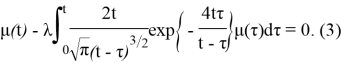
После применения преобразования Лапласа будем иметь
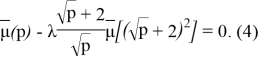
Решение этого функционального уравнения ищем в виде
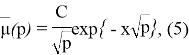
где
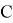
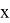
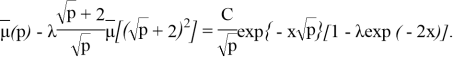
Выберем х так, чтобы выполнилось условие
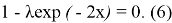
Корнями уравнения (6) являются
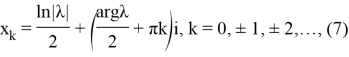
Полное решение уравнения (4) будем искать в виде
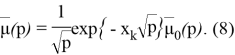
Подставляя (8) в (4), получим
Пусть
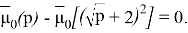
Тогда
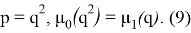
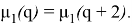
т. е.
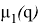
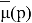
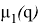
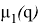
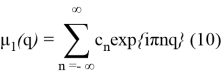
где
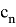
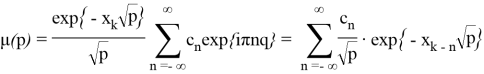
или
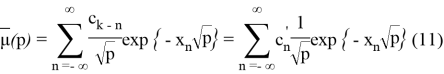
Для того, чтобы
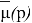
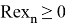

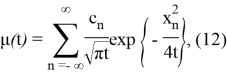
где
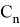
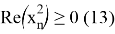
или
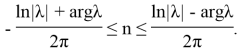
Пусть
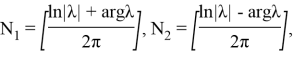
где
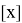
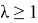
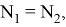

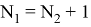
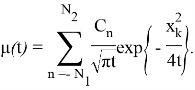
Если
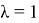
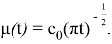
Если
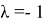
Теорема. Если
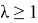
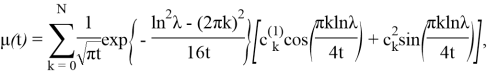
где
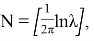
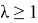
Если
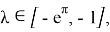
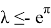
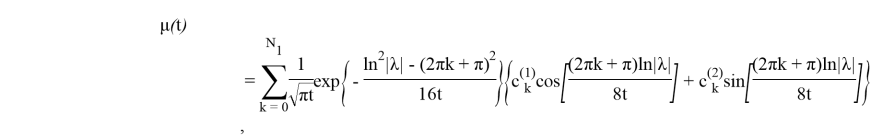
где
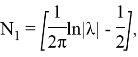
т. е. для каждого
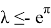
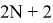
Рассмотрим неоднородные уравнение
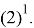
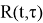
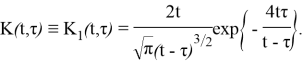
Очевидно, что
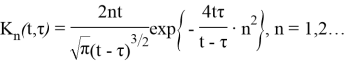
Тогда
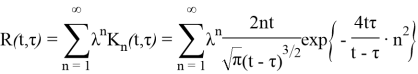
Запишем решение уравнения (2) формально в виде
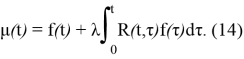
Если
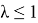
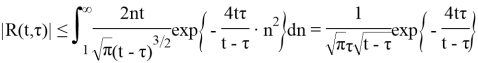
Таким образом, интеграл в (14) сходится при
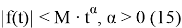
и, следовательно, к уравнению (2) можем применить метод последовательных приближений.
Если
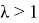
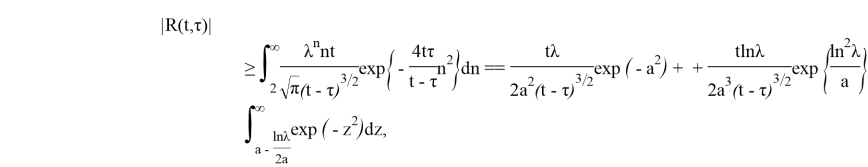
где
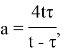
т. е.
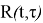
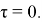
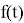
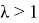
Предлагается другой метод. Произведем следующую замену:
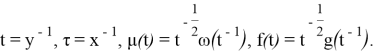
Тогда уравнение (2) примет вид
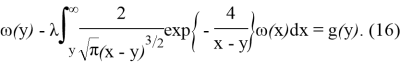
Предположим, что g(y) определена в
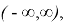
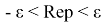
Пусть
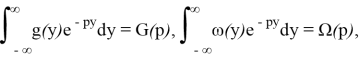
тогда
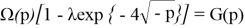
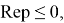
Отсюда
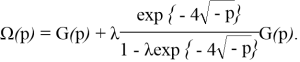
Найдем оригинал по формуле обращения:
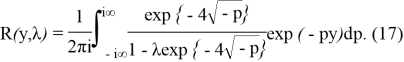
Если корни уравнения
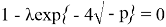
лежат на мнимой оси, т. е.
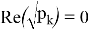
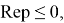
Из (18) очевидно, что
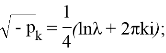
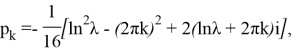
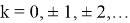
Значения R(y;λ) для
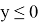
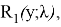
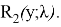
Пусть
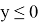
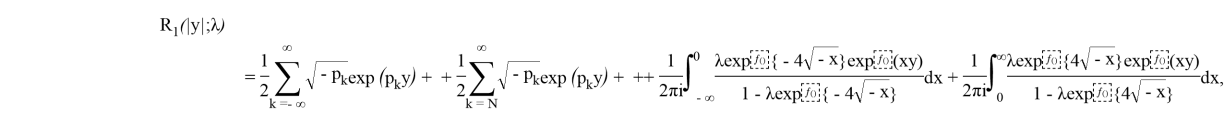
где
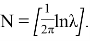
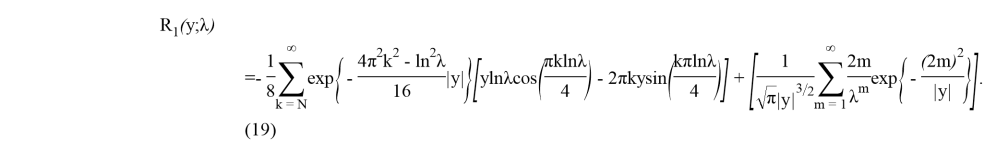
Пусть теперь
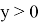
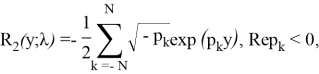
где
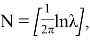
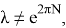
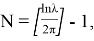
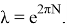
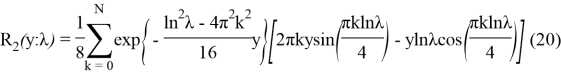
Окончательно частное решение уравнения (16) получается по формуле свертки
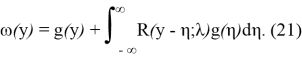
Для того, чтобы такое представление было возможным, доопределим функцию
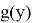
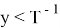
Если
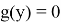
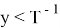
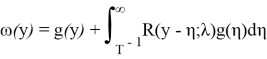
или
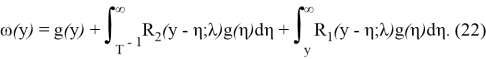
Чтобы определить класс функций
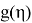
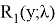
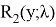
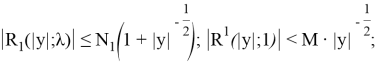
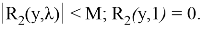
Итак, если
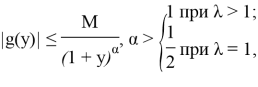
то интегралы в формуле (22) сходятся и функция
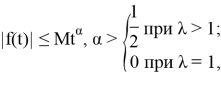
то
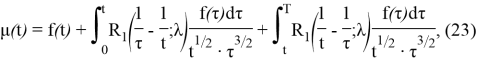
удовлетворяет уравнению (2).
Из п. I мы видим, что однородное уравнение (2) может иметь собственные функции для любого
Литература:
- Ким Е. И., Омельченко В. Т., Харин С. Н. Решение уравнения теплопроводности с разрывными коэффициентами н его приложение к вопросу электрических контактов. — ИФЖ, 1965, № 5.
- Харин С. Н. Тепловые процессы в электрических контактах и связанные с ними сингулярные интегральные уравнения. — Автореф. на соиск. ученой степени канд. наук. Алма-Ата, 1970.
- Ramazanov M. I., Gulmanov N. K. Solution of a two-dimensional boundary value problem of heat conduction in a degenerating domain // Journal of Mathematics, Mechanics and Computer Science. — 2021. — V.111, no.3. — P. 65–78.
- Михайлов Л. Г. Интегральные уравнения с ядром, однородным степени — 1. Душанбе, «Дониш», 1966.
- Бильман Б. М. Об интегральных уравнениях с переменными пределами интегрирования, ядра которых имеют особенность однородной функции степени-1.- В кн: дифференциальные и интегральные уравнения с сингулярными коэффициентами. Душанбе, «Дониш»,1969.
- Омаров Т. Е., Отелбаев М. О. Об одном классе сингулярных интегральных уравнений типа Вольтерра. -В кн.: Дифференциальные уравнения и их приложения. Алма-Ата, «Наука» КазССР, 1975.
- Рамазанов М. И., Гульманов Н. К. О сингулярном интегральном уравнении Вольтерра краевой задачи теплопроводности в вырождающейся области // Вестник Удмуртского университета. Математика. Механика. Компьютерные науки. — 2021. — Т.31. Вып. 2. — С.241–252.

