В прямоугольной области![]() изучается краевая задача для модельного уравнения второго порядка
изучается краевая задача для модельного уравнения второго порядка
![]() (1)
(1)
где
![]() и
и ![]() ,
,
![]() и
и ![]() ,
,
![]() .
.
Пусть ![]() ,
, ![]() ,
, ![]() вектор внутренней нормали к границе
вектор внутренней нормали к границе ![]() области
области ![]() ,
, ![]() . Заметим, что уравнение (1) в
. Заметим, что уравнение (1) в ![]() области является уравнением смешанного типа. А именно в
области является уравнением смешанного типа. А именно в ![]() оно будет гиперболо-параболическим, в
оно будет гиперболо-параболическим, в ![]() эллиптико-параболическим, прямая
эллиптико-параболическим, прямая ![]() есть линия вырождения типа уравнения.
есть линия вырождения типа уравнения.
Краевая задача: Найти в области ![]() решение уравнение (1) условие:
решение уравнение (1) условие:
![]() (2)
(2)
Численное решение краевой задачи (1)-(2) является непростой задачей ввиду того, что для нее не построена устойчивая разностная схема. В настоящей работе предлагается конструктивный подход построения устойчивой разностной схемы. При построении разностной схемы учитывается тип уравнения, т. е. строится гибридная схема.
С помощью функционального подхода в работе [1] доказана следующая теорема:
Теорема1. Пусть выполнены условия
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() в окрестности точек
в окрестности точек ![]() и
и ![]() , кроме того,
, кроме того, ![]() вдоль характеристики. Тогда если решение задачи (1)-(2) их пространства
вдоль характеристики. Тогда если решение задачи (1)-(2) их пространства ![]() существует, то оно единственно. Здесь через
существует, то оно единственно. Здесь через ![]() обозначено пространство Соболева с весом, которое получается замыканием класса дважды непрерывно дифференцируемых в
обозначено пространство Соболева с весом, которое получается замыканием класса дважды непрерывно дифференцируемых в ![]() функций, удовлетворяющих условию (2) по норме:
функций, удовлетворяющих условию (2) по норме:
![]() .
.
Разностная схема. Схему будем строить отдельно в области ![]() и отдельно в области
и отдельно в области ![]() . С этой целью в области
. С этой целью в области ![]() строим разностную сетку,
строим разностную сетку, ![]() . Здесь
. Здесь ![]() — шаг по
— шаг по ![]() , а
, а ![]() — шаг по
— шаг по ![]() .
.
Введем в рассмотрение следующие обозначения:
![]() ,
, ![]() ,
, ![]() — операторы сдвига:
— операторы сдвига: ![]()
![]() ,
, ![]() ,
,
а также ![]() — разностные операторы:
— разностные операторы: ![]()
![]()
![]()
![]() .
.
С помощью этих обозначений в области ![]() предлагаем следующую разностную схему:
предлагаем следующую разностную схему:
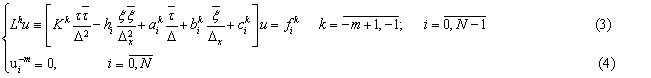
Разностная схема (3)-(4) является незамкнутой. Для нее требуется задание так называемого дополнительного граничного и начального условия. Для простоты мы предлагаем следующие дополнительные начальные и граничные условия:
![]() ,
, ![]() (5)
(5)
![]() ,
, ![]() ,
, ![]() (6)
(6)
Система линейных алгебраических уравнений (3)-(6) относительно неизвестных ![]() — образует полную систему. Для разностной схеме верна следующая оценка:
— образует полную систему. Для разностной схеме верна следующая оценка:
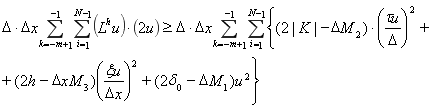 (7)
(7)
Шаги разностной сетки выбираем из условия:
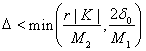 и
и ![]() ,
, ![]() ;
; ![]() (8)
(8)
Тогда если ![]() , то
, то ![]() , при
, при ![]() ,
, ![]() .
.
Таким образом, энергетическая оценка (7) при условии (7) обеспечивает однозначную разрешимость и устойчивость разностной схемы (3) –(6) в области ![]() .
.
Разностную схему исследуем в области ![]() . Поскольку уравнение (1) в области
. Поскольку уравнение (1) в области ![]() является гиперболо-параболическим, применяем следующий подход. Заменим уравнение (1) в области
является гиперболо-параболическим, применяем следующий подход. Заменим уравнение (1) в области ![]() эквивалентной ему симметрической системой первого порядка:
эквивалентной ему симметрической системой первого порядка:
![]() ,
, ![]() ,
, ![]() (9)
(9)
где 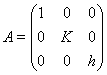 ,
, 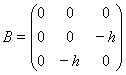 ,
, 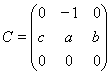 ,
, 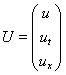 ,
, 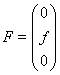
условием при ![]() (если
(если ![]() )
)
![]() ,
, ![]() ,
, ![]() (10)
(10)
Для задачи (9)-(10) легко можно получить априорную оценку:
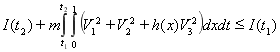 ,
, ![]()
где 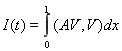 ,
, ![]() ,
, ![]() — некоторые постоянные.
— некоторые постоянные.
В частности при ![]() ,
, ![]() имеем
имеем ![]() и
и 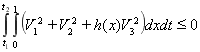
откуда следует ![]() и следовательно
и следовательно ![]() ,
, ![]() в области
в области ![]() . Это дает нам возможность легко применить разностные схемы, предложенные в работе [2] для численного решения уравнения (1) в области
. Это дает нам возможность легко применить разностные схемы, предложенные в работе [2] для численного решения уравнения (1) в области ![]() и получить энергетические оценки типа (8).
и получить энергетические оценки типа (8).
Литература:
- Рахмонов Х. О. О первой краевой задаче для одного уравнения смешанного типа в пространстве. — Новосибирск, 1985. -22с. (Препринт/ АН СССР, сиб.отд. ИМ, N-12).
- Алаев Р. Д. Метод диссипативных интегралов энергии для разностных схем. Изд-во Новосибирского университета, 1993, 68 с.

