Метод матрицы переноса в полупроводниках



В этой статье мы рассмотрим способ вычисления волновых функций в слоистых наноструктурах со ступенчатым потенциалом, называемый методом матриц переноса.

Ключевые слова: волновая функция, обратная матрица, ступенчатый потенциал, матрица переноса.

Основу этого метода составляет матричное описание условий сшивания волновых функций и их первых производных на границах слоев. Условия сшивания представляют собой линейные соотношения между парами коэффициентов А и B в волновых функциях вида или , относящихся к соседним слоям, так что их можно рассматривать как результат линейного преобразования двухкомпонентного вектор-столбца (A, B) некоторой матрицей формата 2×2. При этом связь между вектор столбцами двух крайних слоев в многослойной наноструктуре будет описываться произведением t-матриц (матриц переноса), отвечающих заданной последовательности промежуточных слоев. Метод матриц переноса особенно удобен в компьютерных программах, так как современные математические пакеты содержат встроенные подпрограммы для операций с матрицами и комплексными величинами, позволяя нам избежать громоздкого перемножения матриц вручную.

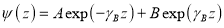
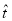
Условимся выбирать координатную ось z в направлении, перпендикулярном плоскости слоев, и будем нумеровать слои слева направо, как показано на рис. 1.

В рис.1 а — соответствие между картиной ступенчатого потенциала U(z), номерами слоев и граничными значениями zn в гетероструктуре с числом слоев N; б — стрелками изображены потоки падающих, прошедших и отразившихся частиц с энергией E в области континуума. Падающий поток задается произвольным коэффициентом А1. Отраженный и прошедший потоки можно найти, вычислив, соответственно, коэффициенты Bi и AN при условии BN = 0. в — в области размерно-квантованных состояний волновая функция имеет «хвосты» (схематично изображены пунктирными кривыми), убывающие в глубь крайних слоев, что соответствует условиям А1 = 0, BN = 0.

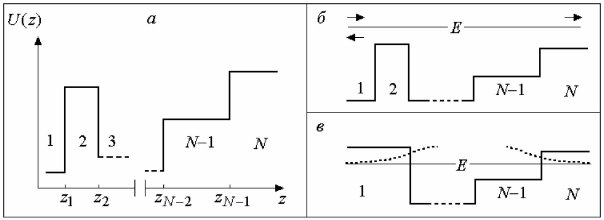
Рис. 1. К постановке задач в методе матриц переноса

В каждом слое решение уравнения Шредингера представляется в форме , где двумерный волновой вектор K, параллельный плоскости слоев, не зависит от номера слоя n, а функция от слоя к слою изменяется и в общем случае имеет вид суммы двух экспонент:

(1)

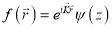
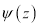
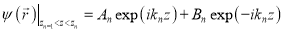
В этом выражении kn есть z-компонента волнового вектора электрона:

(2)

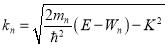
где mn и Wn — значения эффективной массы электрона и потенциала U(z) в слое с номером n. Мы будем считать, как и выше, что при извлечении квадратного корня (2) из положительной величины берется положительное значение корня, а в случае отрицательной величины под корнем волновой вектор kn становится мнимым с положительной мнимой частью: При таком выборе знака корня экспонента с коэффициентом An в случае мнимого волнового вектора kn становится убывающей функцией аргумента z, а экспонента с коэффициентом Bn — возрастающей функцией.

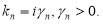
Пусть волновая функция удовлетворяет граничным условиям типа в каждой точке z = zn:

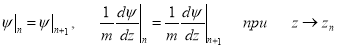
Отсюда следуют равенства

(3)

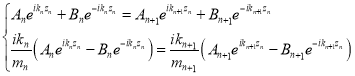
связывающие друг с другом пары коэффициентов A _n , Bn и A _{n +1} , Bn+1.

Существуют различные формулировки метода матриц переноса, поскольку можно рассматривать связь не только между указанными парами коэффициентов, но и между линейными комбинациями этих величин. Ниже речь идет о варианте, в котором вектор-столбец

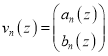
в любом слое n строится из функций

(4)

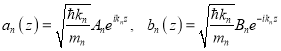
Мы будем прослеживать перенос граничных условий справа налево, выражая с помощью t -матриц вектор-столбцы vn(z) с меньшими номерами n через величины с большими номерами.

При вещественном kn функции (4) интерпретируются как комплексные амплитуды z-составляющих потока вероятности: есть поток вдоль оси z в n-ом слое, — поток в противоположном направлении в том же слое. Часто интерес представляет вероятность D прохождения электрона сквозь всю систему слоев или вероятность R отражения от нее. Постановка такой задачи проиллюстрирована рисунком 1 б. Вероятности D и R определяются как отношения потоков вероятности

(5)

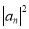
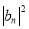
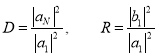
Они должны удовлетворять тождеству D + R = 1, поэтому достаточно вычислить только первую из величин (5). Предположим, что найдена матрица переноса для всей системы N слоев, то есть нам известны коэффициенты Tik в уравнениях вида

(6)

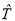
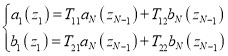
Поскольку в крайнем правом слое поток частиц в направлении, противоположном оси z, в рассматриваемой постановке задачи отсутствует, необходимо положить . При этом из уравнений (5)–(6) следуют соотношения, связывающие искомые вероятности D и R непосредственно с элементами матрицы :

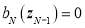
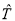
Для состояний с дискретным спектром энергии E (при фиксированном K) вероятности D и R теряют смысл; новая постановка задачи показана на рис. 1 в. В этих состояниях и , поэтому первое из уравнений (6) сводится к условию , где . Следовательно, дисперсионное уравнение для размерно-квантованных уровней энергии En(K) может быть записано в виде

(7)

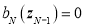
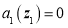
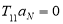
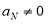
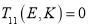
Формулы (6)–(7) показывают, что знание матрицы

дает нам много полезной информации об электронных состояниях в слоистой наноструктуре.

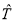
Перейдем к вычислению T-матрицы. Сначала найдем матрицу , связывающую соседние вектор-столбцы vn и vn+1 в точке z=zn:

(8)

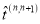
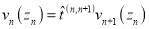
Заметим, что с учетом определений (4) уравнения (3) можно переписать в виде:

,(9)

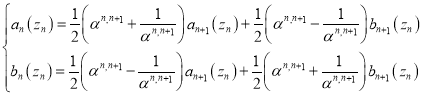
где введено обозначение

(10)

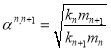
Коэффициенты в уравнениях (9) и являются элементами матрицы

(11)

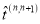
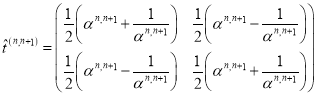
Отметим, что определитель матрицы (11) равен единице, а обратная матрица может быть получена заменой в (11) величин на , так что:

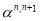
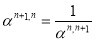
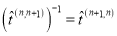
Кроме того, нам потребуется матрица , связывающая вектор-столбцы на границах одного и того же слоя:

(12)

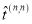
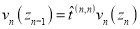
Из выражений (4) видно, что

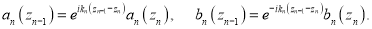
Следовательно,

(13)

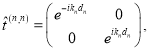
где есть толщина n-го слоя. Определитель матрицы (13) также равен единице. Обратная матрица может быть получена заменой dn на — dn. Теперь, последовательно выражая вектор-столбцы v _n (z) с меньшими номерами через вектор-столбцы с большими номерами в соответствующих граничных точках zn, мы придем к соотношению

(14)

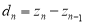
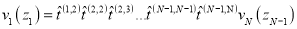
эквивалентному уравнениям (6). Таким образом, искомая T-матрица равна произведению t-матриц типа (11) и (13):

(15)

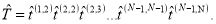
Определитель T-матрицы равен единице, поскольку равны единице определители каждого матричного сомножителя в (15); такие матрицы называются унимодулярными.

Литература:

1. Material’s electronic structure / B. B. Akhmedov, J. Y. Rozikov, I. A. Muminov. — Текст: непосредственный // Zbiór artykułów naukowych recenzowanych. — Barcelona: Diamond trading tour, 2019. — С. 78–80.
2. Dimensionally quantized semiconductor structures / B. B. Akhmedov, J. Y. Rozikov, I. A. Muminov, V. U. Ruziboev. — Текст: непосредственный // Scientific Bulletin of Namangan State University. — 2019. — № 6. — С. 58–63.
3. Метод kp-возмущений с учетом вырождения / Б. Б. Ахмедов, Ж. Ю. Розиков, А. И. Зокиров, В. У. Рузибоев. — Текст: непосредственный // Наука и современное общество: актуальные вопросы, достижения и инновации. — Пермь: НАУКА и просвещение, 2020. — С. 21–25.
4. Уравнение Шредингера для волновых функций блоха / Б. Б. Ахмедов, Ж. Ю. Розиков, А. И. Зокиров, В. У. Рузибоев. — Текст: непосредственный // Научный форум: технические и физико-математические науки. — Пермь: НАУКА и просвещение, 2020. — С. 20–25.
5. About wavefunctions in low-dimensional semiconductors / B. B. Akhmedov, J. Y. Rozikov, I. A. Muminov, V. U. Ruziboev. — Текст: непосредственный // Central Asian Problems of Modern Science and Education. — 2018. — № 4. — С. 51–57.