Цель статьи — точного решения задачи Коши для уравнения Шредингера с квадратичным гамильтонианом для заряженной частицы, в электрическом поля с компонентами (E1,E2) и магнитном поле H. Вектор H перпендикулярен вектору электрического поля (E1,E2).
Ключевые слова: гамильтониан, канонические преобразования, сжатые состояния.
Задача о вычислении точных решений уравнения Шредингера имеет важное значение в современной квантовой физике. Ряд актуальных задач квантовой оптики и квантовой теории информации описывается многомодовыми квадратичным гамильтонианом вида:
![]() (1)
(1)
В настоящее время существуют различные методы построения решений уравнения Шредингера с гамильтонианом вида (1), к которым можно отнести: метод диагонализации Боголюбова, метод Вея-Нормана, метод функции Грина и др. Каждый из вышеперечисленных методов обладает своими преимуществами и недостатками. Не останавливаясь подробно на каждом, отметим лишь основные трудности, возникающие при применении этих методов.
– Метод диагонализации Боголюбова — метод линейной диагонализации не всегда осуществим.
– Метод Вея-Нормана — не гарантируется существования решения. [8]
– Метод функции Грина связан с трудностями приведения к нормальной упорядоченной форме оператора эволюции.
В настоящей работе для решения задач Коши для уравнения Шредингера с Гамильтонианом вида (1) используется метод Канонических преобразований. Интерес к этому методу также связан с тем, что сжатые состояния, порождаемые оператором ![]() , являются инструмент для оценок чувствительности физических приборов. В частности, в работах Д. Холленхорстом (J. Hollenhorst) и К. Кейвсом (C. Caves) рассматриваются возможности квантовых измерений для обнаружения гравитона. В последнее время особый интерес к теме сжатых состояний связан с изучением теории квантовой запутанности, которое играет существенную роль в проектах создания квантового компьютера.
, являются инструмент для оценок чувствительности физических приборов. В частности, в работах Д. Холленхорстом (J. Hollenhorst) и К. Кейвсом (C. Caves) рассматриваются возможности квантовых измерений для обнаружения гравитона. В последнее время особый интерес к теме сжатых состояний связан с изучением теории квантовой запутанности, которое играет существенную роль в проектах создания квантового компьютера.
Ниже рассматриваются алгоритмы точного решения задачи Коши для уравнения Шредингера с квадратичным гамильтонианом для заряженной частицы, в электрическом поля с компонентами (E1,E2) и магнитном поле H. Вектор H перпендикулярен вектору электрического поля (E1,E2).
Аналитическое решение задачи о квантовой эволюции в скрещенных электромагнитных полях
Рассмотрим гамильтониан
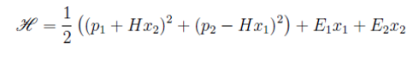 (2)
(2)
Данный H гамильтониан описывает заряженную частицу без учета спина в скрещенных однородном электрическом и магнитном полях. Плоскость действия электрического поля с компонентами (E1,E2) перпендикулярна направлению действия магнитного поля H см. (2). Для упрощения обозначений, уравнение Шредингера написано в предположении, что m = 1, c = 1, e = 1.
Алгоритм решения:
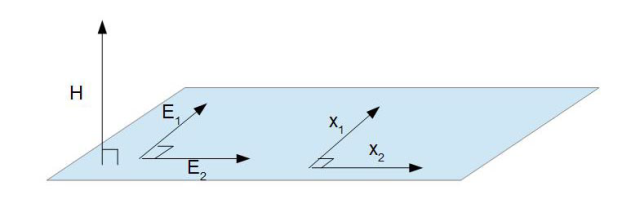
Рис. 1. Схематическое расположение электрического (E1,E2) магнитного поля H
- С помощью преобразований
![]()
привести гамильтониан с координатно-импульсного представления в представление вторичного квантования. Нахождение матриц A и B.
- С помощью найденных матриц A, B и преобразования
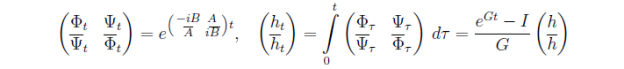 найти матрицы Ψ и Φ.
найти матрицы Ψ и Φ.
- Используя найденные матрицы Ψ,Φ и выражения [1]
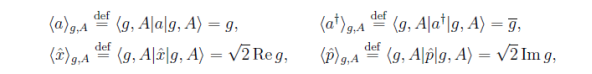
найти значения координат и импульса в зависимости от значения магнитного поля H и времени t.
- Построить графики зависимости координаты и импульса x(t,h)(1,1) p(t)(1,1) от времени t и значений магнитного поля H.
Для нахождения матриц A,B подставим величины
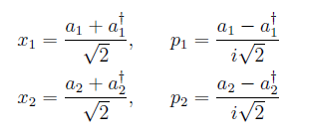 (3)
(3)
в гамильтониан (2). Учитывая, что
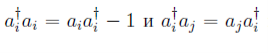
перепишем его в виде
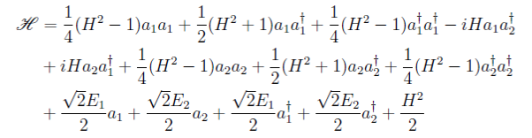 (4)
(4)
отсюда сопоставляя (4) с
![]()
находим
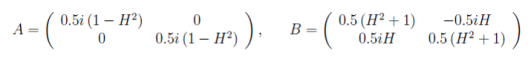 (5)
(5)
Также находим
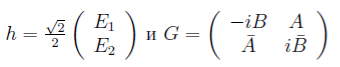
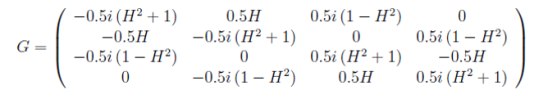 (6)
(6)
Аналитическое представление матрицы Ψ и Φ через элементарные функции в общем случае невозможно, поскольку для этого необходимо решить характеристическое уравнение степени 2n для n-мерных задач.
Метод решения задачи с помощью уравнения Гамильтона
Вернемся к рассмотрению ранее упомянутого гамильтониана
![]()
с помощью уравнения Гамильтона
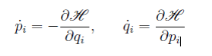 (7)
(7)
Где pi = (p1, p2,..., p𝑁) — обобщенные импульсы, q𝑖 = (q1, q2,..., q𝑁) — обобщенные координаты, Η — функция Гамильтона, получим следующие выражения
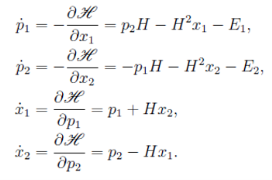 (8)
(8)
Введем вектор неизвестных Z = {x1, x2, p1, p2} и перепишем неравенство (8) в матричном виде
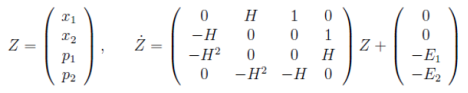 (9)
(9)
Мы получили линейную неоднородную систему дифференциальных уравнений первого порядка общее решение Zg которого можно представить как сумму общего решение однородной части Zgu и частного решения Zp.
![]() (10)
(10)
Найдем общего решение однородной части Zgu и применяя обозначение для G, запишем однородную систему в более компактной форме
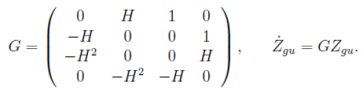 (11)
(11)
После элементарных преобразований получаем
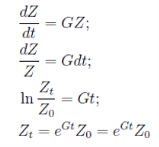 (12)
(12)
явный вид ![]() находиться методом матричной экспоненты и имеет следующий вид
находиться методом матричной экспоненты и имеет следующий вид
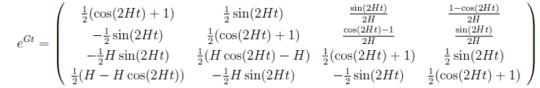 (13)
(13)
решая обратную задачу
![]() (14)
(14)
аналогичным образом получаем
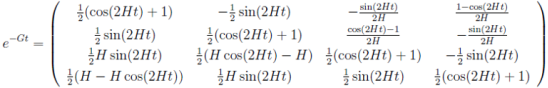 (15)
(15)
Для нахождения частного решения воспользуемся следующими обозначениями
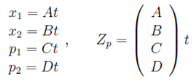 (16)
(16)
подставляя данные величины в (8) и решая систему алгебраических уравнений, находим частное решение Zp
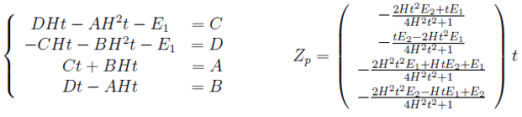 (17)
(17)
Таким образом, общее решение систему дифференциальных уравнений Zg можно записать в виде
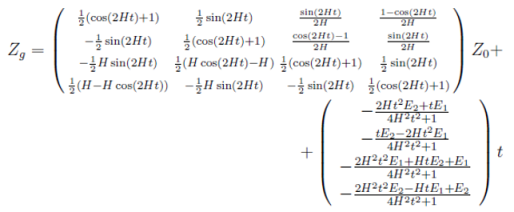 (18)
(18)
где Z0-значение вектора Z в момент времени t = 0.
Явный вид матриц Ψ и Φ в этом методе можно получить, если сравнить формулу [2]
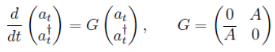
с формулой (12) и обратные соотношения к (3), которые имеют следующий вид
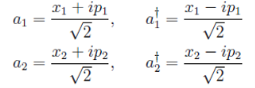 (19)
(19)
таким образом, получаем
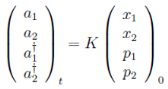 (20)
(20)
где матрица K имеет вид
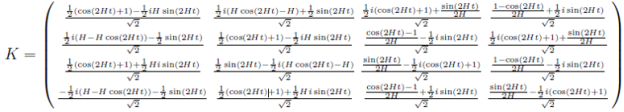 (21)
(21)
также не сложно из соотношений (3) определить матрицу перехода от начального вектора из координатно-импульсного представления в представлении вторичного квантования
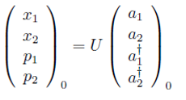 (22)
(22)
где матрица перехода U имеет вид
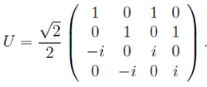 (23)
(23)
таким образом, подставляя (22) в (20) получаем
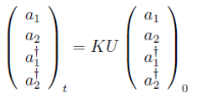 (24)
(24)
сравнивая выражения [3]
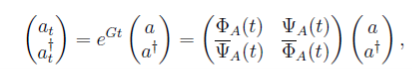
c выражением (28), получаем
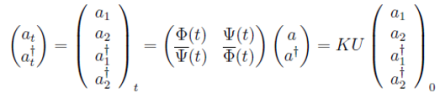 (25)
(25)
производя матричное произведение KU, мы можем получить аналитическое выражение для компонент матриц Ψ и Φ
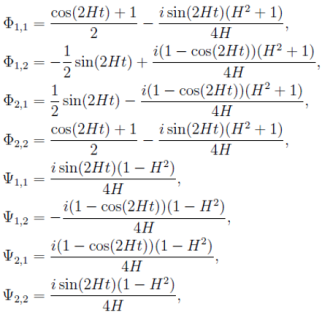 (26)
(26)
Метод решения задачи с помощью матриц канонических преобразований
Продолжим рассмотрение ранее упомянутого гамильтониана
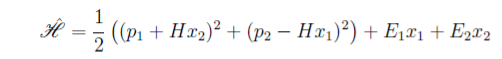
Для нахождения матриц A,B подставим величины
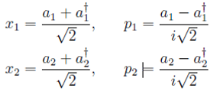 (27)
(27)
в гамильтониан (2). Учитывая, что
![]()
перепишем его в виде
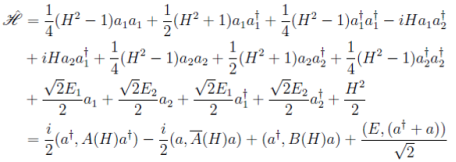 (28)
(28)
отсюда сопоставляя (28) с выражением [6]
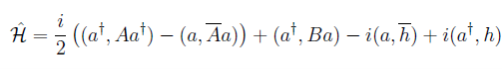
находим
![]() (29)
(29)
также находим
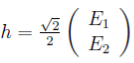
Для нахождения матриц Ψt и Φt воспользуемся уравнением Гейзенберга для операторов рождения-уничтожения
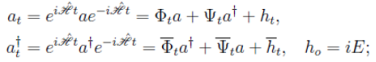 (30)
(30)
получим
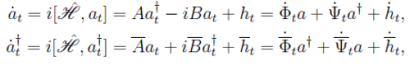 (31)
(31)
решая совместно (30) и (31) получаем
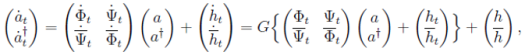 (32)
(32)
далее интегрируя данное выражение, получаем
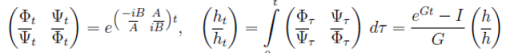 (33)
(33)
поскольку матрицы A, B и вектор h известны, то решая методом матричной экспоненты уравнение (32) мы можем получить явные представления функций Ψt и Φt и вектора ht
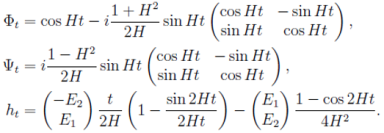 (34)
(34)
Для того, чтобы получить зависимость координаты и импульса заряженной частицы от времени и значений магнитного и электрического полей, подставим соотношения (30) в (27)
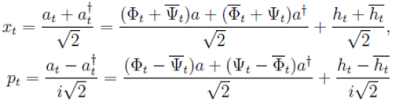 (35)
(35)
где
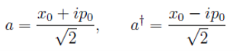 (36)
(36)
в котором
![]()
значение координат и импульса в начальный момент времени.
Подставляя матрицы Ψt и Φt из (34) в (35) получаем
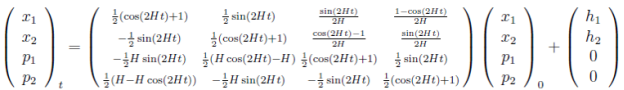 (37)
(37)
где
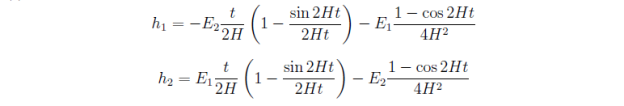
Отметим, что для линейных членов
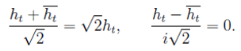 (38)
(38)
так как вектор
![]()
По найденным выражениям построим графики среднего значения координаты и импульса в зависимости от времени t и значения магнитного поля H.
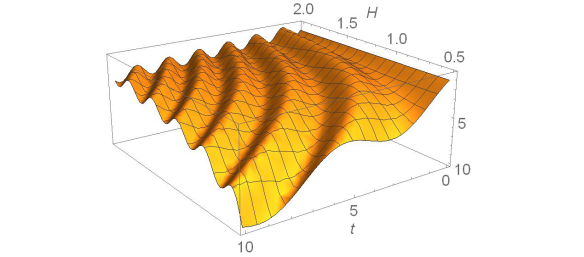
Рис. 2. График зависимости среднего значения координаты x1 (H,t) от времени t и значения магнитного поля H
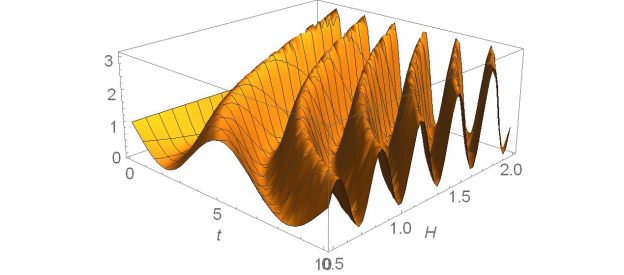
Рис. 3. График зависимости среднего значения импульса p1 (H,t) от времени t и значения магнитного поля H.
Литература:
- Чеботарев, А. М. Сжатые состояния и их применение в задачах квантовой эволюции / А. М. Чеботарев, Т. В. Тлячев, А. А. Радионов // Математические заметки. — 2011. — Т. 89. — С. 614–634.
- Чеботарев, А. М. Обобщенные сжатые состояния и многомерная формула факторизации / А. М. Чеботарев, Т. В. Тлячев, А. А. Радионов // Математические заметки. — 2012. — Т. 92. — С. 762–777.
- Chebotarev, A. M. Lectures on quantum probability / A. M. Chebotarev. — Sociedad: Mathematica Mexicana, 2000. — 305 p
- Tlyachev, T. V. A new approach to quantum theory of multimode coupled parametric processes / T. V. Tlyachev, A. M. Chebotarev, A. S. Chirkin // Physica Scripta –2013. — V. T153. — 014060.
- Chebotarev, A. M. Normal Forms, Inner Products, and Maslov Indices of General Multimode Squeezings / A. M. Chebotarev, T. V. Tlyachev // Mathematical Notes.– 2014. –Vol. 95- No. 5 — pp. 721–737.
- R. P. Feynman, “An operator calculus having application in quantum electrodynamics,” Phys. Rev. 84 (1), 108–128 (1951).
- F. A. Berezin, The Method of Second Quantization (New York, 1966).
- Wei, J. Lie algebraic solution of linear differential equations / J. Wei, E. Norman //J. Math. Phys. — 1963. — V. 4. — P. 575–581.
- А. В. Поляков, А. М. Чеботарев, “Метод Монте-Карло для уравнения Шрёдингера с периодическим асимметричным потенциалом”, Ж. вычисл. матем. и матем.физ., 44:10 (2004), 1898–1908.

